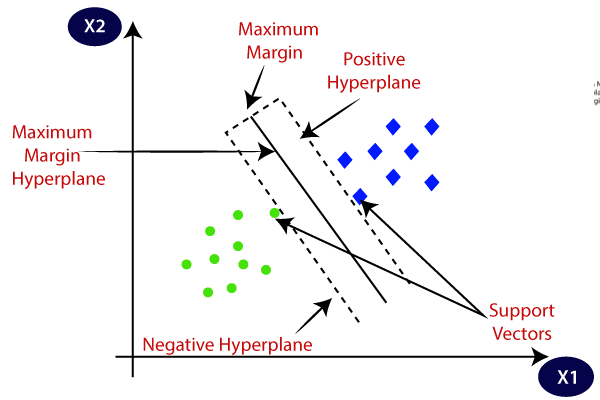
Support Vector Machine sau SVM este unul dintre cei mai populari algoritmi de învățare supravegheați, care este utilizat pentru clasificare, precum și pentru probleme de regresie. Cu toate acestea, în primul rând, este utilizat pentru probleme de clasificare în învățarea mașinilor.scopul algoritmului SVM este de a crea cea mai bună linie sau limită de decizie care poate separa spațiul n-dimensional în clase, astfel încât să putem pune cu ușurință noul punct de date în categoria corectă în viitor., Această limită cea mai bună decizie se numește un hyperplane.SVM alege punctele/vectorii extreme care ajută la crearea hyperplanului. Aceste cazuri extreme sunt numite vectori de suport și, prin urmare, algoritmul este denumit mașină Vector de suport. Considerăm diagrama de mai jos în care există două categorii diferite, care sunt clasificate folosind o decizie limita sau hiperplan:
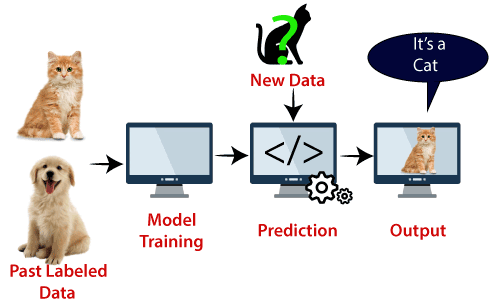
Exemplu: SVM poate fi înțeleasă cu exemplul pe care l-am folosit în clasificatorul KNN., Să presupunem că vedem o pisică ciudată care are și unele caracteristici ale câinilor, deci dacă dorim un model care să poată identifica cu exactitate dacă este o pisică sau un câine, un astfel de model poate fi creat folosind algoritmul SVM. Mai întâi vom antrena modelul nostru cu o mulțime de imagini cu pisici și câini, astfel încât să poată învăța despre diferite caracteristici ale pisicilor și câinilor, apoi îl testăm cu această creatură ciudată. Deci, ca vector de sprijin creează o limită de decizie între aceste două date (pisică și câine) și alege cazuri extreme (vectori de sprijin), se va vedea cazul extrem de pisică și de câine., Pe baza vectorilor de sprijin, o va clasifica ca o pisică. Luați în considerare diagrama de mai jos:
algoritmul SVM poate fi utilizat pentru detectarea feței, clasificarea imaginilor, clasificarea textului etc.
tipuri de SVM
SVM poate fi de două tipuri:
- SVM liniar: SVM liniar este utilizat pentru date separabile liniar, ceea ce înseamnă că dacă un set de date poate fi clasificat în două clase folosind o singură linie dreaptă, atunci aceste date sunt denumite date separabile liniar, iar clasificatorul este utilizat ca clasificator SVM liniar.,
- SVM neliniar: SVM neliniar este utilizat pentru date separate neliniar, ceea ce înseamnă că dacă un set de date nu poate fi clasificat folosind o linie dreaptă, atunci aceste date sunt denumite date neliniare, iar clasificatorul utilizat este numit clasificator SVM neliniar.
Hiperplan și Sprijin Vectori în algoritmul SVM:
Hiperplan: pot Exista mai multe linii/decizia de limite pentru a separa clasele în n-dimensională de spațiu, dar trebuie să găsim cea mai bună decizie de frontieră, care vă ajută pentru a clasifica datele de puncte. Această limită cea mai bună este cunoscută sub numele de hyperplanul SVM.,
dimensiunile hiperplan depinde de caracteristicile prezente în setul de date, ceea ce înseamnă că dacă există 2 caracteristici (așa cum se arată în imagine), apoi hiperplan va fi o linie dreaptă. Și dacă există 3 caracteristici, atunci hyperplanul va fi un plan cu 2 dimensiuni.întotdeauna creăm un hyperplan care are o marjă maximă, ceea ce înseamnă distanța maximă dintre punctele de date.
vectorii de suport:
punctele de date sau vectorii care sunt cei mai apropiați de hyperplan și care afectează poziția hyperplanului sunt numiți vectori de suport., Deoarece acești vectori susțin hyperplane, prin urmare, numit un vector de sprijin.
cum acționează SVM?
Linear SVM:
funcționarea algoritmului SVM poate fi înțeleasă folosind un exemplu. Să presupunem că avem un set de date care are două etichete (verde și albastru), iar setul de date are două caracteristici x1 și x2. Ne dorim un clasificator care poate clasifica perechea (x1, x2) de coordonate în verde sau albastru. Luați în considerare imaginea de mai jos:
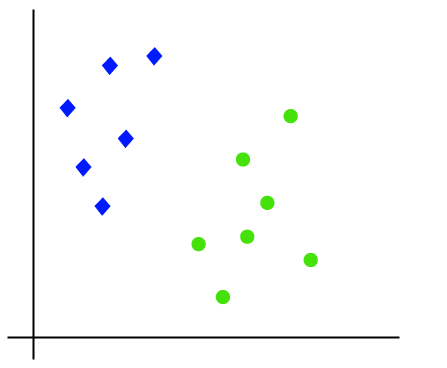
deci, deoarece este spațiu 2-d, Deci folosind doar o linie dreaptă, putem separa cu ușurință aceste două clase., Dar pot exista mai multe linii care pot separa aceste clase. Luați în considerare imaginea de mai jos:
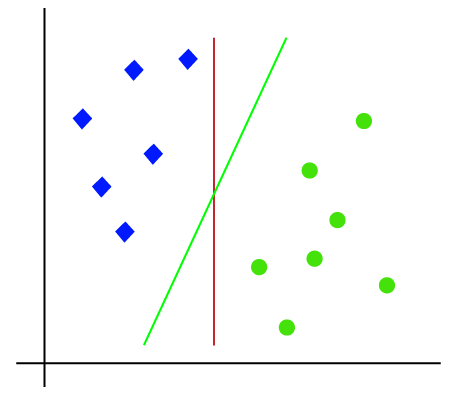
prin Urmare, algoritmul SVM vă ajută să găsiți cea mai bună linie sau decizie limită; acest cel mai bun de frontieră sau regiune este numit ca un hiperplan. Algoritmul SVM găsește cel mai apropiat punct al liniilor din ambele clase. Aceste puncte se numesc vectori de sprijin. Distanța dintre vectori și hiperplan este numită marjă. Iar scopul SVM este de a maximiza această marjă. Hyperplanul cu marjă maximă se numește hyperplanul optim.,
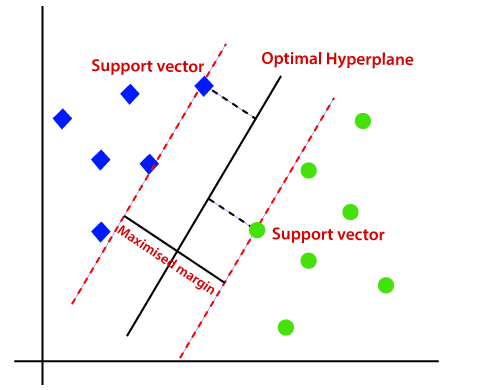
SVM neliniar:
dacă datele sunt aranjate liniar, atunci le putem separa folosind o linie dreaptă, dar pentru datele neliniare, nu putem desena o singură linie dreaptă. Luați în considerare imaginea de mai jos:
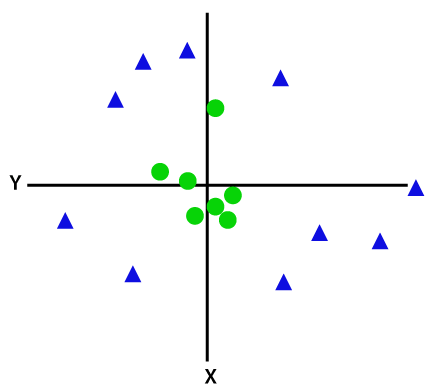
deci, pentru a separa aceste puncte de date, trebuie să adăugăm încă o dimensiune. Pentru datele liniare, am folosit două dimensiuni x și y, astfel încât pentru datele neliniare, vom adăuga o a treia dimensiune z., Acesta poate fi calculat ca:
z=x2 +y2
Prin adăugarea a treia dimensiune, proba spațiu va deveni ca imaginea de mai jos:
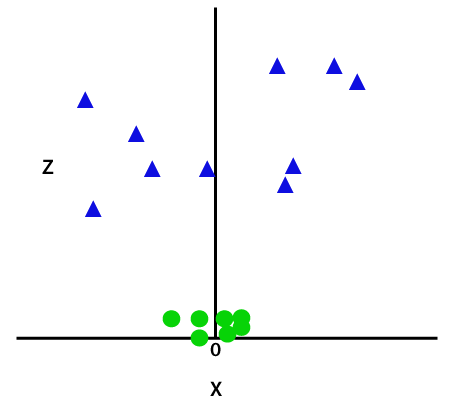
Deci, acum, SVM va împărți seturi de date în clase în felul următor. Luați în considerare imaginea de mai jos:
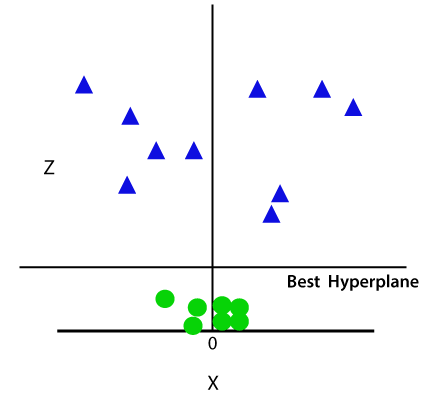
deoarece suntem în spațiul 3-d, prin urmare, arată ca un plan paralel cu axa X. Dacă îl convertim în spațiu 2D cu z=1, atunci va deveni ca:
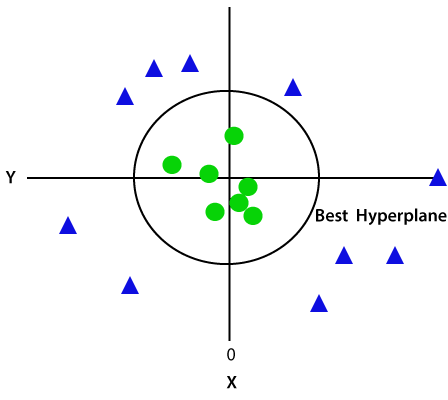
prin urmare, obținem o circumferință a razei 1 în cazul datelor neliniare., implementarea Python a mașinii vector de suport acum vom implementa algoritmul SVM folosind Python. Aici vom folosi același set de date user_data, pe care l-am folosit în regresia logistică și clasificarea KNN.
- etapa de Pre-procesare a datelor
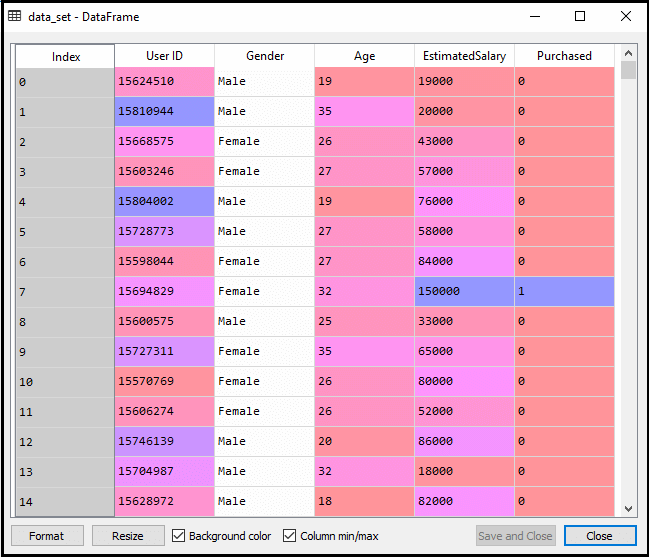
până la etapa de pre-procesare a datelor, codul va rămâne același. Mai jos este codul:
după executarea codului de mai sus, vom pre-procesa datele., Codul va oferi date ca:
scalate de ieșire pentru setul de testare va fi:
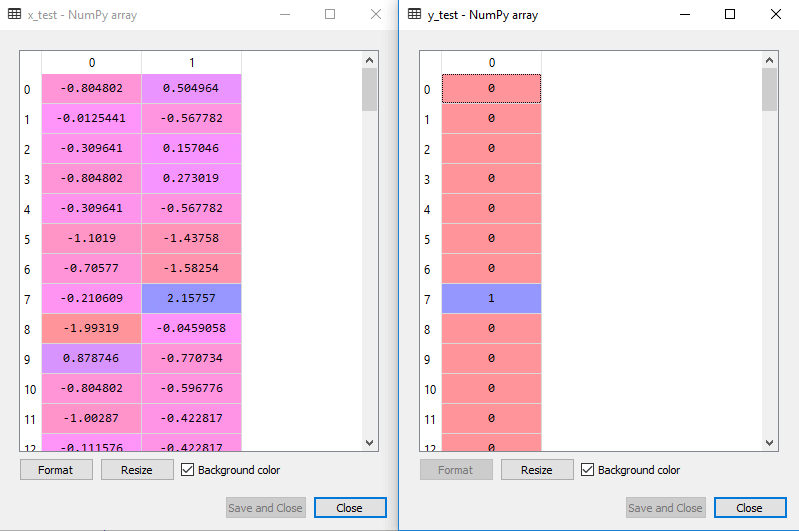
Montarea clasificator SVM pentru setul de antrenament:
Acum setul de antrenare va fi montat la clasificator SVM. Pentru a crea clasificatorul SVM, vom importa clasa SVC din Sklearn.biblioteca svm. Mai jos este codul pentru acesta:
în codul de mai sus, am folosit kernel=’linear’, deoarece aici creăm SVM pentru date separabile liniar. Cu toate acestea, îl putem schimba pentru date neliniare., Și apoi am montat clasificator la formarea set de date(x_train, y_train)
Ieșire:
modelul de performanță poate fi modificat prin schimbarea valorii C(factor de Regularizare), gamma, și kernel.
- prezicerea rezultatului setului de teste:
acum, vom prezice rezultatul pentru setul de teste. Pentru aceasta, vom crea un nou vector y_pred. Mai jos este codul pentru asta:
Dupa ce y_pred vector, putem compara rezultatul de y_pred și y_test pentru a verifica diferența între valoarea reală și a prezis valoare.,
Ieșire: mai Jos este de ieșire pentru predicția testului set:

- Crearea de confuzie matrix:
Acum vom vedea performanța clasificatorului SVM, care cât de multe predictii incorecte sunt acolo comparativ cu regresia Logistică clasificator. Pentru a crea matricea de confuzie, trebuie să importăm funcția confusion_matrix a Bibliotecii sklearn. După importarea funcției, o vom numi folosind o nouă variabilă cm. Funcția Are doi parametri, în principal y_true (valorile reale) și y_pred (valoarea țintă returnată de clasificator)., Mai jos este codul pentru aceasta:
Output:
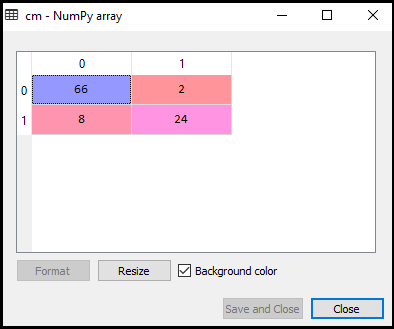
după cum putem vedea în imaginea de ieșire de mai sus, există 66+24= 90 predicții corecte și 8+2= 10 predicții corecte. Prin urmare, putem spune că modelul nostru SVM îmbunătățit în comparație cu modelul de regresie logistică.,
- Vizualizarea de formare a stabilit rezultatul:
Acum vom vizualiza setul de instruire urmare, mai jos este codul pentru asta:
Ieșire:
Prin executarea codului de mai sus, vom obține de ieșire ca:
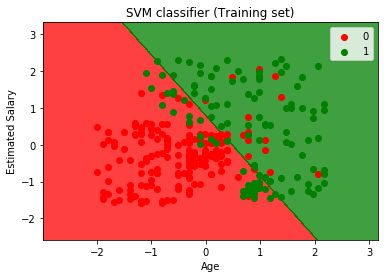
după Cum putem vedea, mai sus de ieșire apare similare la regresie Logistică ieșire. În ieșire, am obținut linia dreaptă ca hyperplane, deoarece am folosit un kernel liniar în clasificator. Și am discutat mai sus că pentru spațiul 2D, hyperplanul din SVM este o linie dreaptă.,
- pentru a vizualiza setul de testare rezultat:
Ieșire:
Prin executarea codului de mai sus, vom obține de ieșire ca:
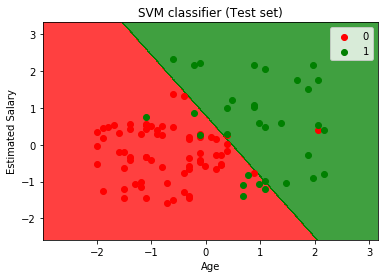
după Cum putem vedea în cele de mai sus a imaginii de ieșire, clasificator SVM a împărțit utilizatorii în două regiuni (Cumpărate sau achiziționate). Utilizatorii care au achiziționat SUV-ul se află în regiunea roșie cu punctele scatter roșu. Și utilizatorii care nu au achiziționat SUV-ul se află în regiunea verde cu puncte de împrăștiere verzi. Hyperplanul a împărțit cele două clase în variabile achiziționate și nu achiziționate.