unul dintre cele mai mari aspecte ale Sudoku este că jocul oferă provocări angajarea atât novice, precum și jucătorul puzzle condimentată. Ori de câte ori joacă un puzzle adaptat pentru nivelul lor de competență, atât începătorul, cât și solverul Sudoku experimentat vor trebui să pună o cantitate bună de gândire și tehnică în finalizarea sarcinii. Abordarea lor, deși, nu poate fi același lucru. Rezolvarea unui puzzle greu Sudoku va necesita destul de un set diferit de tehnici, comparativ cu unul ușor., Acest articol prezintă nouă astfel de tehnici; în dificultate în creștere.
atunci când se utilizează aceste tehnici, modul în care profesioniștii preferă să o facă, este de a începe cu cele de bază. Utilizați primele câteva tehnici pentru a insera cât mai multe numere ca tine poate. Apoi, când nu mai puteți adăuga numere la bord folosind tehnicile de bază, încercați cele mai avansate. Faceți unul câte unul până când puteți complot încă un număr într-o celulă. Apoi, începeți din nou cu tehnicile de bază și repetați procesul. Ar trebui să puteți rezolva aproape orice puzzle Sudoku folosind aceste tehnici.,

tehnici pentru eliminarea numerelor:

candidat unic

când o anumită celulă poate conține doar un singur număr, acel număr este un „candidat unic”. Acest lucru se întâmplă ori de câte ori toate celelalte numere, dar numărul candidatului există fie în blocul curent, coloană sau rând. În acest exemplu, celula roșie poate conține doar numărul 5, deoarece celelalte opt numere au fost utilizate în blocul, coloana și rândul aferent.,

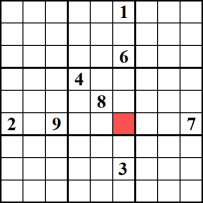
Candidat Unic

știi că fiecare bloc, de rând și de coloană pe un Sudoku bord trebuie să conțină fiecare număr între 1 și 9. Prin urmare, dacă un număr, să zicem 4, poate fi pus într-o singură celulă dintr-un bloc/coloană/rând, atunci acel număr este garantat să se potrivească acolo. Acest exemplu ilustrează numărul 4 ca candidat unic pentru celula marcată cu roșu.,

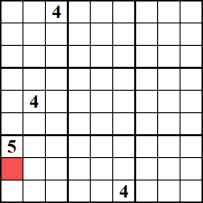
Tehnici pentru eliminarea candidaților:

Bloc și coloană / Rând Interacțiune

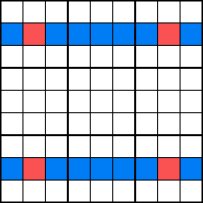
Această metodă nu te va ajuta creion în orice numere noi, dar aceasta vă va ajuta unghii un număr în jos într-un anumit rând sau coloană. Exemplul arată că numărul 7 poate fi introdus numai în celulele roșii ale rândului din mijloc. Astfel, puteți elimina 7 ca posibil candidat din restul rândului.,

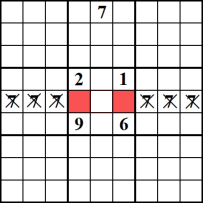
Bloc / Bloc de Interacțiune

Această tehnică este cel mai bine înțeleasă de către uita la exemplu. În blocurile din mijloc și din stânga, numărul 8 trebuie plasat într-una din celulele roșii. Aceasta înseamnă că putem elimina 8 din rândurile superioare și inferioare din coloana din dreapta-mijloc.,

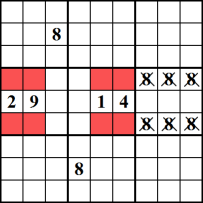
Gol Subset

De exemplu, arată că numărul de rând 1 și numărul de rând 5 ambele au o celulă în aceeași coloană conține numai candidatul numerele 4 si 7. Aceste două numere apar ca candidați în toate celelalte celule deschise din acea coloană, dar din moment ce sunt singurii doi candidați din rândurile 1 și 5, aceste două numere nu pot apărea nicăieri în altă parte a rândului, astfel le puteți elimina. În exemplu, cele două perechi de candidați încercuite în roșu, sunt singurii candidați., Deoarece 4 și 7 trebuie să fie plasate în oricare dintre aceste două celule, toate perechile încercuite în albastru, poate elimina aceste numere ca candidați. În acest puzzle, aceasta înseamnă că 1 devine candidat unic în al doilea rând; 2 devine candidat unic în rândul 6; și astfel, 6 este candidat unic pentru rândul 4.
De asemenea, puteți utiliza această tehnică dacă aveți mai mult de doi candidați. De exemplu, să spunem că perechile încercuite în roșu au fost în schimb candidați tripli ai numerelor 1, 4, 7. Acest lucru ar însemna că aceste trei numere ar trebui să fie plasate în rândurile 1, 2 sau 5., Am putea elimina aceste trei numere ca candidați în oricare dintre celulele rămase din coloană. Această tehnică funcționează chiar și cu patru numere de candidați, presupunând că aveți 4 candidați posibili în patru celule diferite într-un rând/coloană.

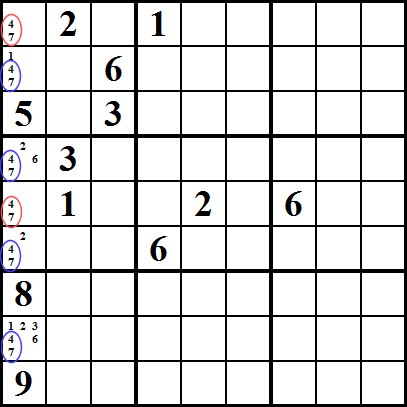
Ascuns subset

Acest lucru este similar cu Gol subset, dar nu afectează celulele care deține candidați., În acest exemplu, vedem că numerele 5, 6, 7 pot fi plasate numai în celulele 5 sau 6 din prima coloană (marcate într-un cerc roșu) și că numărul 5 poate fi introdus numai în numărul celulei 8 (marcat într-un cerc albastru). Deoarece 6 și 7 trebuie plasate într-una dintre celulele cu un cerc roșu, rezultă că numărul 5 trebuie plasat în numărul celulei 8 și astfel putem elimina orice alți candidați din celula a 8-A; în acest caz, 2 și 3.,

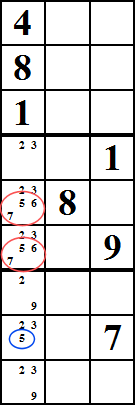
X-Wing

Această metodă se poate lucra atunci când te uiți la celulele care cuprinde un dreptunghi, astfel ca celulele marcate în roșu. În acest exemplu, să spunem că celulele roșii și albastre au toate numărul 5 ca numere candidate. Acum, imaginați-vă dacă celulele roșii sunt singurele celule din coloanele 2 și 8 în care puteți pune 5.
în acest caz, evident, trebuie să puneți un 5 în două dintre celulele roșii și, de asemenea, știți că nu pot fi ambele în același rând., Ei bine, acum, acest lucru înseamnă că puteți elimina 5 ca candidat pentru toate celulele albastre. Acest lucru se datorează faptului că în rândul de sus, fie prima, fie a doua celulă roșie trebuie să aibă un 5, și același lucru se poate spune despre rândul inferior.

Spadă

– Spadă este o versiune mai complicată a X-Wing. În cele mai multe cazuri, tehnica ar putea părea mult de lucru pentru foarte puțin salariu, dar unele puzzle-uri pot fi rezolvate numai cu ea. Deci, dacă doriți să fiți un maestru de rezolvare a sudoku, citiți mai departe!,

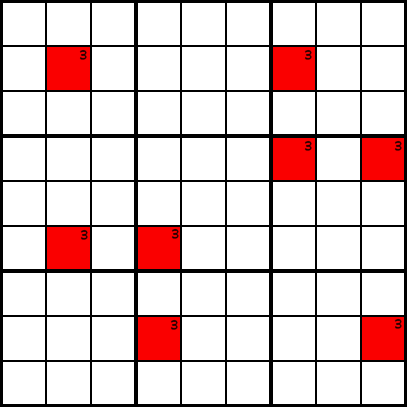Exemplu

De exemplu, am trasat în unele candidat celule pentru numărul 3. Acum, să presupunem că în coloana 2, 4, 7 și 9, singurele celule care pot conține numărul 3 sunt cele marcate cu roșu. Știți că fiecare coloană trebuie să conțină un 3.
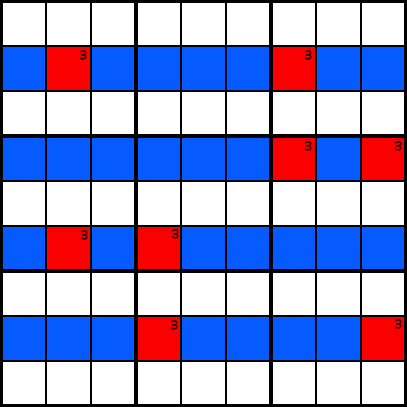Exemplu B

Uită-te la exemplul B. putem elimina 3 în calitate de candidat în fiecare celulă marcată în albastru., Motivul pentru aceasta este că, dacă luăm în considerare posibilele plasări ale numărului 3 în celulele roșii, obținem două alternative: fie trebuie să puneți 3s în celulele verzi, fie în celulele purpurii, așa cum arată exemplul C. În orice caz, fiecare dintre coloanele 2, 4, 7 și 9 trebuie să conțină un 3 într-una dintre celulele colorate, astfel încât nicio altă celulă din acele rânduri nu poate conține un 3.
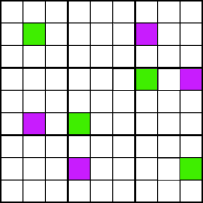Exemplu C

Cum recunoști un pește-spadă model? Căutați celule cu numere comune de candidați care pot fi înlănțuite împreună ca în exemplul D., Dacă începeți, să zicem, celula roșie din stânga sus. Apoi trageți o linie fie vertical, fie orizontal până când ajungeți la o altă celulă care conține același număr de candidat. Apoi repetați acest model până când reveniți la celula originală. Dacă ajungeți la celula originală, aveți un model de pește-spadă!
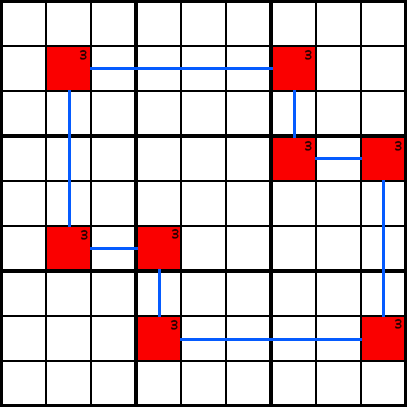Exemplu D

Forțând Lanț

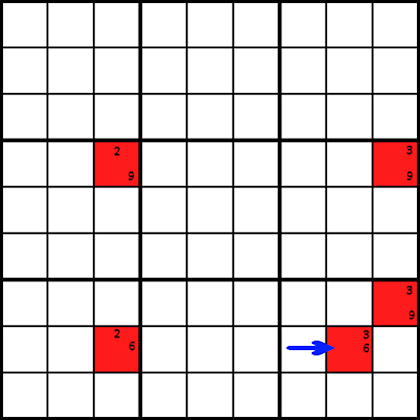
Forțând lanț de fapt vă poate ajuta să determina exact ceea ce un anumit număr de celule trebuie să dețină. Din păcate, tehnica nu este cea mai ușoară de utilizat., Uită-te la exemplul de mai jos. Să presupunem că candidații din celulele roșii sunt singurii candidați pentru aceste celule.
forțarea lanțurilor funcționează în felul următor: începeți pe celula roșie cu săgeata îndreptată spre ea și completați unul dintre cei doi candidați, 3 sau 6, pentru acea celulă. Apoi urmați și completați restul celulelor roșii. Acum luați notă de valorile pe care le introduceți pe parcurs. Du-te înapoi la celula cu care ai început și încearcă celălalt număr de candidat pentru acea celulă și completează și celelalte celule roșii. Comparați numerele pe care le-ați obținut acum cu primul rezultat., Puteți constata că, în ambele cazuri, o anumită celulă trebuie să conțină un anumit număr.
în acest exemplu, dacă puneți numărul 3 în celula de pornire, veți vedea că celula vecină din dreapta sus trebuie să conțină un 9. Acum, încercați să introduceți un 6 în celula de pornire și să mutați invers, introducând valorile candidatului. Când ajungeți din nou la celula vecină de mai sus, veți găsi că trebuie să conțină și un 9 de data aceasta. Astfel, această celulă trebuie să conțină un 9.


Asta e., Sper că acest lucru vă va ajuta să sparge chiar și cele mai dificile puzzle-uri sudoku acolo. Mult noroc!
acest articol este o parte din secțiunea noastră de ajutor Sudoku.Sudoku Epic este un joc Sudoku gratuit, de calitate premium și este disponibil pe majoritatea platformelor: PC, Mac, iPhone, iPad, Android, Google Play Store și Amazon Appstore.

Ia-l!



Sudoku Epic pe Google Play
Sudoku Epic pe iPhone/iPad-ul