acesta este primul dintr-o serie de trei posturi. Al doilea post vorbește desprecum se calculează Big-O. al treilea articol vorbește despre înțelegerea definiției formale a Big-O.
notația Big-o a fost un concept cu adevărat înfricoșător pentru mine. M-am gândit că așa au vorbit programatorii „reali” despre codul lor. Totul a fost mai înfricoșător, deoarece descrierile academice (cum ar fi Wikipedia) mi-au făcut foarte puțin sens. Acest lucru este frustrant, deoarece underlyingconcepts nu sunt de fapt atât de greu.,mai simplu spus, notația Big-O este modul în care vorbesc programatoriialgoritmi. Algoritmii sunt un alt subiect înfricoșător pe care îl voi acoperi înun alt post, dar pentru scopurile noastre, să spunem că „algoritmul” înseamnă o funcție în programul dvs. (care nu este prea departe). O funcție de mare Onotation este determinată de modul în care răspunde la diferite intrări. Cummult mai lent este dacă îi dăm o listă de 1000 de lucruri pentru a lucraîn loc de o listă de 1 lucru?
luați în Considerare acest cod:
def item_in_list(to_check, the_list): for item in the_list: if to_check == item: return True return False
Deci, dacă vom apela această funcție ca item_in_list(2, ), acesta trebuie să fie destul de rapid., Am buclă peste fiecare lucru din listă și dacă găsimprimul argument al funcției noastre, returnează True. Dacă ajungem la sfârșitși nu am găsit-o, întoarce-te fals.
„complexitatea”acestei funcții este O(n). Voi explica ce înseamnă asta într-o secundă, dar hai să descompunem această sintaxă matematică. O(n) este citit Ordinul „N” pentru că O funcția este alsoknown ca funcția de Comandă. Cred că acest lucru se datorează faptului că facemaproximație, care se ocupă de „ordine de mărime”.,
„ordine de mărime” este încă un alt termen matematic careîn principiu, spune diferența dintre clasele de numere. Gândiți-vă diferența dintre 10 și 100. Dacă vă imaginați 10 dintre cei mai apropiați prieteni și 100 de persoane, aceasta este o diferență foarte mare. În mod similar, diferența dintre 1.000 și 10.000 este destul de mare (de fapt, diferența dintre o mașină junker și una ușor utilizată). Se pare că, în aproximare,atâta timp cât sunteți într-un ordin de mărime, sunteți destul de aproape., Dacă ar fi să ghicească numărul de gumballs în amachine, v-ar fi într-un ordin de mărime dacă ați spus 200gumballs. 10.000 gumballs ar fi departe.

Figura 1: o mașină gumball al cărei număr de gumballs este probabil într-un ordin de mărime de 200.
Înapoi la disecarea O(n), aceasta spune că, dacă ar fi să-grafic datănu nevoie pentru a rula această funcție cu dimensiuni diferite intrări (de exemplu, obiective 1 element, 2, 3 obiecte, etc), vom vedea că itapproximately corespunde numărului de elemente în matrice., Acesta estenumit un grafic liniar. Aceasta înseamnă că linia este în principiu dreptădacă ar fi să o grafici.
Unii dintre voi poate au prins că, dacă, în proba de cod de mai sus, ouritem fost întotdeauna primul element din listă, codul nostru ar fi reallyfast! Acest lucru este adevărat, dar Big-O se referă la cel mai rău caz aproximativperformanța de a face ceva. Cel mai rău caz pentru codul de mai sus estecă lucrul pe care îl căutăm nu este deloc în listă. (Notă: termenul matematic pentru aceasta este „limita superioară”, ceea ce înseamnă că vorbește despre limita matematică a grozăviei).,
Dacă vrei să vezi un grafic pentru aceste funcții, puteți ignora O()funcția și de a schimba variabila n pentru x. Puteți apoi să tastați thatinto Wolfram Alpha ca „plot x” care vă va arăta o diagonală. Motivul pentru care ai schimba n pentru x este că lor grafice programwants x ca nume de variabilă deoarece corespunde xaxis. Axa x din ce în ce mai mare de la stânga la dreapta corespundeoferind matrice mai mari și mai mari funcției dvs., Axa yreprezintă timpul, deci cu cât linia este mai mare, cu atât este mai lentă.
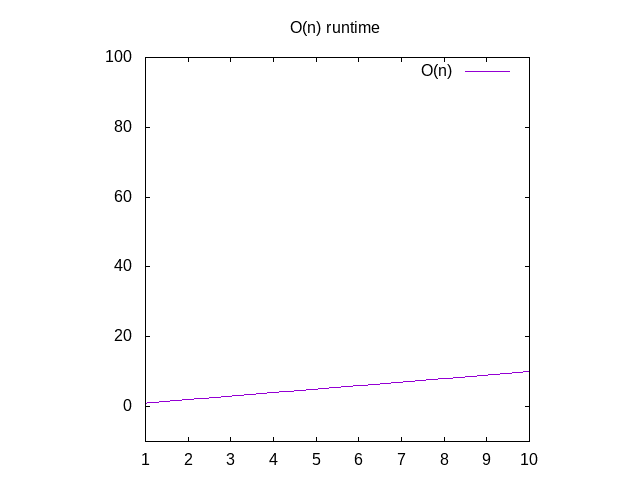
Figura 2: Caracteristicile de rulare ale unei funcții O(n)
deci, care sunt alte exemple în acest sens?
luați în considerare această funcție:
def is_none(item): return item is None
acesta este un exemplu prostesc, dar poartă cu mine. Această funcție estenumit O(1) care se numește „timp constant”. Ceea ce înseamnă asta este cât de mare este contribuția noastră, este întotdeauna nevoie de același timp pentru a calcula lucrurile., Dacă vă întoarceți la Wolfram și plot 1, veți vedea că rămâne întotdeauna la fel, indiferent cât de departe mergem. Dacă youpass într-o listă de 1 milion de numere întregi, va dura aproximativ același timpca și dacă ați fost de gând să treacă într-o listă de 1 întreg. Timpul Constant esteconsiderat cel mai bun scenariu pentru o funcție.
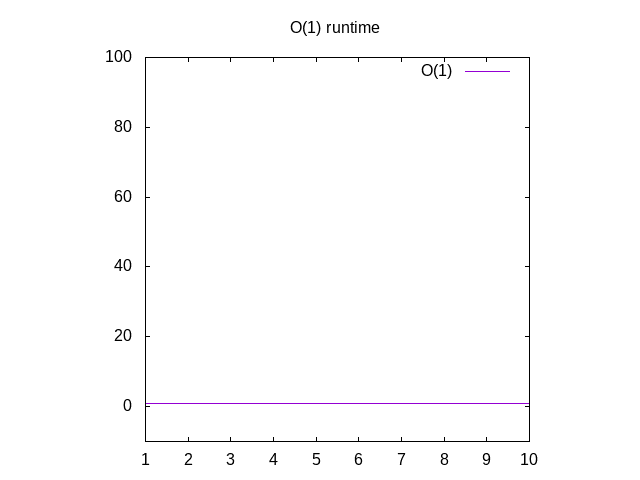
Figura 3: Runtime caracteristicile unui O(1) funcția
luați în Considerare această funcție:
mai Jos este o comparație de fiecare din aceste grafice, pentru referință., Puteți vedea că o O(n^2) funcție va primi lent foarte repede în cazul în care ca ceva care funcționează în timp constant va fi mult mai bine. Acest lucru este deosebit de util atunci când vine vorba de structuri de date, despre care voi posta în curând.
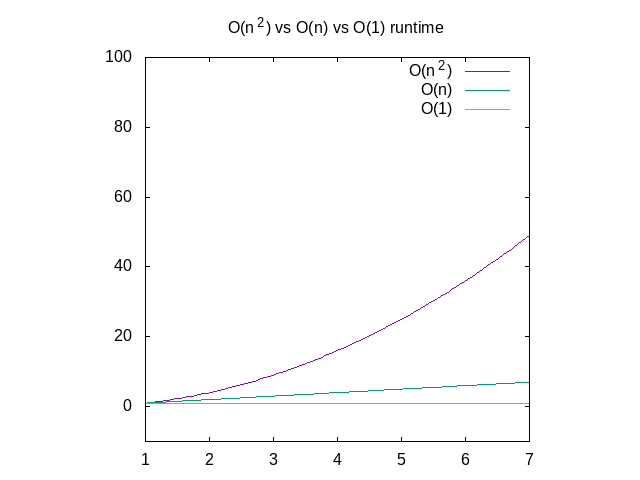
Figura 4: Comparație de O(n2) vs O(n) vs O(1) funcțiile
Acesta este un nivel destul de înalt de ansamblu de Mare-O notație, dar hopefullygets vă familiarizați cu subiectul., Există un curs de coursera care vă poate oferi o viziune mai aprofundată asupra acestui subiect, dar fiți avertizat că va intra foarte repede în notația matematică. Dacă ceva de aici nu are sens, trimite-mi un e-mail.
actualizare: am scris, de asemenea, despre cum se calculează Big-O.
mă gândesc să scriu o carte pe această temă. Dacă doriți să vedeți ceva, vă rugăm să vă exprimați interesul aici.