Ipoteza de normalitate a variabilei dependente
independente t-test impune ca variabilă dependentă este aproximativ normal distribuite în cadrul fiecărui grup.
Notă: Din punct de vedere tehnic, reziduurile trebuie distribuite în mod normal, dar pentru un test t independent, ambele vă vor oferi același rezultat.,puteți testa acest lucru folosind o serie de teste diferite, dar testul Shapiro-Wilks de normalitate sau o metodă grafică, cum ar fi un complot Q-Q, sunt foarte frecvente. Puteți rula aceste teste folosind statisticile SPSS, procedura pentru care poate fi găsită în ghidul nostru de testare pentru normalitate. Cu toate acestea, testul t este descris ca un test robust în ceea ce privește asumarea normalității. Aceasta înseamnă că o anumită abatere de la normalitate nu are o influență mare asupra ratelor de eroare de tip I. Excepția de la aceasta este dacă raportul dintre cea mai mică și cea mai mare dimensiune a grupului este mai mare de 1.,5 (cea mai mare în comparație cu cea mai mică).
Ce să fac atunci când încalcă ipoteza de normalitate a distribuției
Dacă veți găsi că una sau ambele din grupul dvs. de date nu este aproximativ normal distribuite și grupuri de dimensiuni diferă foarte mult, aveți două opțiuni: (1) transformarea datelor dvs., astfel încât datele să devină în mod normal distribuite (pentru a face acest lucru în SPSS Statistics a se vedea ghidul privind Transformarea Datelor), sau (2) executați testul Mann-Whitney U test, care este un test neparametric care nu are nevoie de ipoteza de normalitate (pentru a rula acest test în SPSS Statistics a se vedea ghidul nostru pe Mann-Whitney U Test).,
ipoteza omogenității varianței
testul t independent presupune că variațiile celor două grupuri pe care le măsurați sunt egale în populație. Dacă variațiile dvs. sunt inegale, acest lucru poate afecta rata de eroare de tip I. Ipoteza omogenității varianței poate fi testată folosind testul Levene de egalitate a varianțelor, care este produs în statisticile SPSS atunci când se execută procedura independentă de testare T., Dacă ați rulat Testul lui Levene de Egalitate a Varianțelor în SPSS Statistics, veți obține un rezultat similar cu cel de mai jos:

Acest test de omogenitate a varianței oferă un F-statistic și o valoare semnificație (p-value). Suntem preocupați în primul rând de valoarea semnificației-dacă este mai mare de 0,05 (adică p > .05), variațiile noastre de grup pot fi tratate ca fiind egale. Cu toate acestea, dacă p < 0.05, avem diferențe inegale și am încălcat presupunerea omogenității varianțelor.,dacă testul Levene pentru egalitatea varianțelor este semnificativ din punct de vedere statistic, ceea ce indică faptul că variațiile de grup sunt inegale în populație, puteți corecta această încălcare prin faptul că nu utilizați estimarea cumulată pentru termenul de eroare pentru statistica t, ci folosind o ajustare a gradelor de libertate folosind metoda Welch-Satterthwaite., În realitate, probabil că nu veți fi auzit niciodată de aceste ajustări, deoarece statisticile SPSS ascund aceste informații și etichetează pur și simplu cele două opțiuni drept „diferențe egale asumate” și „diferențe egale neacceptate” fără a preciza în mod explicit testele de bază utilizate., Cu toate acestea, puteți vedea dovezi ale acestor teste ca mai jos:
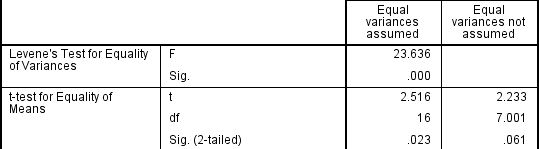
Din rezultatul de la Testul lui Levene pentru Egalitatea Varianțelor, putem respinge ipoteza nulă conform căreia nu există nicio diferență în diferențe între grupuri și a accepta ipoteza alternativă că există o diferență semnificativă statistic în diferențe între grupuri., Efectul de a nu putea presupune diferențe egale este evident în coloana finală a figurii de mai sus, unde vedem o reducere a valorii statisticii t și o reducere mare a gradelor de libertate (df). Aceasta are ca efect creșterea valorii p peste nivelul de semnificație critică de 0,05. În acest caz, prin urmare, nu acceptăm ipoteza alternativă și acceptăm că nu există diferențe semnificative statistic între mijloace. Aceasta nu ar fi fost concluzia noastră dacă nu am fi testat omogenitatea varianțelor.