ne gândim clasic la lumină ca întotdeauna călătorind în linii drepte, dar când undele luminoase trec pe lângă o barieră, ele tind să se îndoaie în jurul acelei bariere și să se răspândească. Difracția luminii apare atunci când un val de lumină trece printr-un colț sau printr-o deschidere sau o fantă care este fizic dimensiunea aproximativă a, sau chiar mai mică decât lungimea de undă a luminii.,

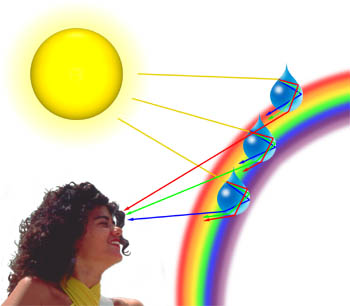
O demonstrație foarte simplă de difracție poate fi realizat prin mana ta în fața unei surse de lumină și apropie două degete în timp ce observarea luminii transmise între ele. Pe măsură ce degetele se apropie unul de celălalt și se apropie foarte mult, începeți să vedeți o serie de linii întunecate paralele cu degetele. Liniile paralele sunt de fapt modele de difracție. Acest fenomen poate apărea și atunci când lumina este „îndoită” în jurul particulelor care se află pe același ordin de mărime ca lungimea de undă a luminii., Un bun exemplu în acest sens este difracția luminii solare de către nori la care ne referim adesea ca o căptușeală de argint, ilustrată în Figura 1 cu un apus de soare frumos peste ocean.putem observa adesea nuanțe pastelate de albastru, roz, violet și verde în nori care sunt generate atunci când lumina este difractată de picăturile de apă din nori. Cantitatea de difracție depinde de lungimea de undă a luminii, lungimile de undă mai scurte fiind difractate la un unghi mai mare decât cele mai lungi (de fapt, lumina albastră și violetă sunt difractate la un unghi mai mare decât lumina roșie)., Ca un val de lumină călătoresc prin atmosfera întâlnește o picătură de apă, așa cum este ilustrat mai jos, este prima refractate la apa:interfață de aer, apoi se reflectă ca din nou întâlniri interfața. Fasciculul, care încă călătorește în interiorul picăturii de apă, este din nou refractat, deoarece lovește interfața pentru a treia oară. Această ultimă interacțiune cu interfața refractă lumina înapoi în atmosferă, dar, de asemenea, difractează o porțiune a luminii așa cum este ilustrat mai jos., Acest element de difracție conduce la un fenomen cunoscut sub numele de halo Cellini (cunoscut și sub numele de efectul Heiligenschein) în care un inel luminos de lumină înconjoară umbra capului observatorului.
termenii difracție și împrăștiere sunt adesea folosiți interschimbabil și sunt considerați a fi aproape sinonimi. Difracția descrie un caz specializat de împrăștiere a luminii în care un obiect cu caracteristici care se repetă în mod regulat (cum ar fi o grilă de difracție) produce o difracție ordonată a luminii într-un model de difracție., În lumea reală, majoritatea obiectelor au o formă foarte complexă și ar trebui considerate a fi compuse din multe caracteristici individuale de difracție care pot produce colectiv o împrăștiere aleatorie a luminii.unul dintre conceptele clasice și cele mai fundamentale care implică difracția este experimentul de difracție optică cu o singură fantă, realizat pentru prima dată la începutul secolului al XIX-lea. Atunci când un val de lumină se propagă printr-o fantă (sau deschidere) rezultatul depinde de dimensiunea fizică a diafragmei în raport cu lungimea de undă a fasciculului incident., Acest lucru este ilustrat în Figura 3 presupunând o coerente, monocromatice de undă emisă de sursă de punct S, similar cu lumina ca ar fi produs de un laser, trece prin diafragma d și este difractat, cu primar incident fascicul de lumină de aterizare de la punctul P și prima secundar maxima se produce la punctul Q.
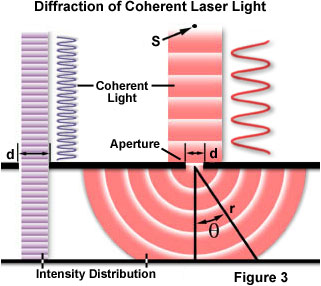
după Cum se arată în partea stângă a figurii, atunci când lungimea de undă (λ) este mult mai mică decât lățimea de deschidere (d), val pur și simplu călătorește mai departe în linie dreaptă, la fel cum ar face-o dacă ar fi fost o particulă sau nu de deschidere au fost prezenți., Cu toate acestea, atunci când lungimea de undă depășește dimensiunea deschiderii, am experienta de difracție a luminii, conform ecuației:
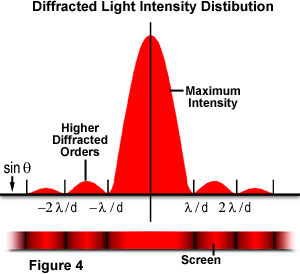
în cazul în Care θ este unghiul dintre incident central direcția de propagare și primul minim de difracție. Experimentul produce un maxim Central luminos, care este flancat pe ambele părți de maxime secundare, intensitatea fiecărui maxim secundar succesiv scăzând pe măsură ce distanța față de centru crește. Figura 4 ilustrează acest punct cu un grafic al intensității fasciculului față de raza de difracție., Rețineți că minimele care apar între maximele secundare sunt situate în multipli de π.
Acest experiment a fost explicat pentru prima dată de Augustin Fresnel care, împreună cu Thomas Young, a produs importante dovezi care să confirme că lumina călătorește în valuri. Din figurile de mai sus, vedem cum o lumină coerentă, monocromatică (în acest exemplu, iluminarea cu laser) emisă din punctul L este difractată de diafragma d., Fresnel a presupus că amplitudinea maximelor de ordinul întâi la punctul Q (definit ca eQ)ar fi dată de ecuația:
unde A este amplitudinea undei incidente, r este distanța dintre D și Q, iar f(χ) este o funcție a χ, un factor de înclinare introdus de Fresnel.
difracția luminii
explorați modul în care un fascicul de lumină este difractat atunci când trece printr-o fantă sau o deschidere îngustă. Reglați lungimea de undă și dimensiunea diafragmei și observați cum afectează acest lucru modelul de intensitate a difracției.,difracția luminii joacă un rol primordial în limitarea puterii de rezolvare a oricărui instrument optic (de exemplu: camere, Binocluri, Telescoape, microscoape și ochi). Puterea de rezolvare este capacitatea instrumentului optic de a produce imagini separate ale două puncte adiacente. Acest lucru este adesea determinat de calitatea lentilelor și oglinzilor din instrument, precum și de proprietățile mediului înconjurător (de obicei aerul). Natura undelor de lumină forțează o limită finală a puterii de rezoluție a tuturor instrumentelor optice.,discuțiile noastre despre difracție au folosit o fantă ca deschidere prin care lumina este difractată. Cu toate acestea, toate instrumentele optice au deschideri circulare, de exemplu pupila unui ochi sau diafragma circulară și lentilele unui microscop. Deschiderile circulare produc modele de difracție similare cu cele descrise mai sus, cu excepția faptului că modelul prezintă în mod natural o simetrie circulară. Analiza matematică a modelelor de difracție produse de o deschidere circulară este descrisă de ecuația:
unde θ (1) este poziția unghiulară a minimelor de difracție de ordinul întâi (primul inel întunecat), λ este lungimea de undă a luminii incidente, d este diametrul diafragmei și 1, 22 este o constantă. În majoritatea circumstanțelor, unghiul θ (1) este foarte mic, astfel încât aproximarea că sin și tan ale unghiului sunt randamente aproape egale:
Din aceste ecuații devine evident că maximul central este direct proporțional cu λ/d, făcând acest Maxim mai răspândit pentru lungimi de undă mai lungi și pentru deschideri mai mici., Mimina secundară a difracției a stabilit o limită la mărirea utilă a lentilelor obiective în microscopia optică, datorită difracției inerente a luminii de către aceste lentile. Oricât de perfectă ar fi obiectivul, imaginea unei surse punctuale de lumină produsă de obiectiv este însoțită de maxime secundare și superioare. Acest lucru ar putea fi eliminat numai dacă obiectivul ar avea un diametru infinit. Două obiecte separate de o distanță mai mică decât θ(1) nu pot fi rezolvate, indiferent cât de mare este puterea de mărire., În timp ce aceste ecuații au fost derivate pentru imaginea unei surse punctuale de lumină la o distanță infinită de deschidere, este o aproximare rezonabilă a puterii de rezoluție a unui microscop atunci când d este înlocuit cu diametrul lentilei obiectivului.astfel, dacă două obiecte se află la o distanță D una de cealaltă și se află la o distanță L de un observator, unghiul (exprimat în radiani) între ele este:
ceea ce ne face să putem condensa ultimele două ecuații pentru a produce:
unde D (0) este distanța minimă de separare dintre obiectele care le vor permite să fie rezolvate. Folosind această ecuație, ochiul uman poate rezolva obiecte separate de o distanță de 0,056 milimetri, cu toate acestea fotoreceptorii din retină nu sunt suficient de apropiați pentru a permite acest grad de rezoluție, iar 0,1 milimetri este un număr mai realist în condiții normale.puterea de rezolvare a microscoapelor optice este determinată de o serie de factori, inclusiv cei discutați, dar în cele mai ideale circumstanțe, acest număr este de aproximativ 0,2 micrometri., Acest număr trebuie să ia în considerare alinierea optică a microscopului, calitatea lentilelor, precum și lungimile de undă predominante ale luminii utilizate pentru imaginea specimenului. Deși de multe ori nu este necesar să se calculeze puterea de rezolvare exactă a fiecărui obiectiv (și ar fi o pierdere de timp în cele mai multe cazuri), este important să se înțeleagă capacitățile de lentile de microscop, deoarece acestea se aplică în lumea reală.
autori Contributivi
Mortimer Abramowitz-Olympus America, Inc., Două Unități De Centru Corporativ., Melville, New York, 11747.
Michael W., Davidson – National High Magnetic Field Laboratory, 1800 Est Paul Dirac Dr., Universitatea De Stat Din Florida, Tallahassee, Florida, 32310.