Introducere

regresia liniară, cunoscută și sub denumirea de regresie liniară simplă sau regresie liniară bivariată, este utilizată atunci când dorim să prezicem valoarea unei variabile dependente bazată pe valoarea unei variabile independente. De exemplu, puteți utiliza regresia liniară pentru a înțelege dacă performanța examenului poate fi prezisă pe baza timpului de revizuire (adică.,, variabila dvs. dependentă ar fi „performanța examenului”, măsurată de la 0-100 de mărci, iar variabila dvs. independentă ar fi” timpul de revizuire”, măsurat în ore). Alternativ, ai putea folosi de regresie liniară pentru a înțelege dacă consumul de țigări poate fi prezis pe baza de fumat durata (de exemplu, variabila dependentă ar fi „consumul de țigări”, măsurată în funcție de numărul de țigări consumate zilnic, iar variabila independentă ar fi „fumatul durata”, măsurată în zile). Dacă aveți două sau mai multe variabile independente, mai degrabă decât una, trebuie să utilizați regresie multiplă., Alternativ, dacă doriți doar să stabiliți dacă există o relație liniară, puteți utiliza corelația lui Pearson.

Nota: variabila dependentă este, de asemenea, menționată ca rezultat, obiectiv sau criteriu variabilă, în timp ce variabila independentă este, de asemenea, menționată ca predictor, explicative sau frecvență variabilă. În cele din urmă, indiferent de termenul pe care îl utilizați, cel mai bine este să fiți consecvent. Ne vom referi la acestea ca variabile dependente și independente în acest ghid.,în acest ghid, vă arătăm cum să efectuați regresia liniară folosind Stata, precum și să interpretați și să raportați rezultatele acestui test. Cu toate acestea, înainte de a vă prezenta această procedură, trebuie să înțelegeți diferitele ipoteze pe care datele dvs. trebuie să le îndeplinească pentru ca regresia liniară să vă ofere un rezultat valid. Vom discuta aceste ipoteze în continuare.

stata

ipoteze

există șapte „ipoteze” care stau la baza regresiei liniare. Dacă oricare dintre aceste șapte ipoteze nu sunt îndeplinite, nu puteți analiza datele dvs. folosind liniar, deoarece nu veți obține un rezultat valid., Deoarece ipotezele # 1 și #2 se referă la alegerea variabilelor dvs., acestea nu pot fi testate pentru utilizarea Stata. Cu toate acestea, ar trebui să decideți dacă studiul dvs. îndeplinește aceste ipoteze înainte de a trece mai departe.

  • ipoteza # 1: variabila dvs. dependentă trebuie măsurată la nivel continuu., Exemple de astfel de variabile continue includ înălțimea (măsurată în metri și centimetri), temperatura (măsurată în oC), salariu (măsurată în dolari SUA), revizia de timp (măsurat în ore), inteligență (măsurată utilizând scorul IQ), timpul de reacție (măsurat în milisecunde), testul de performanță (măsurată de la 0 la 100), vânzări (măsurată în numărul de tranzacții pe lună), și așa mai departe. Dacă nu sunteți sigur dacă variabila dvs. dependentă este continuă (adică măsurată la nivel de interval sau raport), consultați ghidul nostru tipuri de variabile.,
  • ipoteza #2: variabila dvs. independentă trebuie măsurată la nivel continuu sau categoric. Cu toate acestea, dacă aveți o variabilă independentă categorică, este mai frecvent să utilizați un test t independent (pentru 2 grupuri) sau ANOVA unidirecțional (pentru 3 grupuri sau mai multe). În cazul în care nu sunteți sigur, Exemple de variabile categorice includ sex (de exemplu, 2 grupe: masculin și feminin), etnie (de exemplu, 3 grupe: caucazian, afro-American și Hispanic), nivelul de activitate fizică (de exemplu, 4 grupe: sedentar, scăzut, moderat și înalt), și profesie (de exemplu,,, 5 grupuri: chirurg, medic, asistent medical, dentist, terapeut). În acest ghid, vă arătăm procedura de regresie liniară și ieșirea Stata atunci când atât variabilele dvs. dependente, cât și cele independente au fost măsurate la un nivel continuu.din fericire, puteți verifica ipotezele #3, #4, #5, #6 și # 7 folosind Stata. Când treceți la ipoteze #3, #4, #5, #6 și # 7, vă sugerăm să le testați în această ordine, deoarece reprezintă o ordine în care, dacă o încălcare a presupunerii nu este corectabilă, nu veți mai putea utiliza regresia liniară., De fapt, nu vă surprindeți dacă datele dvs. nu reușesc una sau mai multe dintre aceste ipoteze, deoarece acest lucru este destul de tipic atunci când lucrați cu date din lumea reală, mai degrabă decât Exemple de manuale, care adesea vă arată doar cum să efectuați regresia liniară atunci când totul merge bine. Cu toate acestea, nu vă faceți griji, deoarece chiar și atunci când datele dvs. nu reușesc anumite ipoteze, există adesea o soluție pentru a depăși acest lucru (de exemplu, transformarea datelor dvs. sau utilizarea unui alt test statistic)., Amintiți-vă că, dacă nu verificați dacă datele îndeplinesc aceste ipoteze sau le testați incorect, rezultatele pe care le obțineți atunci când executați regresia liniară ar putea să nu fie valide.

    • ipoteza #3: trebuie să existe o relație liniară între variabilele dependente și cele independente. În timp ce există o serie de moduri de a verifica dacă există o relație liniară între cele două variabile, vă sugerăm să creați un scatterplot folosind Stata, unde puteți plota variabila dependentă împotriva variabilei dvs. independente., Apoi puteți inspecta vizual scatterplot pentru a verifica liniaritatea. Ta scatterplot poate arata ceva de genul una dintre următoarele:

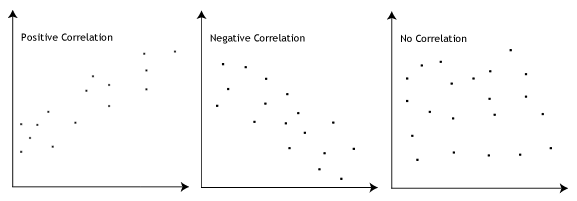
      Dacă relația afișate în scatterplot nu este liniară, va trebui să fie executați un non-analiza de regresie liniară sau „transforma” datele, pe care le puteți face folosind Stata.

    • ipoteza #4: nu ar trebui să existe valori superioare semnificative. Valorile aberante sunt pur și simplu puncte de date unice din datele dvs. care nu respectă modelul obișnuit (de ex.,, într-un studiu al scorurilor IQ ale elevilor 100, unde Scorul mediu a fost de 108, cu doar o mică variație între studenți, un student a avut un scor de 156, ceea ce este foarte neobișnuit și poate chiar să o plaseze în top 1% din scorurile IQ la nivel global). Următoarele scatterplots evidenția impactul potențial al aberante:

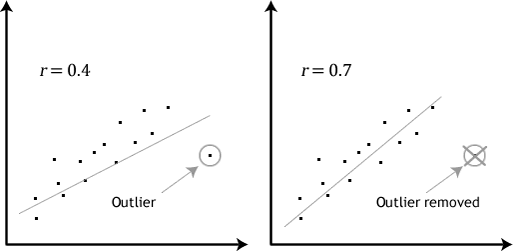
      problema cu valori extreme este că acestea pot avea un efect negativ asupra ecuația de regresie, care este folosit pentru a prezice valoarea variabilei dependente pe baza variabilei independente., Acest lucru va schimba rezultatul pe care Stata îl produce și va reduce precizia predictivă a rezultatelor. Din fericire, puteți utiliza Stata pentru a efectua diagnosticarea casewise pentru a vă ajuta să detectați posibilele valori.

    • ipoteza # 5: ar trebui să aveți independența observațiilor, pe care o puteți verifica cu ușurință folosind statistica Durbin-Watson, care este un test simplu de rulat folosind Stata.
    • ipoteza # 6: datele dvs. trebuie să arate homoscedasticitate, care este locul în care variațiile de-a lungul liniei de cea mai bună potrivire rămân similare pe măsură ce vă deplasați de-a lungul liniei., Cele două scatterplots de mai jos oferă exemple simple de date care îndeplinește această ipoteză și una care nu reușește ipoteza:

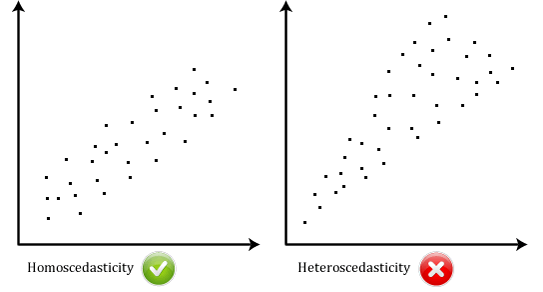
      atunci Când vă analizați propriile date, va fi norocos dacă scatterplot se pare ca oricare dintre cele doua de mai sus. În timp ce acestea ajută la ilustrarea diferențelor de date care îndeplinesc sau încalcă ipoteza homoscedasticității, datele din lumea reală sunt adesea mult mai dezordonate., Puteți verifica dacă datele dvs. au arătat homoscedasticitate prin trasarea reziduurilor standardizate de regresie în raport cu valoarea prezisă standardizată de regresie.

    • ipoteza # 7: în cele din urmă, trebuie să verificați dacă reziduurile (Erorile) liniei de regresie sunt distribuite aproximativ în mod normal. Două metode comune pentru a verifica această ipoteză includ utilizarea fie a unei histograme (cu o curbă normală suprapusă), fie a unui complot P-P Normal.

    în practică, verificarea ipotezelor #3, #4, #5, #6 și # 7 va dura probabil cea mai mare parte a timpului dvs. atunci când efectuați regresia liniară., Cu toate acestea, nu este o sarcină dificilă, iar Stata oferă toate instrumentele de care aveți nevoie pentru a face acest lucru.

    în secțiunea procedură, ilustrăm procedura Stata necesară pentru a efectua regresia liniară presupunând că nu au fost încălcate ipoteze. În primul rând, am prezentat exemplul pe care îl folosim pentru a explica procedura de regresie liniară în Stata.studiile arată că exercițiile fizice pot ajuta la prevenirea bolilor de inimă. În limite rezonabile, cu cât exersați mai mult, cu atât aveți mai puțin riscul de a suferi de boli de inimă., O modalitate prin care exercițiile fizice vă reduc riscul de a suferi de boli de inimă este prin reducerea unei grăsimi din sânge, numită colesterol. Cu cât exersați mai mult, cu atât concentrația de colesterol este mai mică. Mai mult, s – a demonstrat recent că timpul pe care îl petreci uitându – te la televizor-un indicator al unui stil de viață sedentar-ar putea fi un bun predictor al bolilor de inimă (adică, cu cât te uiți mai mult la televizor, cu atât riscul de boli de inimă este mai mare).,prin urmare, un cercetător a decis să determine dacă concentrația de colesterol a fost legată de timpul petrecut vizionând televizorul la bărbații sănătoși de 45 până la 65 de ani (o categorie de persoane cu risc). De exemplu, pe măsură ce oamenii petrec mai mult timp uitându-se la televizor, concentrația lor de colesterol a crescut și ea (o relație pozitivă); sau sa întâmplat contrariul? Cercetătorul a dorit, de asemenea, să cunoască proporția concentrației de colesterol pe care timpul petrecut la televizor ar putea explica, precum și posibilitatea de a prezice concentrația de colesterol., Cercetătorul ar putea apoi să stabilească dacă, de exemplu, persoanele care au petrecut opt ore petrecute la televizor pe zi au avut un nivel periculos de ridicat al concentrației de colesterol în comparație cu persoanele care urmăresc doar două ore de televizor.pentru a efectua analiza, cercetătorul a recrutat 100 de participanți sănătoși de sex masculin cu vârste cuprinse între 45 și 65 de ani. Cantitatea de timp petrecută la vizionarea TV (adică variabila independentă, time_tv) și concentrația de colesterol (adică variabila dependentă, colesterolul) au fost înregistrate pentru toți cei 100 de participanți., Exprimat în termeni variabili, cercetătorul a dorit să regreseze colesterolul la time_tv.

    notă: exemplul și datele utilizate pentru acest ghid sunt fictive. Tocmai le-am creat în scopul acestui ghid.

    Stata

    configurare în Stata

    Notă: Nu contează dacă creați mai întâi variabila dependentă sau independentă.

    după crearea acestor două variabile-time_tv și colesterol – am introdus scorurile pentru fiecare în cele două coloane ale foii de calcul editor de date (Editare) (adică.,, timpul în ore, în care participanții au vizionat TV în coloana din stânga (de exemplu, time_tv, variabila independentă), și a participanților concentrația colesterolului în mmol/L în coloana din dreapta (de exemplu, colesterol, variabila dependentă), așa cum se arată mai jos:

    Publicat cu permisiunea scrisă de la StataCorp LP.,

    Stata

    procedura de testare în Stata

    În această secțiune, vă arătăm cum să analizați datele utilizând regresia liniară în Stata atunci când cele șase ipoteze din secțiunea anterioară, ipoteze, nu au fost încălcate. Puteți efectua regresie liniară folosind codul sau interfața grafică de utilizator (GUI) a Stata. După ce ați efectuat analiza, vă arătăm cum să interpretați rezultatele. Mai întâi, alegeți dacă doriți să utilizați codul sau interfața grafică de utilizator (GUI) a Stata.,

    Cod

    codul pentru a efectua liniar de regresie pe date are forma:

    regres DependentVariable IndependentVariable

    Acest cod este introdus în caseta de mai jos:

    Publicat cu permisiunea scrisă de la StataCorp LP.,

    Folosind exemplul nostru, în cazul în care variabila dependentă este colesterolul, iar variabila independentă este time_tv, necesar codul va fi:

    regres colesterol time_tv

    Notă 1: trebuie să fie precise atunci când introduceți codul în cutie. Codul este „sensibil la majuscule”. De exemplu, dacă ați introdus „colesterol” în cazul în care ” C ” este majuscule, mai degrabă decât litere mici (adică.,, un mic „c”), care ar trebui să fie, veți primi un mesaj de eroare, cum ar fi următoarele:

    Nota 2: Dacă sunteți încă obtinerea mesaj de eroare în Nota 2: mai sus, este în valoare de verificat numele dat două variabile în data Editor atunci când configurați un fișier (de exemplu, vezi Datele Editor de ecran de mai sus)., În caseta de pe partea dreaptă de Date Editor ecran, acesta este modul în care ai scris variabile în secțiune, nu secțiunea de care aveți nevoie pentru a intra în cod (a se vedea mai jos pentru variabila dependentă). Acest lucru poate părea evident, dar este o eroare care se face uneori, rezultând eroarea din nota 2 de mai sus.

    prin Urmare, introduceți codul de regres colesterol time_tv, și apăsați „Return/Enter” buton de pe tastatură.,

    Publicat cu permisiunea scrisă de la StataCorp LP.

    puteți vedea ieșirea Stata care va fi produsă aici.,

    Interfață Grafică de Utilizator (GUI)

    Cele trei etape necesare pentru a efectua de regresie liniară în Stata 12 și 13 sunt prezentate mai jos:

    1. faceți Clic pe Statistici > modele Liniare și legate > regresie Liniară în meniul principal, așa cum se arată mai jos:

      Publicat cu permisiunea scrisă de la StataCorp LP.,

      va fi prezentat cu Regres – regresie Liniară casetă de dialog:

      Publicat cu permisiunea scrisă de la StataCorp LP.

    2. selectați colesterolul din variabila dependentă: caseta derulantă și time_tv din variabilele independente: caseta derulantă. Va termina cu următorul ecran:

      Publicat cu permisiunea scrisă de la StataCorp LP.,

    3. faceți Clic pe buton. Aceasta va genera ieșirea.

    Stata

    Ieșire de analiza de regresie liniară în Stata

    în Cazul în care datele transmise ipoteza #3 (de exemplu, există o relație liniară între două variabile), #4 (de exemplu, nu au existat excepții semnificative), adormirea maicii domnului #5 (de exemplu, ai avut independenței de observații), adormirea maicii domnului #6 (de exemplu, datele au aratat homoscedasticității) și presupunerea #7 (de exemplu,,, abaterilor (erorilor) a fost de aproximativ normal distribuite), pe care am explicat mai devreme în secțiunea Ipoteze, va trebui doar să se interpreteze următoarele regresie liniară ieșire în Stata:

    Publicat cu permisiunea scrisă de la StataCorp LP.,

    ieșirea constă din patru informații importante: (a) valoarea R2 (rândul”R-pătrat”) reprezintă proporția de varianță în variabila dependentă care poate fi explicată de variabila noastră independentă (tehnic este proporția de variație contabilizată de modelul de regresie deasupra și dincolo de modelul mediu). Cu toate acestea, R2 se bazează pe eșantion și este o estimare părtinitoare pozitivă a proporției varianței variabilei dependente contabilizate de modelul de regresie (adică.,, este prea mare); (b) o R2 ajustat valoarea („Adj R-squared” rând), care corectează prejudecată pozitivă de a oferi o valoare care ar fi de așteptat în rândul populației; (c) valoarea F grade de libertate („F( 1, 98)”) și semnificația statistică a modelului de regresie („Prob > F” row); și (d) coeficienții pentru constantă și variabilă independentă („Coef.”coloana), care este informația de care aveți nevoie pentru a prezice variabila dependentă, colesterolul, folosind variabila independentă, time_tv.

    în acest exemplu, R2 = 0.151. Ajustat R2 = 0,143 (la 3 d. P.,), ceea ce înseamnă că variabila independentă, time_tv, explică 14,3% din variabilitatea variabilei dependente, colesterolul, în populație. R2 ajustat este, de asemenea, o estimare a mărimii efectului, care la 0.143 (14.3%), indică o mărime medie a efectului, conform clasificării lui Cohen (1988). Cu toate acestea, în mod normal, R2 nu este ajustat R2 care este raportat în rezultate. În acest exemplu, modelul de regresie este semnificativ statistic, F(1, 98) = 17.47, p = .0001., Acest lucru indică faptul că, în general, modelul aplicat poate prezice semnificativ statistic variabila dependentă, colesterolul.

    notă: prezentăm rezultatul din analiza de regresie liniară de mai sus. Cu toate acestea, deoarece ar fi trebuit să vă testați datele pentru ipotezele pe care le-am explicat mai devreme în secțiunea ipoteze, va trebui, de asemenea, să interpretați rezultatul Stata care a fost produs atunci când ați testat aceste ipoteze. Aceasta include: (a) scatterplots ați folosit pentru a verifica dacă a existat o relație liniară între cele două variabile (adică.,,, Adormirea maicii domnului #3); (b) casewise de diagnosticare pentru a verifica nu au existat excepții semnificative (de exemplu, Ipoteza nr. 4); (c) ieșirea din statistica Durbin-Watson pentru a verifica pentru independența de observații (de exemplu, Ipoteza #5); (d) un scatterplot de regresie reziduurilor standardizate împotriva regresie standardizat prezis valoare pentru a determina dacă datele au aratat omoscedasticitate (de exemplu, Ipoteza #6); și o histogramă (cu suprapune curba normală) si Normal P-P Plot pentru a verifica dacă valorile reziduale (erorile) a fost de aproximativ normal distribuite (de exemplu, Ipoteza #7)., De asemenea, rețineți că, dacă datele dvs. nu au reușit oricare dintre aceste ipoteze, rezultatul pe care îl obțineți din procedura de regresie liniară (adică rezultatul pe care îl discutăm mai sus) nu va mai fi relevant și este posibil să fiți nevoit să efectuați un test statistic diferit pentru a vă analiza datele.,

    Stata

    Raportare la ieșire din analiza de regresie liniară

    atunci Când raportul de ieșire linear de regresie, este o bună practică să includă: (a) o introducere în analiza pe care le efectuează; (b) informații despre probă, inclusiv orice valori lipsă; (c) se observă valoarea F, grade de libertate și nivelul de semnificație (de exemplu, p-value); (d) procentul din varianța variabilei dependente explicată de variabila independentă (de exemplu, R2 Ajustat ); și (e) ecuația de regresie pentru modelul dumneavoastră., Pe baza rezultatelor de mai sus, am putea raporta rezultatele acestui studiu după cum urmează:

    • General

    o regresie liniară a stabilit că timpul zilnic petrecut la televizor ar putea prezice semnificativ statistic concentrația de colesterol, F(1, 98) = 17, 47, p = .0001 și timpul petrecut la televizor au reprezentat 14,3% din variabilitatea explicată a concentrației de colesterol. Ecuația de regresie a fost: concentrația estimată a colesterolului = -2.135 + 0.044 x (timpul petrecut la televizor).,

    în plus față de raportarea rezultatelor ca mai sus, o diagramă poate fi utilizată pentru a prezenta vizual rezultatele. De exemplu, puteți face acest lucru folosind un scatterplot cu intervale de încredere și predicție (deși nu este foarte comun să adăugați ultimul). Acest lucru poate face mai ușor pentru alții să înțeleagă rezultatele. Mai mult, puteți utiliza ecuația de regresie liniară pentru a face predicții despre valoarea variabilei dependente pe baza diferitelor valori ale variabilei independente., În timp ce Stata nu produce aceste valori ca parte a procedurii de regresie liniară de mai sus, există o procedură în Stata pe care o puteți utiliza pentru a face acest lucru.