|
|
die Varianz misst, wie weit ein Satz an Daten, verteilt wird. Eine Varianz von Null gibt an, dass alle Datenwerte identisch sind. Alle Nicht-Null-Varianzen sind positiv.
|
Eine kleine Varianz zeigt an, dass die Datenpunkte sehr nahe am Mittelwert und zueinander liegen., Eine hohe Varianz zeigt an, dass die Datenpunkte sehr weit vom Mittelwert und voneinander entfernt sind. Varianz ist der Durchschnitt der quadratischen Abstände von jedem Punkt zum Mittelwert.
Der einzige Unterschied ist das quadrieren der Entfernungen.
Prozess: (1) Finden Sie den Mittelwert (Durchschnitt) der Menge. (2) Subtrahieren Sie jeden Datenwert vom Mittelwert, um seinen Abstand vom Mittelwert zu ermitteln. (3) Quadrat alle Entfernungen. (4) Fügen Sie alle Quadrate der Entfernungen., (4) Dividieren Sie durch die Anzahl der Daten (für Populationsvarianz).
Ein Problem mit der Varianz ist, dass sie nicht die gleiche Maßeinheit wie die ursprünglichen Daten hat. Beispielsweise weisen Originaldaten, die Längen enthalten, die in Fuß gemessen werden, eine Varianz auf, die in Quadratfuß gemessen wird.,
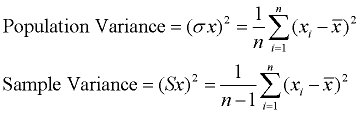 |
 |
|
![]()
|
|
Standardabweichung zeigt an, wie viel Variation (Streuung, Streuung, Streuung) vom Mittelwert vorhanden ist., Es stellt eine typische Abweichung vom Mittelwert. Es ist ein beliebtes Maß für die Variabilität, da es zu den ursprünglichen Maßeinheiten des Datensatzes zurückkehrt.
|
Eine niedrige Standardabweichung zeigt an, dass die Datenpunkte sehr nahe am Mittelwert liegen. Eine hohe Standardabweichung zeigt an, dass die Datenpunkte über einen großen Wertebereich verteilt sind.
Die Standardabweichung kann als eine „Standard“ Art und Weise zu wissen, was normal ist (typisch), was sehr groß ist, und was in dem Datensatz sehr klein.,
Die Standardabweichung ist ein beliebtes Maß für die Variabilität, da sie zu den ursprünglichen Maßeinheiten des Datensatzes zurückkehrt. Zum Beispiel haben Originaldaten, die Längen enthalten, die in Fuß gemessen werden, eine Standardabweichung, die auch in Fuß gemessen wird.,
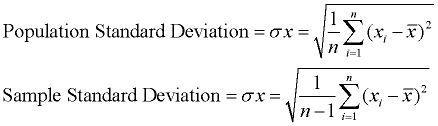 |
 |
|
Die Standardabweichung ist einfach die Quadratwurzel der Varianz. Diese Beschreibung ist für die Berechnung der Bevölkerung Standardabweichung. Wenn eine Standardabweichung erforderlich ist, dividieren Sie durch n – 1 anstelle von n., Da die Standardabweichung die Quadratwurzel der Varianz ist, müssen wir zuerst die Varianz berechnen. |
|
|
1. Finde den Mittelwert.
|
|
|
2. Subtrahieren Sie den Mittelwert von jedem Datenwert und quadrieren Sie jede dieser Differenzen (die quadratischen Differenzen).
|
|
|
3. Ermitteln Sie den Durchschnitt der quadratischen Unterschiede (addieren Sie sie und dividieren Sie sie durch die Anzahl der Datenwerte). Dies wird die Varianz sein.,
|
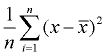 Varianz |
|
4. Nimm die Quadratwurzel. Dies wird die Populationsstandardabweichung sein. Runden Sie die Antwort gemäß den Anweisungen im Problem ab.
|
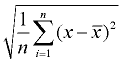 Standardabweichung |
![]()
![]() Normale Kurve
Normale Kurve
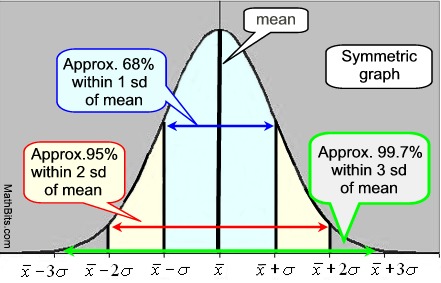
Eine normale Kurve ist eine symmetrische, glockenförmige Kurve., Der Mittelpunkt des Diagramms ist der Mittelwert und die Höhe und Breite des Diagramms werden durch die Standardabweichung bestimmt. Wenn die Standardabweichung klein ist, ist die Kurve hoch und schmal verteilt. Wenn die Standardabweichung groß ist, ist die Kurve kurz und breit verteilt. Der Mittelwert und der Median haben den gleichen Wert in einer normalen Kurve.
|
Normale Kurve Empirische Regel: * 68% der Daten liegen innerhalb einer Standardabweichung des Mittelwerts., * 95% der Daten liegen innerhalb von zwei Standardabweichungen des Mittelwerts. * 99,7% der Daten liegen innerhalb von drei Standardabweichungen des Mittelwerts. IQR für eine normale Kurve ist 1.34896 x Standardabweichung. |
 |
![]()
