Annahme der Normalität der abhängigen Variablen
Der unabhängige t-Test erfordert, dass die abhängige Variable ungefähr normal innerhalb jeder Gruppe verteilt ist.
Hinweis: Technisch gesehen müssen die Residuen normal verteilt werden, aber für einen unabhängigen T-Test erhalten Sie beide das gleiche Ergebnis.,
Sie können dies mit einer Reihe verschiedener Tests testen, aber der Shapiro-Wilks-Test der Normalität oder eine grafische Methode, wie z. B. ein Q-Q-Diagramm, sind sehr häufig. Sie können diese Tests mithilfe von SPSS-Statistiken ausführen, deren Verfahren Sie in unserem Handbuch zu Tests für Normalität finden. Der t-Test wird jedoch als robuster Test in Bezug auf die Annahme von Normalität beschrieben. Dies bedeutet, dass eine Abweichung von der Normalität keinen großen Einfluss auf die Fehlerraten vom Typ I hat. Die Ausnahme ist, wenn das Verhältnis der kleinsten zur größten Gruppengröße größer als 1 ist.,5 (größte im vergleich zu kleinste).
Was tun, wenn Sie gegen die Normalitätsannahme verstoßen
Wenn Sie feststellen, dass entweder eine oder beide Daten Ihrer Gruppe nicht annähernd normal verteilt sind und sich die Gruppengrößen stark unterscheiden, haben Sie zwei Möglichkeiten: (1) Transformieren Sie Ihre Daten so, dass die Daten normal verteilt werden (um dies in der SPSS-Statistik zu tun, lesen Sie unseren Leitfaden zum Transformieren von Daten) oder (2) Führen Sie den Mann-Whitney U-Test aus, bei dem es sich um einen nicht parametrischen Test handelt, der keine Normalitätsannahme erfordert (um der Mann-Whitney U Test).,
Annahme der Homogenität der Varianz
Der unabhängige t-Test geht davon aus, dass die Varianzen der beiden Gruppen, die Sie messen, in der Population gleich sind. Wenn Ihre Varianzen ungleich sind, kann dies die Fehlerrate vom Typ I beeinflussen. Die Annahme der Homogenität der Varianz kann mit dem Levene-Test der Varianzgleichheit getestet werden, der in der SPSS-Statistik beim Ausführen des unabhängigen t-Testverfahrens erstellt wird., Wenn Sie Levenes Test der Gleichheit von Varianzen in SPSS-Statistiken durchgeführt haben, erhalten Sie ein ähnliches Ergebnis wie unten:

Dieser Test auf Homogenität der Varianz liefert eine F-Statistik und einen Signifikanzwert (p-Wert). Wir beschäftigen uns hauptsächlich mit dem Signifikanzwert – wenn er größer als 0,05 ist (dh p > .05) können unsere Gruppenvarianzen als gleich behandelt werden. Wenn jedoch p 0.05, haben wir ungleiche Varianzen und wir haben die Annahme der Homogenität von Varianzen verletzt.,
Überwindung einer Verletzung der Annahme der Homogenität der Varianz
Wenn der Levene-Test auf Varianzgleichheit statistisch signifikant ist, was anzeigt, dass die Gruppenvarianzen in der Population ungleich sind, können Sie diese Verletzung korrigieren, indem Sie nicht die gepoolte Schätzung für den Fehlerterm für die t-Statistik verwenden, sondern eine Anpassung an die Freiheitsgrade mit der Welch-Satterthwaite-Methode., In der Realität werden Sie wahrscheinlich noch nie von diesen Anpassungen gehört haben, da SPSS Statistics diese Informationen verbirgt und die beiden Optionen einfach als „Gleiche angenommene Varianzen“ und „Gleiche nicht angenommene Varianzen“ bezeichnet, ohne die zugrunde liegenden verwendeten Tests explizit anzugeben., Sie können die Beweise für diese Tests jedoch wie folgt sehen:
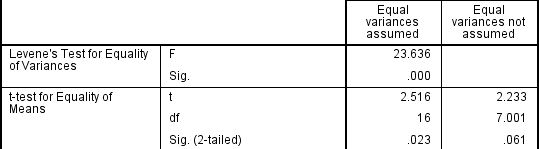
Aus dem Ergebnis von Levenes Test auf Varianzgleichheit können wir die Nullhypothese ablehnen, dass es keinen Unterschied in den Varianzen zwischen den Gruppen gibt, und die alternative Hypothese akzeptieren, dass es einen statistisch signifikanten Unterschied in den Varianzen zwischen den Gruppen gibt., Der Effekt, nicht gleiche Varianzen annehmen zu können, zeigt sich in der letzten Spalte der obigen Abbildung, in der der Wert der t-Statistik verringert und die Freiheitsgrade stark verringert werden (df). Dies hat den Effekt, dass der p-Wert über das kritische Signifikanzniveau von 0,05 erhöht wird. In diesem Fall akzeptieren wir daher die alternative Hypothese nicht und akzeptieren, dass es keine statistisch signifikanten Unterschiede zwischen den Mitteln gibt. Dies wäre nicht unsere Schlussfolgerung gewesen, wenn wir nicht auf Homogenität der Varianzen getestet hätten.