varians mäter hur långt en uppsättning data sprids ut. En varians på noll indikerar att alla datavärden är identiska. Alla icke-nollvarianser är positiva.

en liten varians indikerar att datapunkterna tenderar att vara mycket nära medelvärdet och varandra., En hög varians indikerar att datapunkterna är mycket utspridda från medelvärdet och från varandra. Varians är genomsnittet av de kvadrerade avstånden från varje punkt till medelvärdet.

processen att hitta variansen är mycket lik att hitta den galna, genomsnittliga absoluta avvikelsen.
den enda skillnaden är kvadrering av avstånden.
Process: (1) Hitta medelvärdet (genomsnitt) av uppsättningen. (2) subtrahera varje datavärde från medelvärdet för att hitta sitt avstånd från medelvärdet. (3) kvadrera alla avstånd. (4) Lägg till alla rutor av avstånden., (4) dividera med antalet bitar av data (för populationsvarians).

ett problem med variansen är att det inte har samma måttenhet som de ursprungliga uppgifterna. Till exempel har originaldata som innehåller längder uppmätta i fötter en varians mätt i kvadratfot.,

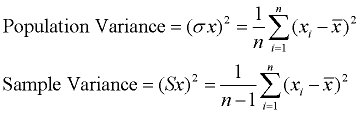Don’t ROUND too soon! When working with the formulas for variance and standard deviation, be careful to avoid rounding too soon., Vid beräkning för hand, alltid bära fler decimaler inom beräkningarna än vad som förväntas för slutresultatet. Om du arbetar med en räknare, bär det fulla värdet av kalkylatorposterna tills du kommer fram till slutresultatet.

standardavvikelse visar hur mycket variation (spridning, spridning, spridning) från medelvärdet finns., Det representerar en ”typisk” avvikelse från medelvärdet. Det är ett populärt mått på variabilitet eftersom det återgår till de ursprungliga måttenheterna för datauppsättningen.

en låg standardavvikelse indikerar att datapunkterna tenderar att vara mycket nära medelvärdet. En hög standardavvikelse indikerar att datapunkterna sprids ut över ett stort antal värden.
standardavvikelsen kan ses som ett ”standard” sätt att veta vad som är normalt( typiskt), vad som är mycket stort och vad som är mycket litet i datauppsättningen.,

standardavvikelse är ett populärt mått på variabilitet eftersom det återgår till de ursprungliga måttenheterna för datauppsättningen. Till exempel har originaldata som innehåller längder uppmätta i fötter en standardavvikelse som också mäts i fötter.,

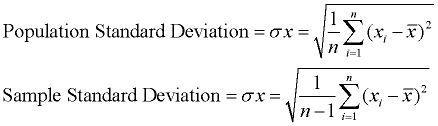för att beräkna standardavvikelsen för hand:
standardavvikelsen är helt enkelt kvadratroten av variansen.
denna beskrivning är avsedd för beräkning av populationsstandardavvikelse. Om prov standardavvikelse behövs, dividera med n-1 istället för n., Eftersom standardavvikelsen är kvadratroten av variansen måste vi först beräkna variansen.
1. Hitta medelvärdet.
2. Subtrahera medelvärdet från varje datavärde och kvadrera var och en av dessa skillnader (de kvadrerade skillnaderna).
3. Hitta genomsnittet av de kvadrerade skillnaderna (Lägg till dem och dela med räkningen av datavärdena). Detta kommer att vara variansen.,

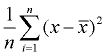varians
4. Ta kvadratroten. Detta kommer att vara befolkningens standardavvikelse. Runda svaret enligt anvisningarna i problemet.

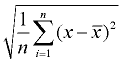standardavvikelse

Normal kurva

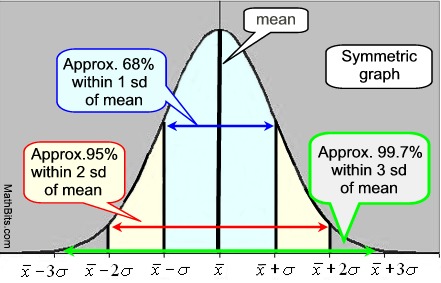
en normal kurva är en symmetrisk, klockformad kurva., Grafens centrum är medelvärdet, och grafens höjd och bredd bestäms av standardavvikelsen. När standardavvikelsen är liten kommer kurvan att vara lång och smal i spridning. När standardavvikelsen är stor kommer kurvan att vara kort och bred i spridning. Medelvärdet och medianvärdet har samma värde i en normal kurva.

Normal Curve empirisk regel:
ungefärligt …

• 68% av uppgifterna ligger inom en standardavvikelse för medelvärdet.,

• 95% av data ligger inom två standardavvikelser av medelvärdet.

• 99,7% av data ligger inom tre standardavvikelser av medelvärdet.

IQR för en normal kurva är 1.34896 X standardavvikelse.