Support Vector Machine eller SVM är en av de mest populära övervakade inlärningsalgoritmer, som används för klassificering samt Regressionsproblem. Men i första hand används den för klassificeringsproblem i maskininlärning.
målet med SVM-algoritmen är att skapa den bästa linjen eller beslutsgränsen som kan segregera n-dimensionellt utrymme i klasser så att vi enkelt kan sätta den nya datapunkten i rätt kategori i framtiden., Denna bästa beslutsgräns kallas en hyperplan.
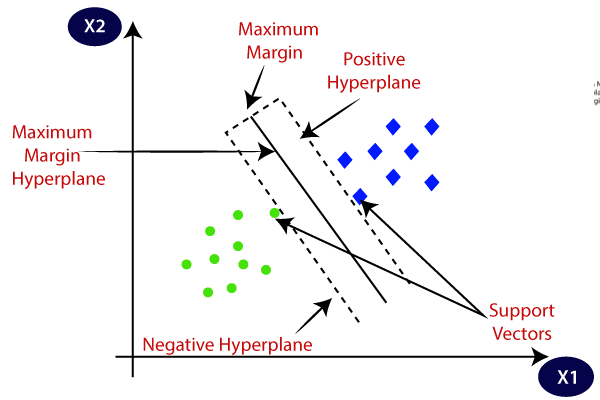
SVM väljer de extrema punkter / vektorer som hjälper till att skapa hyperplanet. Dessa extrema fall kallas som stödvektorer, och därmed kallas algoritmen som stödvektormaskin. Tänk på nedanstående diagram där det finns två olika kategorier som klassificeras med hjälp av en beslutsgräns eller hyperplan:
exempel: SVM kan förstås med det exempel som vi har använt i KNN-klassificeraren., Antag att vi ser en konstig katt som också har vissa funktioner hos hundar, så om vi vill ha en modell som exakt kan identifiera om det är en katt eller hund, så kan en sådan modell skapas med hjälp av SVM-algoritmen. Vi kommer först att träna vår modell med massor av bilder av katter och hundar så att den kan lära sig om olika funktioner hos katter och hundar, och sedan testar vi det med denna konstiga varelse. Så som stödvektor skapar en beslutsgräns mellan dessa två data (katt och hund) och väljer extrema fall (stödvektorer), kommer det att se det extrema fallet med katt och hund., På grundval av stödvektorerna kommer det att klassificera det som en katt. Tänk på följande diagram:
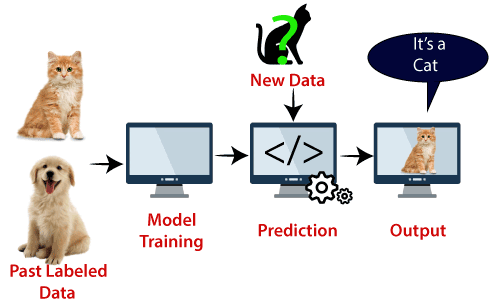
SVM-algoritmen kan användas för ansiktsigenkänning, bildklassificering, textkategorisering etc.
typer av SVM
SVM kan vara av två typer:
- linjär SVM: linjär SVM används för linjärt separerbar data, vilket innebär att om en dataset kan klassificeras i två klasser genom att använda en enda rak linje, kallas sådana data som linjärt separerbar data och klassificeraren används som linjär SVM-klassificerare.,
- icke-linjär SVM: icke-linjär SVM används för icke-linjärt separerade data, vilket innebär att om en datauppsättning inte kan klassificeras med hjälp av en rak linje, kallas sådana data som icke-linjär data och klassificerare som används kallas som icke-linjär SVM-klassificerare.
hyperplan och Stödvektorer i SVM-algoritmen:
hyperplan: det kan finnas flera linjer / beslutsgränser för att segregera klasserna i n-dimensionellt utrymme, men vi måste ta reda på den bästa beslutsgränsen som hjälper till att klassificera datapunkterna. Denna bästa gräns är känd som SVM: s hyperplan.,
hyperplanets dimensioner beror på funktionerna som finns i datauppsättningen, vilket innebär att om det finns 2 funktioner (som visas i bilden), kommer hyperplane att vara en rak linje. Och om det finns 3 funktioner, kommer hyperplane att vara ett 2-dimensionsplan.
Vi skapar alltid ett hyperplan som har en maximal marginal, vilket innebär det maximala avståndet mellan datapunkterna.
Supportvektorer:
de datapunkter eller vektorer som ligger närmast hyperplanet och som påverkar hyperplanets position kallas som Stödvektor., Eftersom dessa vektorer stöder hyperplanet kallas de därför en Stödvektor.
hur fungerar SVM?
linjär SVM:
arbetet med SVM-algoritmen kan förstås med hjälp av ett exempel. Antag att vi har en datauppsättning som har två taggar (grön och blå), och datauppsättningen har två funktioner x1 och x2. Vi vill ha en klassificerare som kan klassificera paret(x1, x2) av koordinater i antingen grönt eller blått. Tänk på bilden nedan:
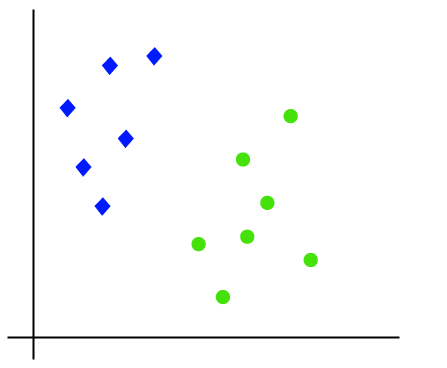
eftersom det är 2-D utrymme så genom att bara använda en rak linje, kan vi enkelt separera dessa två klasser., Men det kan finnas flera linjer som kan skilja dessa klasser. Tänk på bilden nedan:
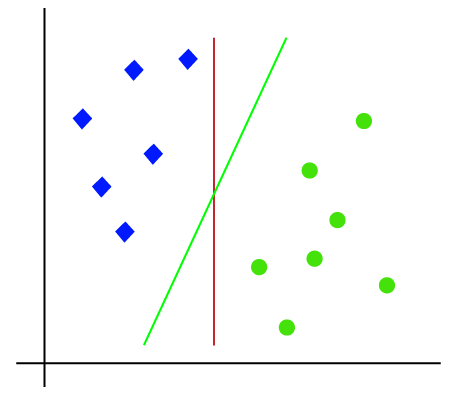
SVM-algoritmen hjälper därför till att hitta den bästa linjen eller beslutsgränsen; den här bästa gränsen eller regionen kallas som hyperplan. SVM-algoritmen hittar den närmaste punkten av linjerna från båda klasserna. Dessa punkter kallas stödvektorer. Avståndet mellan vektorerna och hyperplanet kallas som marginal. Och målet med SVM är att maximera denna marginal. Hyperplanet med maximal marginal kallas den optimala hyperplanet.,
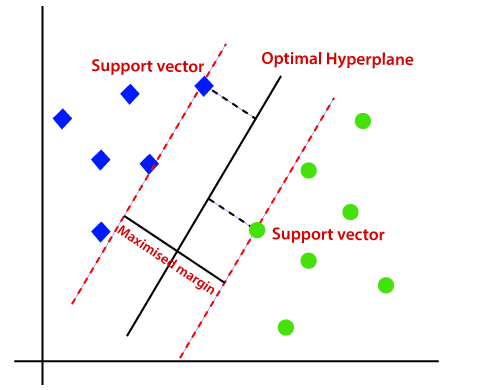
Icke-linjär SVM:
om data är linjärt ordnade kan vi separera det med en rak linje, men för icke-linjära data kan vi inte rita en enda rak linje. Tänk på bilden nedan:
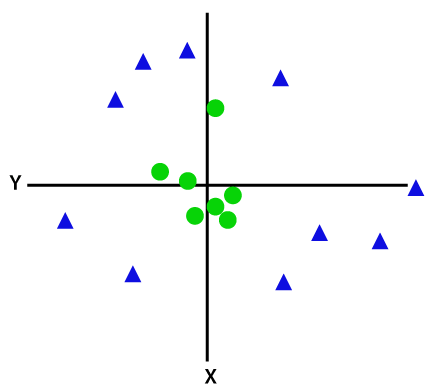
för att separera dessa datapunkter måste vi lägga till ytterligare en dimension. För linjära data har vi använt två dimensioner x och y, så för icke-linjära data lägger vi till en tredje dimension z., Det kan beräknas som:
z=x2 +y2
genom att lägga till den tredje dimensionen blir provutrymmet som nedan bild:
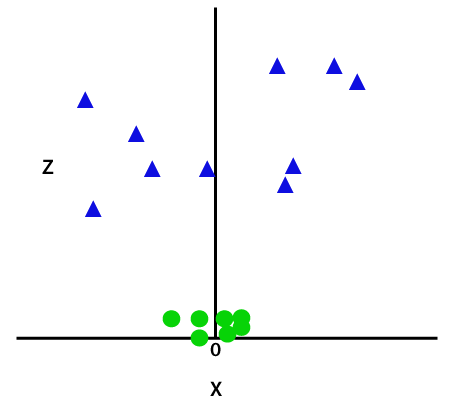
så nu delar SVM upp datauppsättningarna i klasser på följande sätt. Tänk på bilden nedan:
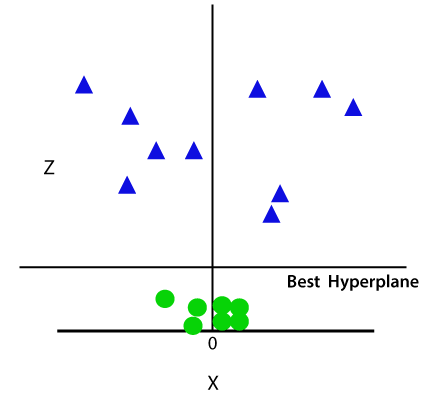
eftersom vi befinner oss i 3-D-utrymme ser det ut som ett plan parallellt med x-axeln. Om vi konverterar det i 2d-utrymme med z = 1 blir det som:
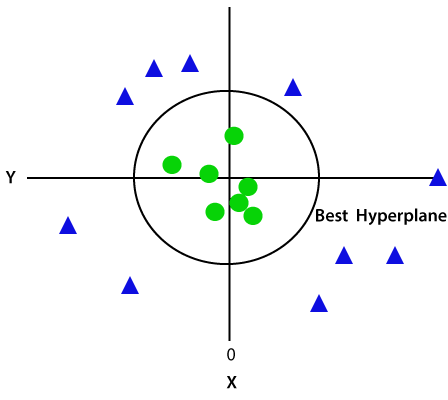
därför får vi en omkrets av radie 1 vid icke-linjära data.,
Python implementering av Supportvektormaskin
nu kommer vi att implementera SVM-algoritmen med Python. Här kommer vi att använda samma dataset user_data, som vi har använt i Logistisk regression och KNN klassificering.
- dataförbehandlingssteg
tills dataförbehandlingssteget kommer koden att förbli densamma. Nedan följer koden:
Efter att ha utfört ovanstående kod kommer vi att förbehandla data., Koden kommer att ge datauppsättningen som:
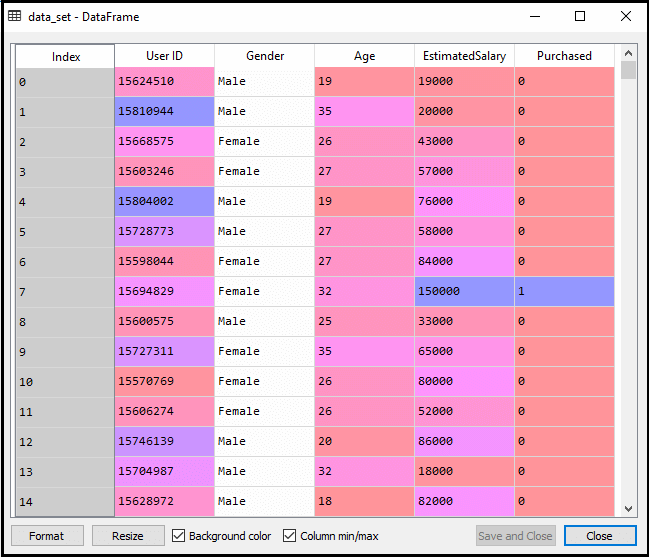
den skalade utmatningen för testuppsättningen kommer att vara:
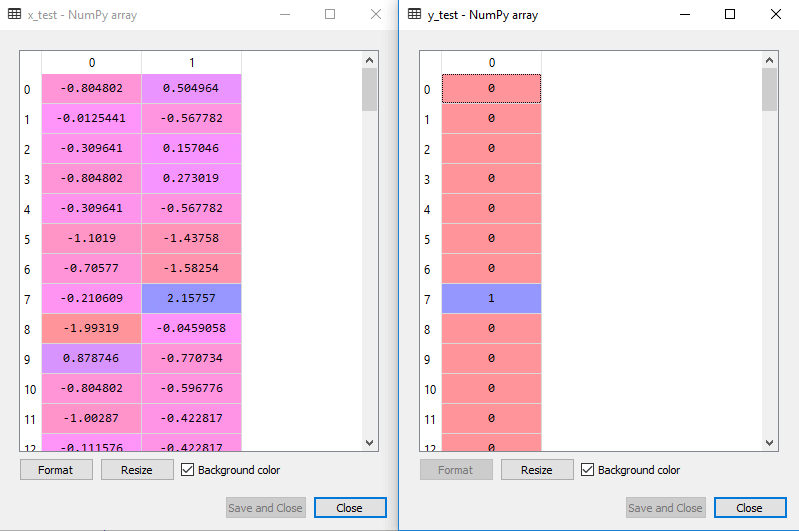
montering av SVM-klassificeraren till träningsuppsättningen:
nu kommer träningsuppsättningen att monteras på SVM-klassificeraren. För att skapa SVM-klassificeraren importerar vi SVC-klassen från Sklearn.SVM bibliotek. Nedan följer koden för den:
i ovanstående kod har vi använt kernel=’linear’, som här skapar vi SVM för linjärt separerbar data. Vi kan dock ändra det för icke-linjära data., Och sedan passade vi klassificeraren till träningsdataset(x_train, y_train)
utgång:
modellens prestanda kan ändras genom att ändra värdet på C (Regulariseringsfaktor), gamma och kärna.
- förutsäga test set resultat:
Nu kommer vi att förutsäga utdata för test set. För detta kommer vi att skapa en ny vektor y_pred. Nedan följer koden för den:
Efter att ha fått y_pred-vektorn kan vi jämföra resultatet av y_pred och y_test för att kontrollera skillnaden mellan det faktiska värdet och det förutsagda värdet.,
utdata: nedan är utdata för förutsägelsen av testuppsättningen:

- skapa förvirringsmatrisen:
Nu kommer vi att se prestandan hos SVM-klassificeraren att hur många felaktiga förutsägelser finns jämfört med den logistiska regressionsklassificeraren. För att skapa förvirringsmatrisen måste vi importera funktionen confusion_matrix i sklearn-biblioteket. Efter att ha importerat funktionen kallar vi den med en ny variabel cm. Funktionen tar två parametrar, främst y_true (de faktiska värdena) och y_pred (den riktade värderetur av klassificeraren)., Nedan följer koden för den:
utgång:
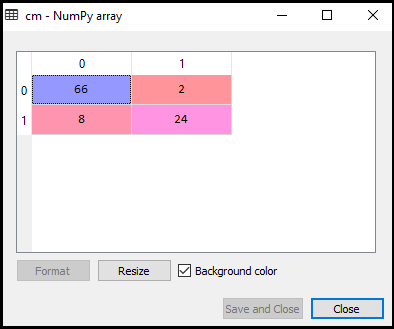
som vi kan se i ovanstående utmatningsbild finns 66+24= 90 korrekta förutsägelser och 8+2= 10 korrekta förutsägelser. Därför kan vi säga att vår SVM-modell förbättrades jämfört med logistisk regressionsmodell.,
- visualisera träningsresultatet:
Nu kommer vi att visualisera träningsresultatet, nedan är koden för det:
Output:
genom att köra ovanstående kod kommer vi att få utdata som:
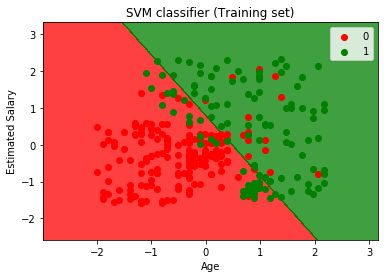
som vi kan se visas ovanstående utmatning som liknar den logistiska regressionsutgången. I utgången fick vi den raka linjen som hyperplane eftersom vi har använt en linjär kärna i klassificeraren. Och vi har också diskuterat ovan att för 2d-rymden är hyperplanet i SVM en rak linje.,
- visualisera testresultatet:
Output:
genom att köra ovanstående kod får vi utdata som:
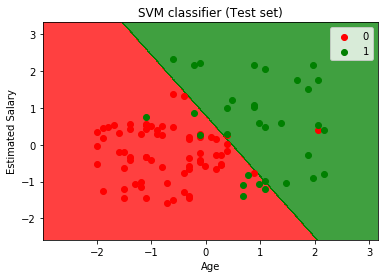
som vi kan se i ovanstående utdatabild har SVM-klassificeraren delat användarna i två regioner (köpt eller inte köpt). Användare som köpte SUV är i den röda regionen med de röda scatter-punkterna. Och användare som inte köpte SUV är i den gröna regionen med gröna scatter-poäng. Hyperplane har delat upp de två klasserna i köpt och inte köpt variabel.