antagande om normalitet för den beroende variabeln
det oberoende T-testet kräver att den beroende variabeln är ungefär normalt fördelad inom varje grupp.
Obs! tekniskt sett är det de residualer som normalt måste distribueras, men för ett oberoende t-test kommer båda att ge dig samma resultat.,
Du kan testa för detta med ett antal olika tester, men Shapiro-Wilks – testet av normalitet eller en grafisk metod, som en Q-Q-Plot, är mycket vanliga. Du kan köra dessa tester med hjälp av SPSS Statistik, det förfarande som kan hittas i vår test för normalitet guide. T-testet beskrivs dock som ett robust test med avseende på antagandet om normalitet. Detta innebär att en viss avvikelse från normalitet inte har ett stort inflytande på typ i felfrekvenser. Undantaget från detta är om förhållandet mellan den minsta och största gruppstorleken är större än 1.,5 (största jämfört med minsta).
vad du ska göra när du bryter mot normalitet antagande
om du upptäcker att antingen en eller båda av din grupps data inte är ungefär normalt fördelade och grupper storlekar skiljer sig kraftigt, har du två alternativ: (1) omvandla dina data så att data blir normalt fördelade (för att göra detta i SPSS Statistik se vår guide om att omvandla Data), eller (2) Kör Mann-Whitney U test som är en icke-parametrisk test som inte kräver antagandet om normalitet (för att köra detta test i SPSS Statistik se vår guide på Mann-Whitney U test).,
antagande om homogenitet av varians
det oberoende T-testet förutsätter varianterna hos de två grupperna som du mäter är lika i befolkningen. Om dina avvikelser är ojämna kan detta påverka typ i-felfrekvensen. Antagandet om homogenitet av varians kan testas med hjälp av Levenes Test av jämlikhet av varianser, som produceras i SPSS-Statistik när man kör det oberoende t-testförfarandet., Om du har kört Levenes test av jämlikhet av varianser i SPSS-statistiken får du ett resultat som liknar det nedan:

detta test för homogenitet av varians ger ett f-statistik och ett signifikansvärde (p-värde). Vi är främst oroade över signifikansvärdet – om det är större än 0,05 (dvs p > .05), våra gruppvarianser kan behandlas som lika. Men om p < 0.05 har vi ojämlika variationer och vi har brutit mot antagandet om homogenitet av varianser.,
övervinna en överträdelse av antagandet om homogenitet av varians
om Levens Test för jämlikhet av varianser är statistiskt signifikant, vilket indikerar att gruppvariationerna är ojämlika i befolkningen, kan du korrigera för denna överträdelse genom att inte använda den poolade uppskattningen för felperioden för t-statistiken, utan istället använda en justering av frihetsgraden med hjälp av Welch-Satterthwaite-metoden., I hela verkligheten kommer du förmodligen aldrig att ha hört talas om dessa justeringar eftersom SPSS-statistiken döljer denna information och helt enkelt markerar de två alternativen som ”lika avvikelser antagna” och ”lika avvikelser som inte antas” utan att uttryckligen ange de underliggande testerna som används., Du kan dock se bevisen för dessa tester enligt nedan:
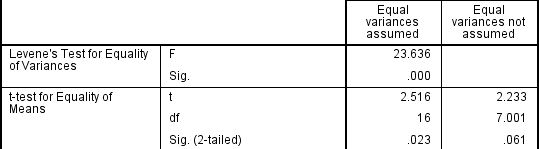
från resultatet av Levenes Test för jämlikhet av varianser kan vi avvisa nollhypotesen att det inte finns någon skillnad i varianterna mellan grupperna och acceptera den alternativa hypotesen att det finns en statistiskt signifikant skillnad i varianterna mellan grupperna., Effekten av att inte kunna anta lika variationer är uppenbar i den sista kolumnen i ovanstående figur där vi ser en minskning av värdet av t-statistiken och en stor minskning av frihetsgraderna (df). Detta har effekten att öka p-värdet över den kritiska signifikansnivån på 0,05. I det här fallet accepterar vi därför inte den alternativa hypotesen och accepterar att det inte finns några statistiskt signifikanta skillnader mellan medel. Detta skulle inte ha varit vår slutsats om vi inte hade testat för homogenitet av varianser.