introduktion
linjär regression, även känd som enkel linjär regression eller bivariat linjär regression, används när vi vill förutsäga värdet av en beroende variabel baserat på värdet av en oberoende variabel. Du kan till exempel använda linjär regression för att förstå om examensresultat kan förutsägas baserat på revisionstid (dvs.,, din beroende variabel skulle vara ”exam performance”, mätt från 0-100 märken, och din oberoende variabel skulle vara ”revisionstid”, mätt i timmar). Alternativt kan du använda linjär regression för att förstå om cigarettförbrukningen kan förutsägas baserat på rökningens varaktighet (dvs din beroende variabel skulle vara ”cigarettförbrukning”, mätt i antalet cigaretter som konsumeras dagligen och din oberoende variabel skulle vara ”rökningens varaktighet”, mätt i dagar). Om du har två eller flera oberoende variabler, snarare än bara en, måste du använda flera regression., Alternativt, om du bara vill fastställa om ett linjärt förhållande finns, kan du använda Pearsons korrelation.
Obs: den beroende variabeln kallas också utfall, mål eller kriterium variabel, medan den oberoende variabeln också kallas prediktor, förklarande eller regressor variabel. I slutändan, oavsett vilken term du använder, är det bäst att vara konsekvent. Vi kommer att hänvisa till dessa som beroende och oberoende variabler i hela denna guide.,
i den här guiden visar vi hur du utför linjär regression med Stata, samt tolka och rapportera resultaten från detta test. Men innan vi introducerar dig till denna procedur måste du förstå de olika antaganden som dina data måste uppfylla för att linjär regression ska ge dig ett giltigt resultat. Vi diskuterar dessa antaganden nästa.
stata
antaganden
det finns sju ”antaganden” som ligger till grund för linjär regression. Om någon av dessa sju antaganden inte uppfylls kan du inte analysera dina data med linjär eftersom du inte får ett giltigt resultat., Eftersom antaganden # 1 och #2 relaterar till ditt val av variabler, kan de inte testas för att använda Stata. Du bör dock bestämma om din studie uppfyller dessa antaganden innan du går vidare.
- antagande #1: DIN beroende variabel ska mätas på kontinuerlig nivå., Exempel på sådana kontinuerliga variabler är höjd (mätt i fot och tum), temperatur (mätt i oC), lön (mätt i US-Dollar), revisionstid (mätt i timmar), intelligens (mätt med IQ-poäng), reaktionstid (mätt i millisekunder), testprestanda (mätt från 0 till 100), försäljning (mätt i antal transaktioner per månad) och så vidare. Om du är osäker på om din beroende variabel är kontinuerlig (d.v. s. mätt vid intervallet eller förhållandet nivå), se våra typer av variabel guide.,
- antagande #2: din oberoende variabel ska mätas på kontinuerlig eller kategorisk nivå. Men om du har en kategorisk oberoende variabel är det vanligare att använda ett oberoende t-test (för 2 grupper) eller envägsanova (för 3 grupper eller mer). Om du är osäker, exempel på kategoriska variabler inkluderar kön (t. ex. 2 grupper: manliga och kvinnliga), etnicitet (t. ex. 3 grupper: kaukasiska, afroamerikanska och latinamerikanska), fysisk aktivitetsnivå (t. ex. 4 grupper: stillasittande, låg, måttlig och hög), och yrke (t. ex.,, 5 grupper: kirurg, läkare, sjuksköterska, tandläkare, terapeut). I den här guiden visar vi dig linjär regressionsförfarande och Stata-utgång när både dina Beroende och oberoende variabler mättes på en kontinuerlig nivå.
lyckligtvis kan du kontrollera antaganden #3, #4, #5, #6 och # 7 med Stata. När man går vidare till antaganden #3, #4, #5, #6 och # 7, Vi föreslår att du testar dem i den här ordningen eftersom den representerar en order där du inte längre kan använda linjär regression om en överträdelse av antagandet inte är korrigerbar., I själva verket, bli inte förvånad om dina data misslyckas en eller flera av dessa antaganden eftersom detta är ganska typiskt när man arbetar med verkliga data snarare än lärobok exempel, som ofta bara visar dig hur man utför linjär regression när allt går bra. Men oroa dig inte eftersom även när dina data misslyckas vissa antaganden, det finns ofta en lösning för att övervinna detta (t.ex. omvandla dina data eller använda en annan statistisk test istället)., Kom bara ihåg att om du inte kontrollerar att du data uppfyller dessa antaganden eller om du testar för dem felaktigt, kan resultaten du får när du kör linjär regression inte vara giltiga.
- antagande #3: Det måste finnas ett linjärt förhållande mellan de beroende och oberoende variablerna. Även om det finns ett antal sätt att kontrollera om det finns ett linjärt förhållande mellan dina två variabler, föreslår vi att du skapar en scatterplot med Stata, där du kan rita den beroende variabeln mot din oberoende variabel., Du kan sedan visuellt inspektera scatterplot för att kontrollera linjäritet. Din scatterplot kan se ut som något av följande:
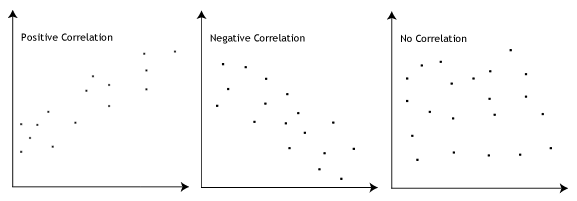
om relationen som visas i din scatterplot inte är linjär måste du antingen köra en icke-linjär regressionsanalys eller ”omvandla” dina data, som du kan göra med Stata.
- antagande #4: Det bör inte finnas några signifikanta avvikare. Outliers är helt enkelt enstaka datapunkter i dina data som inte följer det vanliga mönstret (t. ex.,, i en studie av 100 elevernas IQ-poäng, där medelvärdet var 108 med endast en liten variation mellan studenter, hade en student en poäng på 156, vilket är mycket ovanligt, och kan till och med sätta henne i topp 1% av IQ-poäng globalt). Följande scatterplots markerar den potentiella effekten av avvikare:
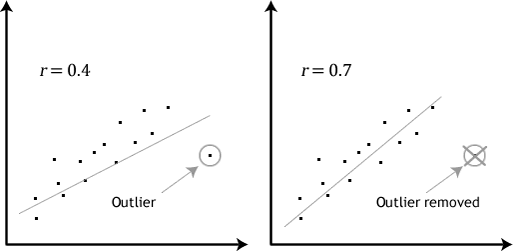
problemet med avvikare är att de kan ha en negativ effekt på regressionsekvationen som används för att förutsäga värdet av den beroende variabeln baserat på den oberoende variabeln., Detta kommer att ändra produktionen som Stata producerar och minska den prediktiva noggrannheten i dina resultat. Lyckligtvis kan du använda Stata för att utföra casewise diagnostik för att hjälpa dig att upptäcka eventuella outliers.
- antagande #5: Du bör ha oberoende av observationer, som du enkelt kan kontrollera med Durbin-Watson statistik, vilket är ett enkelt test för att köra med Stata.
- antagande #6: dina data måste visa homoscedasticitet, vilket är där varianterna längs linjen med bästa passform förblir likartade när du rör dig längs linjen., De två scatterplots nedan ger enkla exempel på data som uppfyller detta antagande och en som misslyckas antagandet:
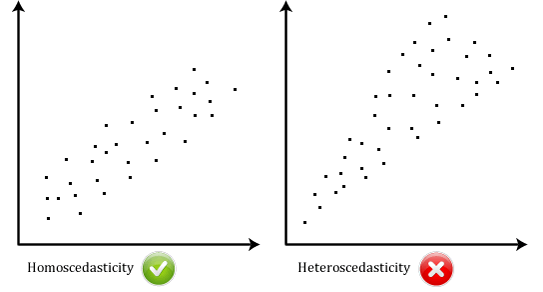
När du analyserar dina egna data kommer du att ha tur om din scatterplot ser ut som någon av de två ovan. Även om dessa hjälper till att illustrera skillnaderna i data som möter eller bryter mot antagandet om homoscedasticitet, är verkliga data ofta mycket mer rörigt., Du kan kontrollera om dina data visade homoscedasticitet genom att rita regressionsstandardiserade residualer mot det regressionsstandardiserade förutspådda värdet.
- antagande #7: Slutligen måste du kontrollera att residualerna (fel) i regressionslinjen är ungefär normalt fördelade. Två vanliga metoder för att kontrollera detta antagande innefattar att använda antingen ett histogram (med en överlagrad normal kurva) eller en Normal P-P-Plot.
i praktiken kontrollerar man antaganden #3, #4, #5, #6 och # 7 kommer förmodligen att ta upp det mesta av din tid när du utför linjär regression., Det är dock inte en svår uppgift, och Stata ger alla verktyg du behöver göra detta.
i avsnittet procedur illustrerar vi Stata-proceduren som krävs för att utföra linjär regression förutsatt att inga antaganden har kränkts. För det första redogjorde vi för det exempel vi använder för att förklara det linjära regressionsförfarandet i Stata.
Stata
exempel
studier visar att träning kan bidra till att förebygga hjärtsjukdomar. Inom rimliga gränser, ju mer du tränar, desto mindre risk har du att lida av hjärtsjukdom., Ett sätt på vilket motion minskar risken för att drabbas av hjärtsjukdomar är genom att minska ett fett i blodet, som kallas kolesterol. Ju mer du tränar desto lägre kolesterolkoncentration. Dessutom har det nyligen visat sig att den tid du spenderar på att titta på TV – en indikator på en stillasittande livsstil – kan vara en bra prediktor för hjärtsjukdom (dvs Ju mer TV du tittar desto större är risken för hjärtsjukdom).,
därför bestämde en forskare att avgöra om kolesterolkoncentrationen var relaterad till tid som spenderades på att titta på TV i annars friska 45 till 65 år gamla män (en riskkategori av människor). Till exempel, som människor spenderade mer tid på att titta på TV, ökade deras kolesterolkoncentration också (ett positivt förhållande); eller hände motsatsen? Forskaren ville också veta andelen kolesterolkoncentration som tiden som spenderas på att titta på TV kan förklara, liksom att kunna förutsäga kolesterolkoncentration., Forskaren kunde sedan avgöra om till exempel personer som spenderade åtta timmar på att titta på TV per dag hade farligt höga kolesterolkoncentrationer jämfört med personer som tittade på bara två timmars TV.
för att utföra analysen rekryterade forskaren 100 friska manliga deltagare mellan 45 och 65 år. Mängden tid som spenderades på att titta på TV (dvs den oberoende variabeln, time_tv) och kolesterolkoncentrationen (dvs den beroende variabeln, kolesterol) registrerades för alla 100-deltagare., Uttryckt i varierande termer ville forskaren regressera kolesterol på time_tv.
Obs! exemplet och data som används för den här guiden är fiktiva. Vi har just skapat dem för syftet med denna guide.
stata
inställning i Stata
Obs: Det spelar ingen roll om du skapar den beroende eller oberoende variabeln först.
Efter att ha skapat dessa två variabler – time_tv och kolesterol – skrev vi in poängen för var och en i de två kolumnerna i dataredigeraren (redigera) kalkylblad (dvs.,, den tid i timmar som deltagarna tittade på TV i den vänstra kolumnen (dvs time_tv, den oberoende variabeln) och deltagarnas kolesterolkoncentration i mmol/l i den högra kolumnen (dvs kolesterol, den beroende variabeln), som visas nedan:
publicerad med skriftligt tillstånd från StataCorp LP.,
Stata
testförfarande i Stata
i det här avsnittet visar vi hur du analyserar dina data med linjär regression i Stata när de sex antagandena i föregående avsnitt, antaganden, inte har kränkts. Du kan utföra linjär regression med hjälp av kod eller statas grafiska användargränssnitt (GUI). När du har utfört din analys visar vi hur du tolkar dina resultat. Välj först om du vill använda kod eller statas grafiska användargränssnitt (GUI).,
kod
koden för att utföra linjär regression på dina data tar formen:
regress DependentVariable IndependentVariable
denna kod anges i rutan nedan:
publicerad med skriftligt tillstånd från statacorp lp.,
med hjälp av vårt exempel där den beroende variabeln är kolesterol och den oberoende variabeln är time_tv, skulle den önskade koden vara:
regress cholesterol time_tv
Obs 1: Du måste vara exakt när du anger koden i rutan. Koden är ”skiftlägeskänslig”. Till exempel, om du angett ”kolesterol” där ” C ” är versaler snarare än gemener (dvs, ett felmeddelande som följande:
Obs 2: Om du fortfarande får felmeddelandet i Not 2: ovan är det värt att kontrollera namnet du gav dina två variabler i Dataredigeraren när du konfigurerar filen (dvs. se Dataredigeringsskärmen ovan)., I rutan till höger på skärmen Dataredigerare är det så att du stavat dina variabler i avsnittet
, inte avsnittet
som du måste ange i koden (se nedan för vår beroende variabel). Detta kan tyckas uppenbart, men det är ett fel som ibland görs, vilket resulterar i felet i Not 2 ovan.
Skriv därför in koden, regress cholesterol time_tv och tryck på ”Return/Enter” – knappen på tangentbordet.,
publicerad med skriftligt tillstånd från StataCorp LP.
Du kan se stata-utgången som kommer att produceras här.,
grafiskt användargränssnitt (GUI)
de tre steg som krävs för att utföra linjär regression i Stata 12 och 13 visas nedan:
- Klicka på statistik > linjära modeller och relaterade > linjär regression på huvudmenyn, som visas nedan:
publicerad med skriftligt tillstånd från statacorp lp.,
Du kommer att presenteras med dialogrutan Regress – Linear regression:
publicerad med skriftligt tillstånd från StataCorp LP.
- Välj kolesterol inifrån den beroende variabeln: rullgardinsmenyn och time_tv inifrån den oberoende variabeln: rullgardinsmenyn. Du kommer att sluta med följande skärm:
publicerad med skriftligt tillstånd från StataCorp LP.,
-
klicka på knappen
. Detta kommer att generera utdata.
Stata
utgång av linjär regressionsanalys i Stata
om dina data passerade antagande # 3 (dvs det fanns ett linjärt förhållande mellan dina två variabler), #4 (dvs det fanns inga signifikanta avvikare), antagande #5 (dvs du hade oberoende av observationer), antagande #6 (dvs dina data visade homoscedasticitet) och antagande #7 (dvs.,, residualerna (fel) var ungefär normalt distribuerade), som vi förklarade tidigare i avsnittet antaganden, behöver du bara tolka följande linjära regressionsutgång i Stata:
publicerad med skriftligt tillstånd från StataCorp LP.,
utdata består av fyra viktiga delar av information: (a) R2-värdet (”R-squared” – raden) representerar andelen varians i den beroende variabeln som kan förklaras av vår oberoende variabel (tekniskt är det andelen variation som redovisas av regressionsmodellen ovan och bortom medelmodellen). R2 är dock baserat på provet och är en positivt partisk uppskattning av andelen av variansen hos den beroende variabeln som redovisas av regressionsmodellen (dvs., R2-värdet (”Adj R-squared” – raden), som korrigerar positiv bias för att ge ett värde som skulle förväntas i befolkningen, c) F-värdet, frihetsgrader (”F( 1, 98)”) och statistisk signifikans för regressionsmodellen (”Prob > f” – raden) och d) koefficienterna för den konstanta och oberoende variabeln (”Coef.”kolumn), som är den information du behöver för att förutsäga den beroende variabeln, kolesterol, med hjälp av den oberoende variabeln, time_tv.
i det här exemplet, R2 = 0.151. Justerat R2 = 0,143 (till 3 D.P.,), vilket innebär att den oberoende variabeln, time_tv, förklarar 14,3% av variationen hos den beroende variabeln, kolesterol, i befolkningen. Justerat R2 är också en uppskattning av effektstorleken, som vid 0,143 (14,3%), är en indikation på en medelstor effekt, enligt Cohens (1988) klassificering. Normalt är det dock R2 som inte är den justerade R2 som rapporteras i resultat. I detta exempel är regressionsmodellen statistiskt signifikant, F (1, 98) = 17,47, p = .0001., Detta indikerar att den övergripande modellen som används statistiskt signifikant kan förutsäga den beroende variabeln kolesterol.
Obs! vi presenterar resultatet från den linjära regressionsanalysen ovan. Men eftersom du borde ha testat dina data för de antaganden vi förklarade tidigare i Antagandesektionen måste du också tolka Stata-produktionen som producerades när du testade för dessa antaganden. Detta inkluderar: (a) de scatterplots du använde för att kontrollera om det fanns ett linjärt samband mellan dina två variabler (dvs.,, Antagande #3); (b) casewise-diagnostik för att kontrollera att det inte fanns inga signifikanta outliers (dvs. Antagandet #4); (c) produktionen från Durbin-Watson statistik för att kontrollera för oberoende observationer (dvs. Antagandet #5); (d) en scatterplot av regression standardiserade residualerna mot den regression standardiserade förväntade värdet för att avgöra om din data visade homoscedasticity (dvs. Antagandet #6), och ett histogram (med överlagrade normala kurvan) och Normala P-P Komplott för att kontrollera om residualerna (fel) var ungefär normalfördelad (dvs. Antagandet #7)., Kom också ihåg att om dina data misslyckades med någon av dessa antaganden kommer den produktion som du får från det linjära regressionsförfarandet (dvs. den produktion vi diskuterar ovan) inte längre att vara relevant, och du kan behöva utföra ett annat statistiskt test för att analysera dina data.,
Stata
rapporterar utdata från linjär regressionsanalys
När du rapporterar utdata från din linjära regression är det bra att inkludera: (a) en introduktion till den analys du utförde; (B) information om ditt prov, inklusive eventuella saknade värden; (c) det observerade F-värdet, graden av frihet och signifikansnivå (dvs. p-värdet); (d) den procentuella variabiliteten i den beroende variabeln som förklaras av den oberoende variabeln (dvs. din justerade R2-värde).); och (e) regressionsekvationen för din modell., Baserat på resultaten ovan kunde vi rapportera resultaten av denna studie enligt följande:
- allmänt
en linjär regression fastställde att daglig tid som spenderas på att titta på TV statistiskt signifikant kunde förutsäga kolesterolkoncentrationen, F (1, 98) = 17.47, p = .0001 och tid att titta på TV stod för 14,3% av den förklarade variationen i kolesterolkoncentrationen. Regressionsekvationen var: förväntad kolesterolkoncentration = -2.135 + 0.044 x (tid som spenderas på att titta på tv).,
förutom att rapportera resultaten enligt ovan kan ett diagram användas för att visuellt presentera dina resultat. Till exempel, Du kan göra detta med hjälp av en scatterplot med förtroende och förutsägelse intervall (även om det inte är mycket vanligt att lägga till den sista). Detta kan göra det lättare för andra att förstå dina resultat. Dessutom kan du använda din linjära regressionsekvation för att göra förutsägelser om värdet av den beroende variabeln baserat på olika värden för den oberoende variabeln., Även om Stata inte producerar dessa värden som en del av det linjära regressionsförfarandet ovan, finns det ett förfarande i Stata som du kan använda för att göra det.