vi klassiskt tänker på ljus som alltid reser i raka linjer, men när ljusvågor passerar nära en barriär tenderar de att böja sig runt den barriären och bli utspridda. Diffraktion av ljus uppstår när en ljusvåg passerar genom ett hörn eller genom en öppning eller slits som är fysiskt den ungefärliga storleken på, eller ännu mindre än det ljusets våglängd.,

en mycket enkel demonstration av diffraktion kan utföras genom att hålla handen framför en ljuskälla och långsamt stänga två fingrar samtidigt observera det ljus som överförs mellan dem. När fingrarna närmar sig varandra och kommer mycket nära varandra börjar du se en serie mörka linjer parallellt med fingrarna. De parallella linjerna är faktiskt diffraktionsmönster. Detta fenomen kan också uppstå när ljuset är ”böjt” runt partiklar som är i samma storleksordning som ljusets våglängd., Ett bra exempel på detta är diffraktionen av solljus av moln som vi ofta hänvisar till som en silverfoder, illustrerad i Figur 1 med en vacker solnedgång över havet.
Vi kan ofta observera pastellfärger av blått, rosa, lila och grönt i moln som genereras när ljuset diffrakteras från vattendroppar i molnen. Mängden diffraktion beror på ljusets våglängd, med kortare våglängder diffraherade i en större vinkel än längre (i själva verket diffrakteras blått och violett ljus i en högre vinkel än rött ljus)., När en ljusvåg som färdas genom atmosfären möter en droppe vatten, som illustreras nedan, bryts den först vid vattnet: luftgränssnittet, då reflekteras det som det igen möter gränssnittet. Strålen, som fortfarande reser inuti vattendroppen, bryts återigen när den träffar gränssnittet för en tredje gång. Denna sista interaktion med gränssnittet bryter ljuset tillbaka in i atmosfären, men det skiljer också en del av ljuset som illustreras nedan., Detta diffraktionselement leder till ett fenomen som kallas Cellinis halo (även känd som Heiligenschein-effekten) där en ljus ring av ljus omger skuggan av observatörens Huvud.
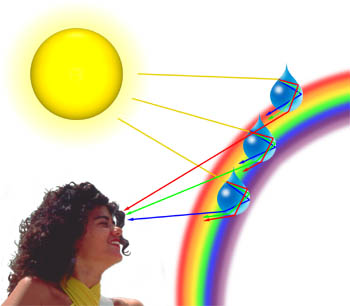
termerna diffraktion och spridning används ofta omväxlande och anses vara nästan synonymt. Diffraktion beskriver ett specialfall av ljusspridning där ett objekt med regelbundet återkommande funktioner (som ett diffraktionsgitter) ger en ordnad diffraktion av ljus i ett diffraktionsmönster., I den verkliga världen är de flesta objekt mycket komplexa i form och bör anses vara sammansatt av många individuella diffraktionsegenskaper som kollektivt kan producera en slumpmässig spridning av ljus.
ett av de klassiska och mest grundläggande begreppen som involverar diffraktion är det enda slitna optiska diffraktionsexperimentet, som först genomfördes i början av artonhundratalet. När en ljusvåg sprids genom en slits (eller bländare) beror resultatet på bländarens fysiska storlek med avseende på våglängden hos den infallande strålen., Detta illustreras i Figur 3 om man antar en sammanhängande, monokromatisk våg som avges från punktkällan S, som liknar ljus som skulle produceras av en laser, passerar genom bländare d och diffraheras, med den primära infallande ljusstrålen landning vid punkt P och den första sekundära maxima inträffar vid punkt Q.
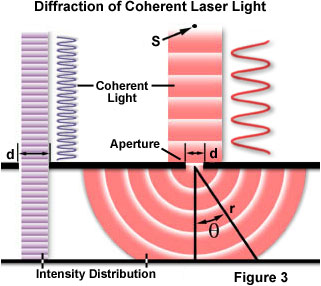
som visas i den vänstra sidan av figuren, när våglängden (λ) är mycket mindre än bländarbredden (d), vågen färdas helt enkelt vidare i en rak linje, precis som det skulle om det var en partikel eller ingen bländare var närvarande., Men när våglängden överstiger bländarens storlek upplever vi diffraktion av ljuset enligt ekvationen:
där θ är vinkeln mellan den infallande centrala utbredningsriktningen och det första minsta av diffraktionsmönstret. Experimentet ger en ljus central maximum som flankeras på båda sidor av sekundär maxima, med intensiteten av varje efterföljande sekundär maximum minskar när avståndet från centrum ökar. Figur 4 illustrerar denna punkt med en plot av strålintensitet kontra diffraktionsradie., Observera att minima som förekommer mellan sekundära maxima är belägna i multiplar av π.
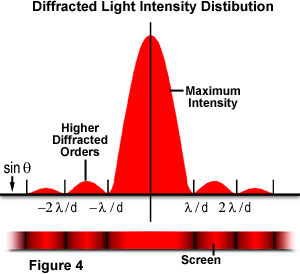
detta experiment förklarades först av Augustin Fresnel som tillsammans med Thomas Young framförde viktiga bevis för att ljuset färdas i vågor. Från figurerna ovan ser vi hur ett sammanhängande, monokromatiskt ljus (i detta exempel laserbelysning) som emitteras från punkt L diffrakteras av bländare d., Fresnel antog att amplituden för den första ordningen maxima vid punkt Q(definierad som eQ) skulle ges med ekvationen:
där A är amplituden för den infallande vågen, r är avståndet mellan D och Q, och f (χ) är en funktion av χ, En lutningsfaktor introducerad av Fresnel.
diffraktion av ljus
utforska hur en ljusstråle diffraheras när den passerar genom en smal slits eller bländare. Justera våglängden och bländarstorleken och observera hur detta påverkar diffraktionsintensitetsmönstret.,
diffraktion av ljus spelar en viktig roll för att begränsa upplösningseffekten hos något optiskt instrument (till exempel: kameror, kikare, teleskop, mikroskop och ögat). Lösningseffekten är det optiska instrumentets förmåga att producera separata bilder av två intilliggande punkter. Detta bestäms ofta av kvaliteten på linserna och speglarna i instrumentet samt egenskaperna hos det omgivande mediet (vanligtvis luft). Ljusets vågliknande natur tvingar en ultimat gräns för alla optiska instruments lösande kraft.,
våra diskussioner om diffraktion har använt en slits som bländaren genom vilken ljuset diffraheras. Alla optiska instrument har emellertid cirkulära öppningar, till exempel pupillen i ett öga eller det cirkulära membranet och linserna i ett mikroskop. Cirkulära öppningar producerar diffraktionsmönster som liknar de som beskrivits ovan, förutom att mönstret naturligt uppvisar en cirkulär symmetri. Matematisk analys av diffraktionsmönstren som produceras av en cirkulär bländare beskrivs av ekvationen:
där θ (1) är vinkelläget för första ordningens diffraktionsminima (den första mörka ringen), λ är våglängden för det infallande ljuset, D är bländarens diameter och 1,22 är en konstant. Under de flesta omständigheter, vinkeln θ (1) är mycket liten så approximationen att synden och tan av vinkeln är nästan lika utbyten:
från dessa ekvationer blir det uppenbart att den centrala maximum är direkt proportionell mot λ/d gör detta maximum mer utspridda för längre våglängder och för mindre öppningar., Den sekundära mimina av diffraktion satt en gräns för den användbara förstoringen av objektiva linser i optisk mikroskopi, på grund av inneboende diffraktion av ljus av dessa linser. Oavsett hur perfekt linsen kan vara, är bilden av en punktkälla av ljus som produceras av linsen åtföljd av sekundär och högre ordning maxima. Detta kan elimineras endast om linsen hade en oändlig diameter. Två objekt separerade med ett avstånd mindre än θ (1) kan inte lösas, oavsett hur hög kraften i förstoring., Medan dessa ekvationer härleddes för bilden av en punkt ljuskälla ett oändligt avstånd från bländaren, är det en rimlig approximation av lösningseffekten hos ett mikroskop när d ersätts med objektivlinsens diameter.
om två objekt bor ett avstånd D från varandra och ligger på ett avstånd L från en observatör är vinkeln (uttryckt i radianer) mellan dem:
vilket leder oss till att kondensera de två sista ekvationerna för att ge:
där d(0) är det minsta separationsavståndet mellan objekten som gör det möjligt att lösa dem. Med hjälp av denna ekvation kan det mänskliga ögat lösa föremål separerade med ett avstånd av 0,056 millimeter, men fotoreceptorerna i näthinnan är inte tillräckligt nära för att tillåta denna grad av upplösning och 0,1 millimeter är ett mer realistiskt tal under normala omständigheter.
lösningseffekten hos optiska mikroskop bestäms av ett antal faktorer, inklusive de som diskuterats, men under de mest idealiska omständigheterna är detta nummer cirka 0,2 mikrometer., Detta nummer måste ta hänsyn till optisk inriktning av mikroskopet, linsens kvalitet, liksom de övervägande våglängderna av ljus som används för att avbilda provet. Även om det ofta inte är nödvändigt att beräkna den exakta lösa kraften i varje mål (och skulle vara ett slöseri med tid i de flesta fall), är det viktigt att förstå funktionerna i mikroskoplinser som de gäller för den verkliga världen.
bidragande författare
Mortimer Abramowitz – Olympus America, Inc. Två Corporate Center Med Bil., Melville, New York, 11747.
Michael W., Davidson – Nationella Höga Magnetfält Laboratorium, 1800 East Paul Dirac Dr, Florida State University, Tallahassee, Florida, 32310.