läranderesultat
- identifiera foci, hörn, axlar och centrum av en ellips.
- skriv ekvationer av ellipser centrerade vid ursprunget.
- skriv ekvationer av ellipser som inte är centrerade vid ursprunget.
en konisk sektion, eller konisk, är en form som härrör från att skära en höger cirkulär kon med ett plan. Vinkeln vid vilken planet skär konen bestämmer formen.,
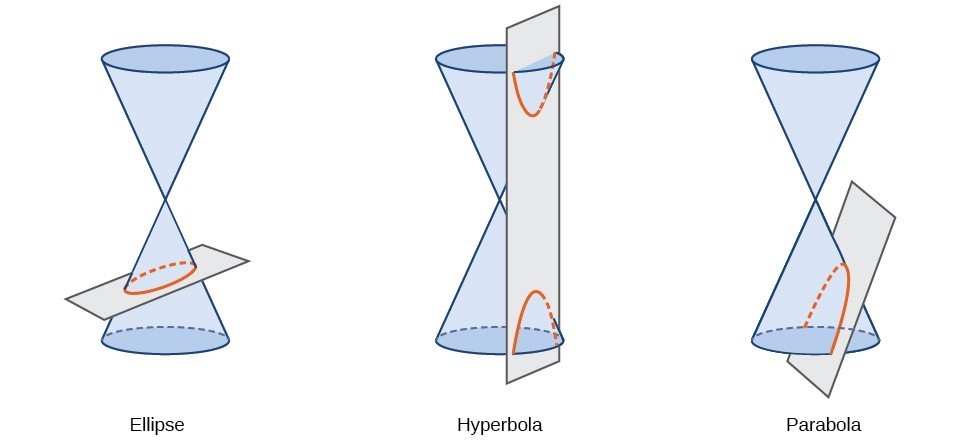
koniska sektioner kan också beskrivas med en uppsättning punkter i koordinatplanet. Senare i detta kapitel ser vi att grafen för någon kvadratisk ekvation i två variabler är en konisk sektion. Tecknen på ekvationerna och koefficienterna för de variabla termerna bestämmer formen. Detta avsnitt fokuserar på de fyra variationerna av standardformen för ekvationen för ellipsen. En ellips är uppsättningen av alla punkter \ vänster (x, y \ höger) i ett plan så att summan av deras avstånd från två fasta punkter är en konstant., Varje fast punkt kallas fokus (plural: foci) hos ellipsen.
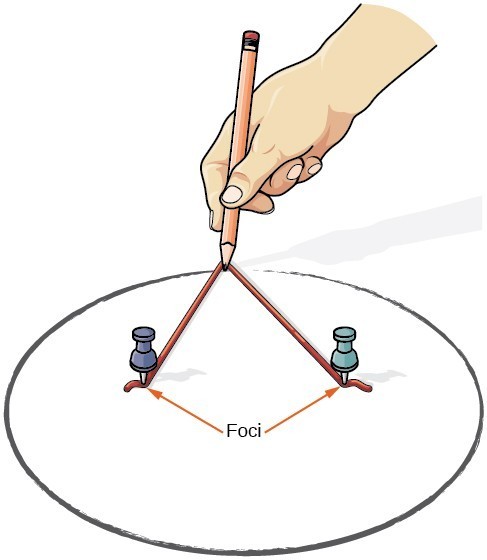
vi kan rita en ellips med en bit kartong, två häftstift, en penna och en sträng. Placera tummen i kartongen för att bilda ellipsens foci. Klipp en sträng längre än avståndet mellan de två tummen (strängens längd representerar konstanten i definitionen). Tack varje ände av strängen till kartongen, och spåra en kurva med en penna hålls spänd mot strängen. Resultatet är en ellips.
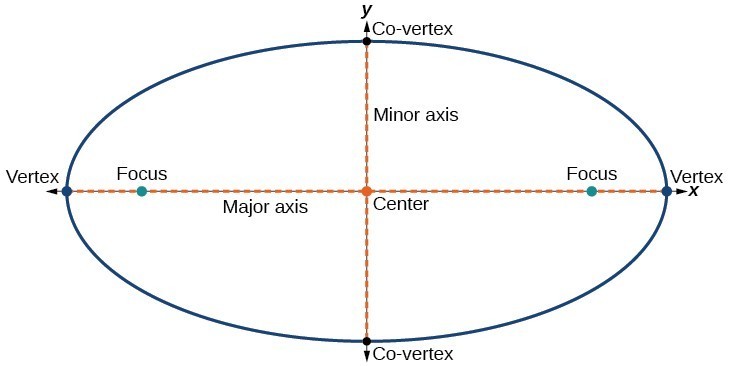
varje ellips har två symmetriaxlar., Den längre axeln kallas huvudaxeln, och den kortare axeln kallas den mindre axeln. Varje slutpunkt för huvudaxeln är ellipsens vertex (plural: vertices), och varje slutpunkt för den mindre axeln är en co-vertex av ellipsen. Mitten av en ellips är mittpunkten för både de stora och mindre axlarna. Axlarna är vinkelräta i mitten. Foci ligger alltid på huvudaxeln, och summan av avstånden från foci till vilken punkt som helst på ellipsen (den konstanta summan) är större än avståndet mellan foci.,
i det här avsnittet begränsar vi ellipser till de som är placerade vertikalt eller horisontellt i koordinatplanet. Det vill säga axlarna kommer antingen ligga på eller vara parallella med x– och y-axlarna. Senare i kapitlet kommer vi att se ellipser som roteras i koordinatplanet.
för att arbeta med horisontella och vertikala ellipser i koordinatplanet överväger vi två fall: de som är centrerade vid ursprunget och de som är centrerade vid en annan punkt än ursprunget., Först lär vi oss att härleda ellipsernas ekvationer, och då lär vi oss att skriva ellipsernas ekvationer i standardform. Senare kommer vi att använda vad vi lär oss att rita graferna.,v>om (x,y) är en punkt på ellipsen kan vi definiera följande variabler:
\begin{align}d_1&=\text{avståndet från } (-c, 0) \text{ till } (x,y) \\ d_2&= \text{avståndet från } (c,c,c,c, c, c, c, c, c, c, 0) \text{ to } (X, Y) \end{align}
\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1
för en ellips centrerad vid ursprunget med dess huvudaxel på x-axeln och
\dfrac{x^2}{b^2} 2}+\dfrac{y^2} {a^2}=1
för en ellips centrerad vid ursprunget med dess huvudaxel på Y-axeln.,
skriva ekvationer av ellipser som inte är centrerade vid ursprunget
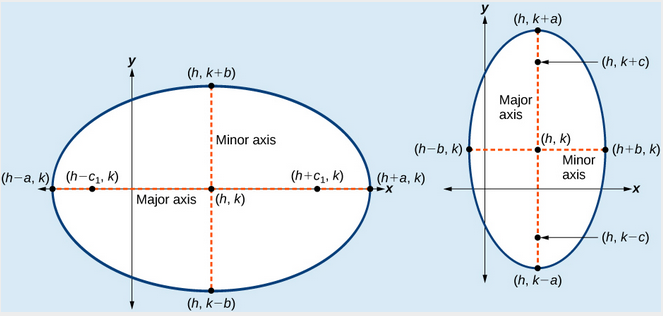
(a) horisontell ellips med center \left(H,k\right) (b) vertikal ellips med center \left(h,k\right)
lösa tillämpade problem med ellipser
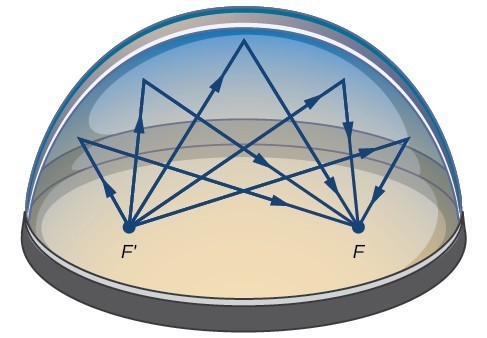
många real-världen situationer kan representeras av ellipser, inklusive banor av planeter, satelliter, månar och kometer, och former av båt kölar, roder, och vissa flygplan vingar. En medicinsk apparat som kallas lithotripter använder elliptiska reflektorer för att bryta upp njurstenar genom att generera ljudvågor., Vissa byggnader, som kallas whispering chambers, är utformade med elliptiska kupoler så att en person som viskar på ett fokus lätt kan höras av någon som står vid det andra fokuset. Detta beror på de akustiska egenskaperna hos en ellips. När en ljudvåg härstammar från ett fokus i en viskningskammare, kommer ljudvågen att reflekteras från den elliptiska kupolen och tillbaka till det andra fokuset. I whisperkammaren på Museum of Science and Industry i Chicago kan två personer som står vid foci—cirka 43 meter ifrån varandra—höra varandra viska.