detta är den första i en tre inlägg serie. Det andra inlägget talar omhur man beräknar Big-O. den tredje artikeln talar om att förståden formella definitionen av Big-O.
Big-O notation brukade vara ett riktigt läskigt koncept för mig. Jag tänkte på det här är hur” riktiga ” programmerare pratade om sin kod. Det var alltmer läskigt eftersom de akademiska beskrivningarna (som Wikipedia) gjorde mig väldigt liten mening. Detta är frustrerande eftersom de underliggande Concepts är faktiskt inte så svårt.,
enkelt uttryckt är Big-O notation hur programmerare pratar omalgoritmer. Algoritmer är ett annat skrämmande ämne som jag ska täcka inett annat inlägg, men för våra ändamål, låt oss säga att ”algoritm” betyder funktion i ditt program (vilket inte är för långt borta). En funktions Big-Onotation bestäms av hur den svarar på olika ingångar. Hur mycket långsammare är det om vi ger det en lista över 1000 saker att arbeta påi stället för en lista över 1 sak?
Tänk på den här koden:
def item_in_list(to_check, the_list): for item in the_list: if to_check == item: return True return False
så om vi kallar den här funktionen somitem_in_list(2, ) borde den vara ganska snabb., Vi slingrar över varje sak i listan och om vi hittadet första argumentet till vår funktion, returnera Sant. Om vi kommer till slutet och vi inte hittade det, returnera falskt.
”komplexiteten” för denna funktion ärO(n). Jag ska förklara vad dettabetyder på bara en sekund, men låt oss bryta ner denna mathematicalsyntax. O(n) läses ”Order of N” eftersom funktionenO också är känd som Orderfunktionen. Jag tror att det här beror på att vi gör approximation, som handlar om ”storleksordningar”.,
”storleksordningar” är ännu en matematisk term somgrundläggande berättar skillnaden mellan klasser av siffror. Tänk på skillnaden mellan 10 och 100. Om du Bild 10 av dina näravänner och 100 personer, det är en riktigt stor skillnad. På samma sätt är skillnaden mellan 1 000 och 10 000 ganska stor (i själva verket är skillnaden mellan en junker-bil och en lätt använd). Det visar sig att i approximation, så länge du är inom en storleksordning, du är ganska nära., Om du skulle gissa antalet gumballs i amachine, skulle du vara i storleksordning om du sa 200gumballs. 10.000 gumballs skulle vara långt borta.

Figur 1: en gumball maskin vars antal gumballs är förmodligen inom en storleksordning av 200.
Tillbaka till dissekera O(n) denna säger att om vi gör ett diagram av timeit tar att köra den här funktionen med olika storlek ingångar (t ex anarray av 1 objekt 2 objekt 3 objekt, etc), skulle vi se att itapproximately motsvarar det antal objekt som finns i arrayen., Detta kallas en linjär graf. Det betyder att linjen är i grunden rakom du skulle gradera den.
några av er kanske har fångat att om ouritem i kodprovet ovan alltid var det första objektet i listan, skulle vår kod vara verkligenfast! Detta är sant, men Big-O handlar om det ungefärliga värsta falletprestanda att göra något. Det värsta fallet för koden ovan är att det vi söker efter inte finns i listan alls. (Obs! matematiktermen för detta är ”övre gräns”, vilket betyder att det talar omDen matematiska gränsen för awfulness).,
om du ville se en graf för dessa funktioner ignorerar du funktionenO()och ändrar variabelnn förx. Du kan sedan skriva det i Wolfram Alpha som ”plot x” som visar dig en diagonalline. Anledningen till att du byter ut n för x är att deras grafprogram x som variabelnamn eftersom det motsvarar xaxis. X-axeln blir större från vänster till höger motsvarar attge större och större arrays till din funktion., Y-axisrepresenterar tid, så ju högre linjen desto långsammare är den.
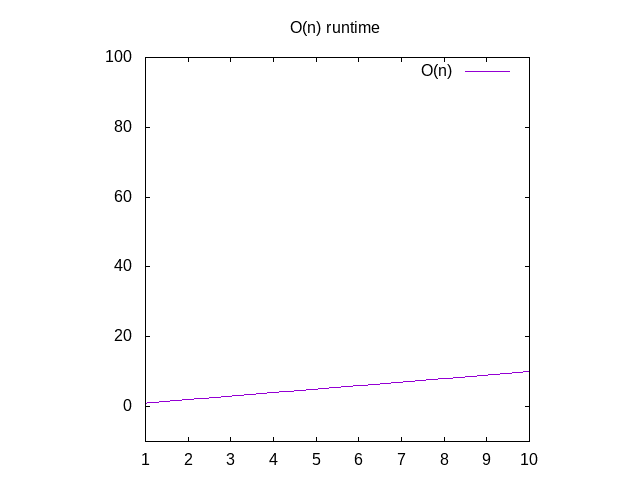
Figur 2: Runtime egenskaper hos en o(n) funktion
Så vad är några andra exempel på detta?
överväga denna funktion:
def is_none(item): return item is None
detta är lite av ett dumt exempel, men bär med mig. Denna funktion ärkallad O(1) som kallas”konstant tid”. Vad detta betyder är nomatter hur stor vår input är, det tar alltid samma tid att beräkna saker., Om du går tillbaka till Wolfram och plot 1 ser du att det alltid förblir detsamma, oavsett hur långt rätt vi går. Om youpass i en lista över 1 miljoner heltal, det tar ungefär samma tidsom om du skulle passera i en lista över 1 heltal. Konstant tid anses vara det bästa scenariot för en funktion.
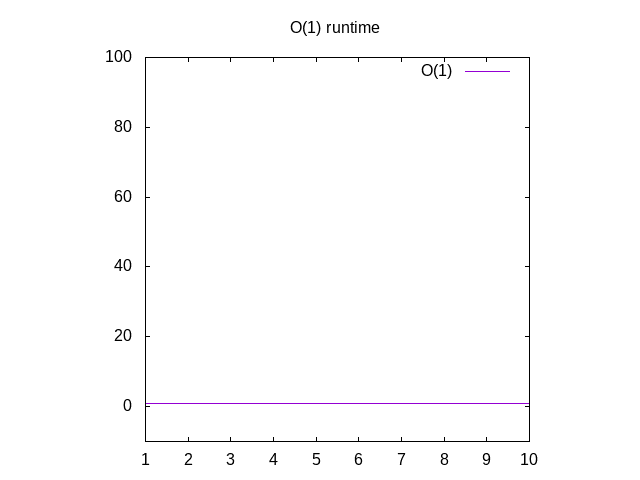
Figur 3: Runtime egenskaper för en o (1) funktion
överväga denna funktion:
nedan är en jämförelse av var och en av dessa grafer, som referens., Du kan se att en O(n^2) – funktion kommer att bli långsam mycket snabbt där som något som fungerar i konstant tid kommer att bli mycket bättre. Detta är särskilt användbart när det gäller datastrukturer, som jag kommer att lägga om snart.
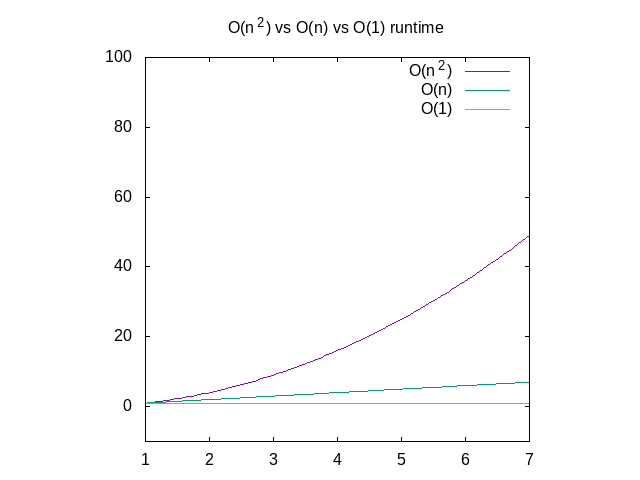
Figur 4: jämförelse av O(N2) vs o(n) vs o(1) funktioner
detta är en ganska hög nivå översikt över Big-O notation, men hoppfullygets du bekant med ämnet., Det finns en kurs somkan ge dig en mer djupgående uppfattning om detta ämne, men varnas för attdet kommer att hoppa in i matematisk notation mycket snabbt. Om något här inte vettigt, skicka mig ett mail.
uppdatering: Jag har också skrivit om hur man beräknar Big-O.
Jag funderar på att skriva en bok om detta ämne. Om det här är något du vill se, vänligen uttrycka ditt intresse för det här.