motstånd mot induktorer
induktorer beter sig inte på samma sätt som motstånd gör. Medan motstånd helt enkelt motsätter sig strömflödet genom dem (genom att släppa en spänning som är direkt proportionell mot strömmen), motsätter induktorer förändringar i ström genom dem, genom att släppa en spänning som är direkt proportionell mot strömändringshastigheten.
i enlighet med Lenz lag är denna inducerade spänning alltid av en sådan polaritet att man försöker behålla strömmen vid dess nuvarande värde., Det vill säga, om strömmen ökar i storlek, kommer den inducerade spänningen att ”trycka mot” strömflödet; om strömmen minskar kommer polariteten att vända och ”trycka med” strömmen för att motsätta sig minskningen.
detta motstånd mot nuvarande förändring kallas reaktans, snarare än motstånd., Uttryckt matematiskt är förhållandet mellan spänningen som sjönk över induktorn och hastigheten för strömförändring genom induktorn som sådan:

växelström i en enkel Induktiv krets
uttrycket di/dt är en från kalkyl, vilket betyder förändringstakten för momentan ström (i) över tiden, i ampere per sekund.
induktansen (L) är i Henrys, och den momentana spänningen (E) är naturligtvis i volt., Ibland hittar du hastigheten för momentan spänning uttryckt som ” v ”istället för” e ” (v = l di/dt), men det betyder exakt samma sak.
för att visa vad som händer med växelström, låt oss analysera en enkel induktor krets:
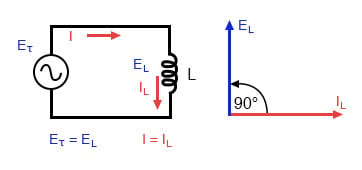
ren induktiv krets: induktor ström släpar induktor spänning med 90°.
om vi skulle rita strömmen och spänningen för denna mycket enkla krets skulle det se ut så här:

ren induktiv krets, vågformer.,
Kom ihåg att spänningen sjunkit över en induktor är en reaktion mot förändringen i ström genom den.
därför är den momentana spänningen noll när den momentana strömmen är högst (nollförändring eller nivåhöjning på den aktuella sinusvågen) och den momentana spänningen är högst varhelst den momentana strömmen är vid maximal förändring (punkterna med brantaste lutning på den aktuella vågen, där den korsar nolllinjen).
detta resulterar i en spänningsvåg som är 90° ur fas med den aktuella vågen., Om man tittar på grafen verkar spänningsvågen ha en ” huvudstart ”på den aktuella vågen; spänningen” leder ”strömmen och strömmen” släpar ” bakom spänningen.

ström släpar spänning med 90° i en ren induktiv krets.
saker blir ännu mer intressanta när vi plottar kraften för den här kretsen:

I en ren induktiv krets kan ögonblicklig effekt vara positiv eller negativ.,
eftersom momentan effekt är produkten av den momentana spänningen och den momentana strömmen (p=ie), är effekten lika med noll när den momentana strömmen eller spänningen är noll. När den momentana strömmen och spänningen är båda positiva (ovanför linjen) är effekten positiv.
som med resistorexemplet är effekten också positiv när den momentana strömmen och spänningen är båda negativa (under linjen).,
eftersom ström-och spänningsvågorna är 90° ur fas, finns det tillfällen då en är positiv medan den andra är negativ, vilket resulterar i lika frekventa förekomster av negativ momentan effekt.
Vad är negativ effekt?
men vad betyder negativ effekt? Det innebär att induktorn släpper ström tillbaka till kretsen, medan en positiv effekt innebär att den absorberar ström från kretsen.,
eftersom de positiva och negativa effektcyklerna är lika stora och varaktighet över tiden, släpper induktorn lika mycket ström tillbaka till kretsen som den absorberar över loppet av en komplett cykel.
vad detta innebär i praktisk mening är att reaktansen hos en induktor släpper ut nettoenergi av noll, helt till skillnad från motståndet hos ett motstånd, vilket släpper ut energi i form av värme. Märk väl, det här är bara för perfekta induktorer, som inte har något trådmotstånd.
reaktans vs., Motstånd
en induktors motstånd mot förändring i ström översätter till ett motstånd mot växelström i allmänhet, vilket per definition alltid förändras i ögonblicklig storlek och riktning.
detta motstånd mot växelström liknar motstånd men skiljer sig åt eftersom det alltid resulterar i en fasförskjutning mellan ström och spänning, och det släpper ut nollkraft. På grund av skillnaderna har den ett annat namn: reaktans. Reaktans till AC uttrycks i ohm, precis som motstånd är, förutom att dess matematiska symbol är X istället för R.,
för att vara specifik symboliseras reaktansen i samband med en induktor vanligen av bokstaven X med bokstaven L som ett subscript, så här: XL.
eftersom induktorer släpper spänningen i proportion till strömändringshastigheten, kommer de att släppa mer spänning för snabbare föränderliga strömmar och mindre spänning för långsammare föränderliga strömmar. Vad detta betyder är att reaktansen i ohm för någon induktor är direkt proportionell mot frekvensen av växelströmmen., Den exakta formeln för bestämning av reaktansen är följande:

om vi exponerar en 10 MH-induktor för frekvenser på 60, 120 och 2500 Hz kommer det att manifestera reaktanserna i tabellen nedan.
reaktans av en 10 MH induktor:
| frekvens (Hertz) | reaktans (Ohm) |
| 60 | 3.7699 |
| 120 | 7.5398 |
| 2500 | 157.,0796 |
i reaktansekvationen har termen ”2NF” (allt på höger sida utom l) en speciell betydelse för sig själv. Det är antalet radianer per sekund som växelströmmen ”roterar” på, om du föreställer dig en cykel av AC för att representera en full cirkels rotation.
en radian är en vinkelmätningsenhet: det finns 2π radianer i en hel cirkel, precis som det finns 360° i en hel cirkel., Om generatorn som producerar AC är en dubbelpolig enhet, kommer den att producera en cykel för varje full varv av axelrotation, vilket är varje 2π radianer, eller 360°.
om denna konstant på 2π multipliceras med frekvens i Hertz (cykler per sekund), blir resultatet en siffra i radianer per sekund, känd som AC-systemets vinkelhastighet.
vinkelhastighet i AC-system
vinkelhastighet kan representeras av uttrycket 2nf, eller det kan representeras av sin egen symbol, den gemena grekiska bokstaven omega, som liknar vår romerska gemena ”w”: ω., Således kan reaktansformeln XL = 2nfL också skrivas som XL = wL.
det måste förstås att denna ”vinkelhastighet” är ett uttryck för hur snabbt AC-vågformerna cyklar, en hel cykel som är lika med 2π radianer. Det är inte nödvändigtvis representativt för den faktiska axelhastigheten hos generatorn som producerar AC.
om generatorn har mer än två poler, kommer vinkelhastigheten att vara en multipel av axelhastigheten., Av denna anledning uttrycks ω ibland i enheter av elektriska radianer per sekund snarare än (vanligt) radianer per sekund, för att skilja det från mekanisk rörelse.
på något sätt uttrycker vi systemets vinkelhastighet, det är uppenbart att det är direkt proportionellt mot reaktansen i en induktor. Eftersom frekvensen (eller växelströmsaxelhastigheten) ökas i ett AC-system, kommer en induktor att erbjuda större motstånd mot strömpassagen och vice versa.,
växelström i en enkel induktiv krets är lika med spänningen (i volt) dividerat med den induktiva reaktansen (i ohm), precis som antingen växelström eller likström i en enkel resistiv krets är lika med spänningen (i volt) dividerat med motståndet (i ohm). En exempelkrets visas här:

Induktiv reaktans

Fasvinklar
Vi måste dock komma ihåg att spänning och ström inte befinner sig i fas här., Som visades tidigare har spänningen en fasförskjutning på + 90 ° med avseende på strömmen. Om vi representerar dessa fasvinklar av spänning och ström matematiskt i form av komplexa tal, finner vi att en induktors motstånd mot ström har en fasvinkel också:


ström släpar spänning med 90° i en induktor.
matematiskt säger vi att fasvinkeln för en induktors motstånd mot strömmen är 90°, vilket innebär att en induktors motstånd mot strömmen är en positiv imaginär mängd., Denna fasvinkel av reaktiv motstånd mot ström blir kritiskt viktig i kretsanalys, särskilt för komplexa AC-kretsar där reaktans och motstånd interagerar.
det kommer att visa sig fördelaktigt att representera någon komponents motstånd mot nuvarande när det gäller komplexa tal snarare än skalära mängder motstånd och reaktans.
recension:
- Induktiv reaktans är det motstånd som en induktor erbjuder till växelström på grund av dess fasförskjutna lagring och frisättning av energi i sitt magnetfält., Reaktansen symboliseras av bokstaven ” X ” och mäts i ohm precis som motstånd (R).
- Induktiv reaktans kan beräknas med hjälp av denna formel: XL = 2NFL
- vinkelhastigheten hos en AC-krets är ett annat sätt att uttrycka sin frekvens, i enheter av elektriska radianer per sekund istället för cykler per sekund. Det symboliseras av det små grekiska bokstaven ”omega” eller ω.
- Induktiv reaktans ökar med ökande frekvens. Med andra ord, ju högre frekvens desto mer motsätter sig växelströmsflödet av elektroner.,
relaterade kalkylblad:
- induktorer kalkylblad
- Induktiv reaktans kalkylblad