Support Vector Machine oder SVM ist einer der beliebtesten überwachten Lernalgorithmen, der sowohl für Klassifizierungs-als auch für Regressionsprobleme verwendet wird. Es wird jedoch hauptsächlich für Klassifizierungsprobleme im maschinellen Lernen verwendet.
Das Ziel des SVM-Algorithmus ist es, die beste Linie oder Entscheidungsgrenze zu erstellen, die den n-dimensionalen Raum in Klassen aufteilen kann, damit wir den neuen Datenpunkt in Zukunft problemlos in die richtige Kategorie einfügen können., Diese beste Entscheidungsgrenze wird Hyperplane genannt.
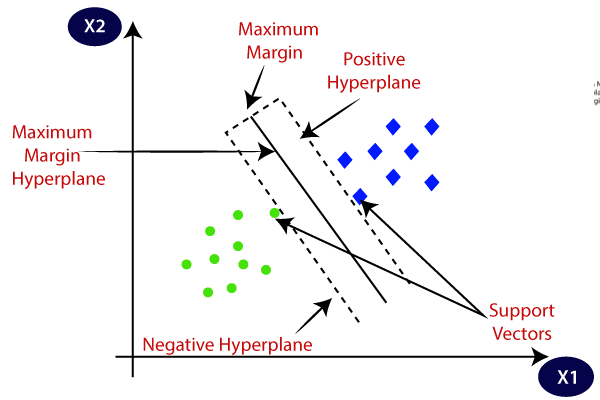
SVM wählt die Extrempunkte/Vektoren aus, die beim Erstellen der Hyperebene helfen. Diese extremen Fälle werden als Unterstützungsvektoren bezeichnet, und daher wird Algorithmus als Unterstützungsvektormaschine bezeichnet. Betrachten Sie das folgende Diagramm, in dem zwei verschiedene Kategorien mithilfe einer Entscheidungsgrenze oder einer Hyperebene klassifiziert werden:
Beispiel: SVM kann mit dem Beispiel verstanden werden, das wir im KNN-Klassifikator verwendet haben., Angenommen, wir sehen eine seltsame Katze, die auch einige Merkmale von Hunden hat, wenn wir also ein Modell wollen, das genau identifizieren kann, ob es sich um eine Katze oder einen Hund handelt, kann ein solches Modell mithilfe des SVM-Algorithmus erstellt werden. Wir werden zuerst unser Modell mit vielen Bildern von Katzen und Hunden trainieren, damit es über verschiedene Merkmale von Katzen und Hunden lernen kann, und dann testen wir es mit dieser seltsamen Kreatur. Wenn der Unterstützungsvektor eine Entscheidungsgrenze zwischen diesen beiden Daten (Katze und Hund) erstellt und Extremfälle (Unterstützungsvektoren) auswählt, wird der Extremfall von Katze und Hund angezeigt., Auf der Grundlage der Stützvektoren wird es als Katze klassifiziert. Betrachten Sie das folgende Diagramm:
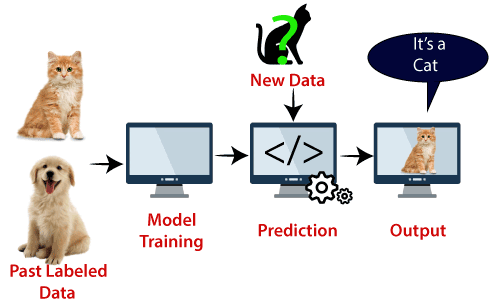
Der SVM-Algorithmus kann für Gesichtserkennung, Bildklassifizierung, Textkategorisierung usw. verwendet werden.
SVM-Typen
SVM kann von zwei Typen sein:
- Linear SVM: Linear SVM wird für linear trennbare Daten verwendet, dh wenn ein Datensatz mithilfe einer einzelnen geraden Linie in zwei Klassen eingeteilt werden kann, werden solche Daten als linear trennbare Daten bezeichnet, und der Klassifikator wird als linearer SVM-Klassifikator bezeichnet.,
- Nichtlineares SVM: Nichtlineares SVM wird für nicht linear getrennte Daten verwendet, dh wenn ein Datensatz nicht mithilfe einer geraden Linie klassifiziert werden kann, werden diese Daten als nichtlineare Daten bezeichnet und Klassifikator verwendet wird als nichtlinearer SVM-Klassifikator bezeichnet.
Hyperplane und Unterstützungsvektoren im SVM-Algorithmus:
Hyperplane: Es kann mehrere Zeilen / Entscheidungsgrenzen geben, um die Klassen im n-dimensionalen Raum zu trennen, aber wir müssen die beste Entscheidungsgrenze herausfinden, die hilft, die Datenpunkte zu klassifizieren. Diese beste Grenze ist als Hyperplane von SVM bekannt.,
Die Abmessungen der Hyperebene hängen von den im Datensatz vorhandenen Merkmalen ab, dh wenn zwei Merkmale vorhanden sind (wie im Bild gezeigt), ist die Hyperebene eine gerade Linie. Und wenn es 3 Funktionen gibt, dann wird Hyperplane eine 2-dimensionale Ebene sein.
Wir erstellen immer eine Hyperebene mit einem maximalen Abstand, dh dem maximalen Abstand zwischen den Datenpunkten.
Unterstützungsvektoren:
Die Datenpunkte oder Vektoren, die der Hyperebene am nächsten sind und die Position der Hyperebene beeinflussen, werden als Unterstützungsvektor bezeichnet., Da diese Vektoren die Hyperebene unterstützen, wird sie als Unterstützungsvektor bezeichnet.
Wie funktioniert SVM?
Linear SVM:
Die Funktionsweise des SVM-Algorithmus kann anhand eines Beispiels verstanden werden. Angenommen, wir haben ein Dataset mit zwei Tags (grün und blau) und das Dataset hat zwei Features x1 und x2. Wir möchten einen Klassifikator, der das Koordinatenpaar(x1, x2) entweder grün oder blau klassifizieren kann. Betrachten Sie das folgende Bild:
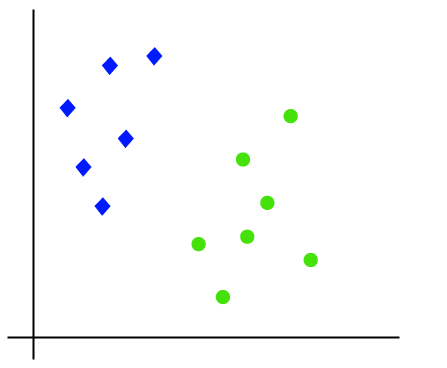
Da es sich also um einen 2D-Raum handelt, können wir diese beiden Klassen einfach trennen, indem wir nur eine gerade Linie verwenden., Es können jedoch mehrere Zeilen vorhanden sein, die diese Klassen trennen können. Betrachten Sie das folgende Bild:
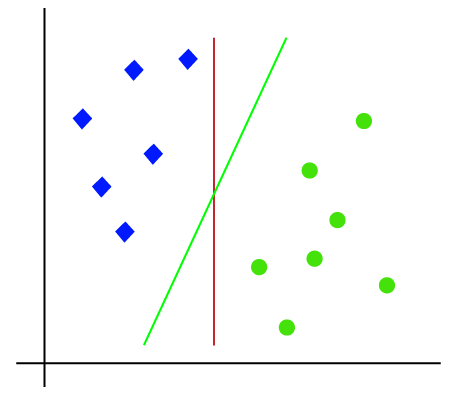
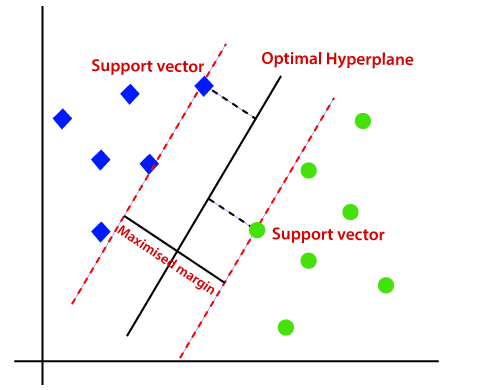
Daher hilft der SVM-Algorithmus, die beste Linien-oder Entscheidungsgrenze zu finden; Diese beste Grenze oder Region wird als Hyperebene bezeichnet. SVM-Algorithmus findet den nächsten Punkt der Linien aus beiden Klassen. Diese Punkte werden als Stützvektoren bezeichnet. Der Abstand zwischen den Vektoren und der Hyperebene wird als Marge bezeichnet. Und das Ziel des SVM ist es, diese Marge zu maximieren. Die Hyperebene mit maximaler Marge wird als optimale Hyperebene bezeichnet.,
Nichtlineares SVM:
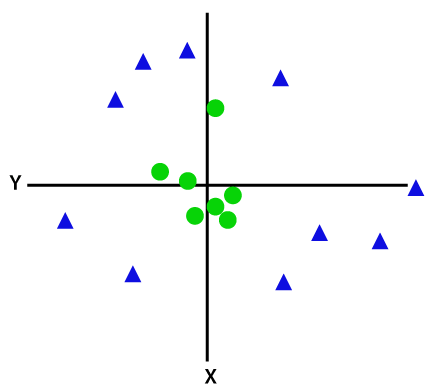
Wenn Daten linear angeordnet sind, können wir sie mithilfe einer geraden Linie trennen, aber für nichtlineare Daten können wir keine einzige gerade Linie zeichnen. Betrachten Sie das folgende Bild:
Um diese Datenpunkte zu trennen, müssen wir eine weitere Dimension hinzufügen. Für lineare Daten haben wir zwei Dimensionen x und y verwendet, daher fügen wir für nichtlineare Daten eine dritte Dimension z hinzu., Es kann berechnet werden als:
z=x2 +y2
Durch Hinzufügen der dritten Dimension wird der Beispielraum wie folgt dargestellt:
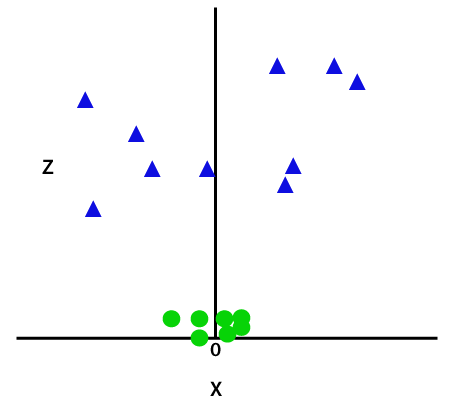
Jetzt teilt SVM die Datensätze auf folgende Weise in Klassen auf. Betrachten Sie das folgende Bild:
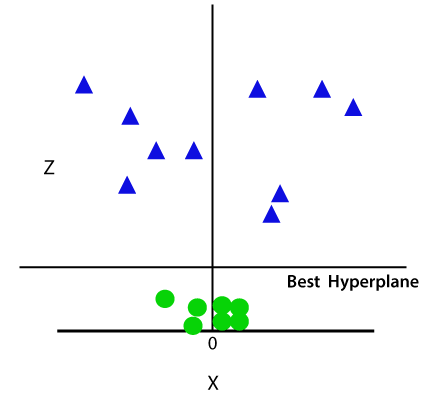
Da wir uns im 3D-Raum befinden, sieht es wie eine Ebene parallel zur x-Achse aus. Wenn wir es in den 2D-Raum mit z=1 konvertieren, wird es wie folgt aussehen:
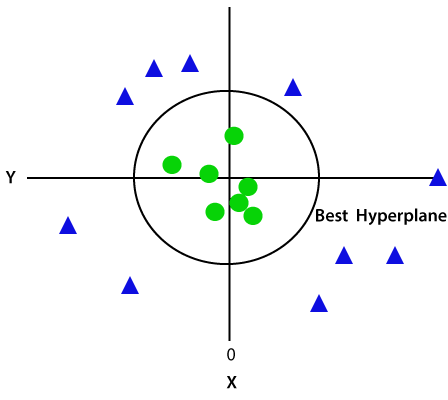
Daher erhalten wir bei nichtlinearen Daten einen Umfang von Radius 1.,
Python-Implementierung von Support Vector Machine
Jetzt implementieren wir den SVM-Algorithmus mit Python. Hier verwenden wir denselben Datensatz user_data, den wir in der logistischen Regression und KNN-Klassifizierung verwendet haben.
- Datenvorverarbeitungsschritt
Bis zum Datenvorverarbeitungsschritt bleibt der Code derselbe. Unten ist der Code:
Nach der Ausführung des obigen Codes werden wir die Daten vorverarbeiten., Der Code gibt den Datensatz wie folgt an:
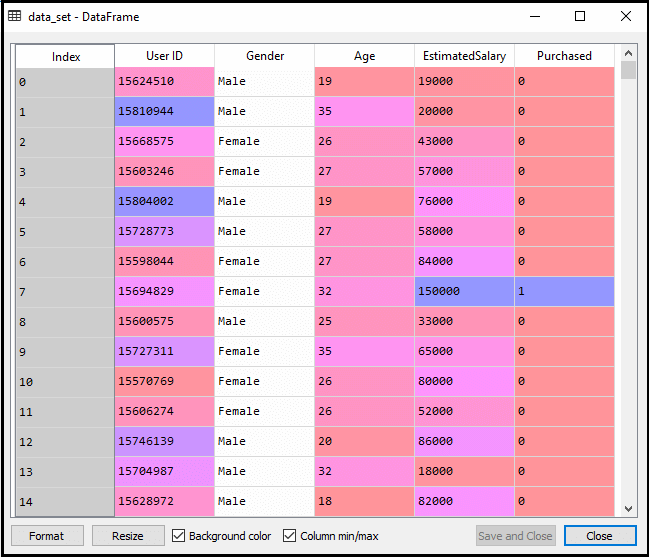
Die skalierte Ausgabe für den Testsatz lautet:
Anpassung des SVM-Klassifikators an den Trainingssatz:
Jetzt wird der Trainingssatz an den SVM-Klassifikator angepasst. Um den SVM-Klassifikator zu erstellen, importieren wir die SVC-Klasse aus Sklearn.svm-Bibliothek. Unten ist der Code dafür:
Im obigen Code haben wir kernel=’linear‘, da wir hier SVM für linear trennbare Daten erstellen. Wir können es jedoch für nichtlineare Daten ändern., Und dann haben wir den Klassifikator an den Trainingsdatensatz(x_train, y_train)
Ausgabe angepasst:
Die Modellleistung kann durch Ändern des Werts von C(Regularisierungsfaktor), Gamma und Kernel geändert werden.
- Vorhersage des Testsatzes Ergebnis:
Nun werden wir die Ausgabe für Testsatz vorherzusagen. Dazu erstellen wir einen neuen Vektor y_pred. Unten ist der Code dafür:
Nachdem wir den y_pred-Vektor erhalten haben, können wir das Ergebnis von y_pred und y_test vergleichen, um den Unterschied zwischen dem tatsächlichen Wert und dem vorhergesagten Wert zu überprüfen.,
Ausgabe: Unten ist die Ausgabe für die Vorhersage des Testsatzes:

- Erstellen der Verwirrungsmatrix:
Jetzt sehen wir die Leistung des SVM-Klassifikators, wie viele falsche Vorhersagen im Vergleich zum logistischen Regressionsklassifikator vorhanden sind. Um die Verwirrungsmatrix zu erstellen, müssen wir die Funktion confusion_matrix der sklearn-Bibliothek importieren. Nach dem Import der Funktion rufen wir sie mit einer neuen Variablen cm auf. Die Funktion verwendet zwei Parameter, hauptsächlich y_true (die tatsächlichen Werte) und y_pred (der vom Klassifikator angegebene Wert)., Unten ist der Code dafür:
Ausgabe:
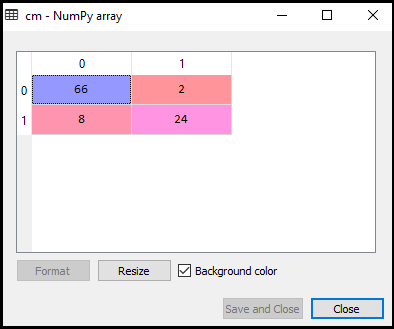
Wie wir im obigen Ausgabebild sehen können, gibt es 66+24= 90 korrekte Vorhersagen und 8+2= 10 korrekte Vorhersagen. Daher können wir sagen, dass sich unser SVM-Modell im Vergleich zum logistischen Regressionsmodell verbessert hat.,
- Visualisierung des Trainingssatzergebnisses:
Jetzt werden wir das Trainingssatzergebnis visualisieren, unten ist der Code dafür:
Ausgabe:
Durch Ausführen des obigen Codes erhalten wir die Ausgabe als:
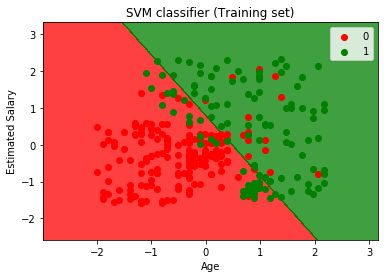
Wie wir sehen können, erscheint die obige Ausgabe ähnlich der logistischen Regressionsausgabe. In der Ausgabe haben wir die gerade Linie als Hyperebene erhalten, da wir im Klassifikator einen linearen Kernel verwendet haben. Und wir haben auch oben besprochen, dass für den 2D-Raum die Hyperebene in SVM eine gerade Linie ist.,
- Visualisierung des Testsatzes Ergebnis:
Ausgabe:
Durch Ausführen des obigen Codes erhalten wir die Ausgabe als:
Wie wir im obigen Ausgabebild sehen können, hat der SVM-Klassifikator die Benutzer in zwei Regionen unterteilt (gekauft oder nicht gekauft). Benutzer, die das SUV gekauft haben, befinden sich im roten Bereich mit den roten Streupunkten. Und Benutzer, die das SUV nicht gekauft haben, befinden sich in der grünen Region mit grünen Streupunkten. Die Hyperplane hat die beiden Klassen in gekaufte und nicht gekaufte Variable unterteilt.