resultados de aprendizagem
- Identificar os focos, vértices, eixos e centro de uma elipse.
- escrever equações de elipses centradas na origem.
- escrever equações de elipses não centradas na origem.
uma secção cónica, ou cónica, é uma forma resultante da intersecção de um cone circular direito com um plano. O ângulo em que o plano intersecta o cone determina a forma.,
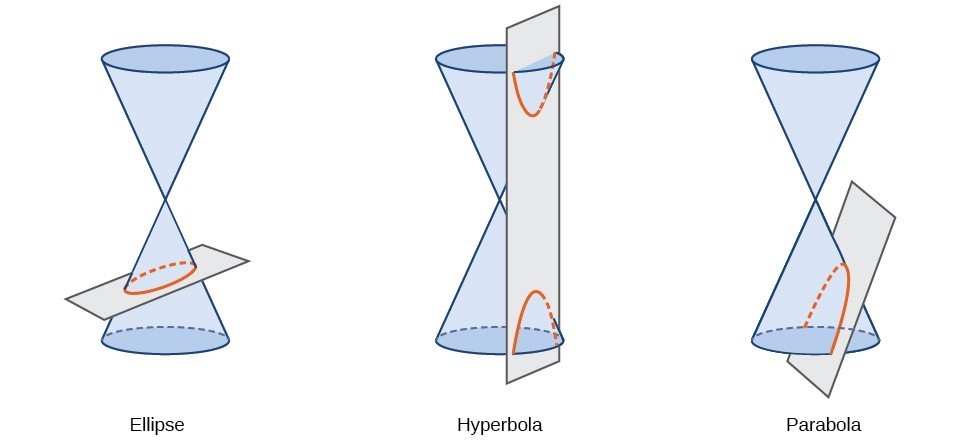
Conic sections can also be described by a set of points in the coordinate plane. Mais tarde neste capítulo veremos que o grafo de qualquer equação quadrática em duas variáveis é uma seção Cónica. Os sinais das equações e os coeficientes dos Termos variáveis determinam a forma. Esta seção foca nas quatro variações da forma padrão da equação para a elipse. Uma elipse é o conjunto de todos os pontos \esquerda (x, y\direita) em um plano tal que a soma de suas distâncias de dois pontos fixos é uma constante., Cada ponto fixo é chamado de foco (plural: foci) da elipse.
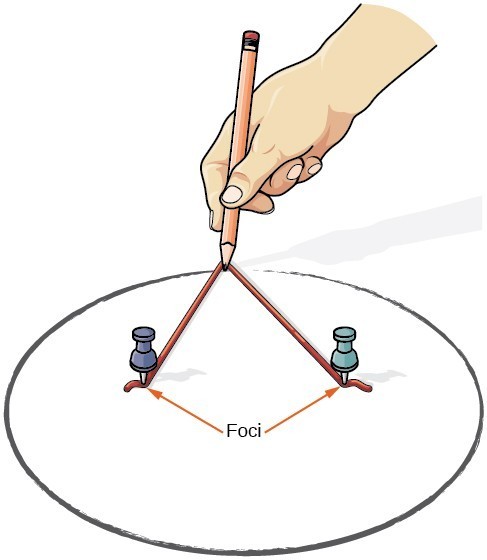
podemos desenhar uma elipse usando um pedaço de papelão, duas miniaturas, um lápis e uma corda. Colocar as miniaturas no cartão para formar o focinho da elipse. Cortar um pedaço de cadeia mais longo do que a distância entre as duas miniaturas (o comprimento da cadeia representa a constante na definição). Amarre cada extremidade da corda ao papelão, e trace uma curva com um lápis esticado contra a corda. O resultado é uma elipse.
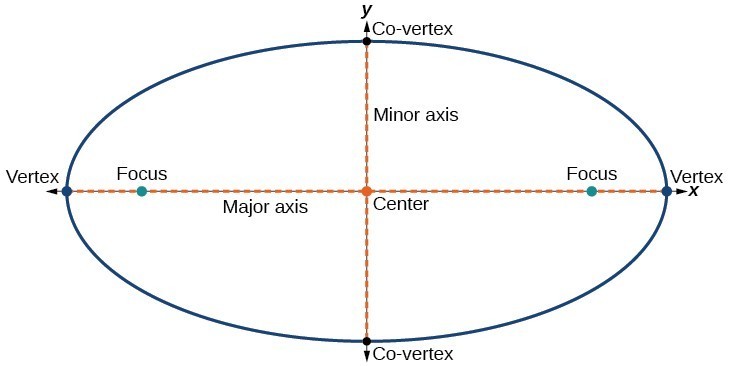
cada elipse tem dois eixos de simetria., O eixo maior é chamado de eixo maior, e o eixo menor é chamado de eixo menor. Cada ponto final do eixo principal é o vértice da elipse (plural: vértices), e cada ponto final do eixo menor é um co-vértice da elipse. O centro de uma elipse é o ponto médio dos eixos maior e menor. Os eixos são perpendiculares ao centro. O focinho sempre se encontra no eixo principal, e a soma das distâncias do focinho para qualquer ponto da elipse (a soma constante) é maior do que a distância entre os focos.,
nesta secção restringimos elipses àqueles que são posicionados verticalmente ou horizontalmente no plano de coordenadas. Ou seja, os eixos podem ficar ou ser paralelos aos eixos x– e y -. Mais tarde, no capítulo, veremos elipses que são rodadas no plano de coordenadas.para trabalhar com elipses horizontais e verticais no plano de coordenadas, consideramos dois casos: aqueles que estão centrados na origem e aqueles que estão centrados em um ponto diferente da origem., Primeiro vamos aprender a derivar as equações de elipses, e então vamos aprender a escrever as equações de elipses em forma padrão. Mais tarde vamos usar o que aprendemos para desenhar os gráficos.,v>Se (x,y) é um ponto da elipse, em seguida, podemos definir as seguintes variáveis:
\begin{align}d_1&=\text{a distância do } (-c,0) \text{ a } (x,y) \\ d_2&= \text{a distância do } (c,0) \text{ a } (x,y) \end{align}
\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1
para uma elipse centrada na origem, com o seu eixo maior sobre o eixo X e
\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1
para uma elipse centrada na origem, com o seu eixo maior sobre o eixo-Y.,
Escrever as Equações das Elipses Não Centrado na Origem
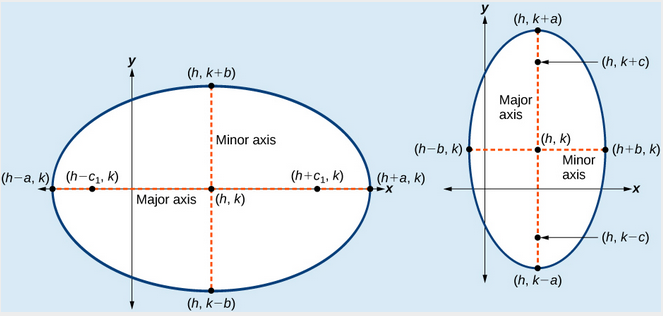
(a) Horizontal elipse com centro \left(h,k\right) (b) Vertical elipse com centro \left(h,k\right)
de problemas Aplicados a Problemas Envolvendo Elipses
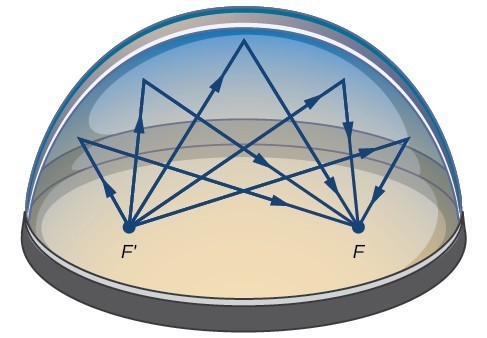
Muitas situações do mundo real podem ser representados por elipses, incluindo órbitas dos planetas, satélites, luas e cometas, e formas de barco de quilha, lemes, e alguns com asas de avião. Um dispositivo médico chamado litotripter usa Refletores elípticos para quebrar pedras renais gerando ondas sonoras., Alguns edifícios, chamados câmaras sussurrantes, são projetados com cúpulas elípticas de modo que uma pessoa sussurrando em um foco pode facilmente ser ouvida por alguém de pé no outro foco. Isto ocorre por causa das propriedades acústicas de uma elipse. Quando uma onda sonora se origina em um foco de uma câmara sussurrante, a onda sonora será refletida fora da cúpula elíptica e de volta para o outro foco. Na Câmara dos sussurros do Museu de Ciência e indústria em Chicago, duas pessoas de pé no focus—cerca de 43 pés de distância—podem ouvir-se sussurrar.