Support Vector Machine or SVM is one of the most popular Supervised Learning algorithms, which is used for Classification as well as Regression problems. No entanto, principalmente, é usado para problemas de classificação na aprendizagem de máquinas.
O objetivo do algoritmo SVM é criar a melhor linha ou limite de decisão que pode segregar espaço n-dimensional em classes, de modo que podemos facilmente colocar o novo ponto de dados na categoria correta no futuro., Esta melhor fronteira de decisão é chamada de hiperplano.
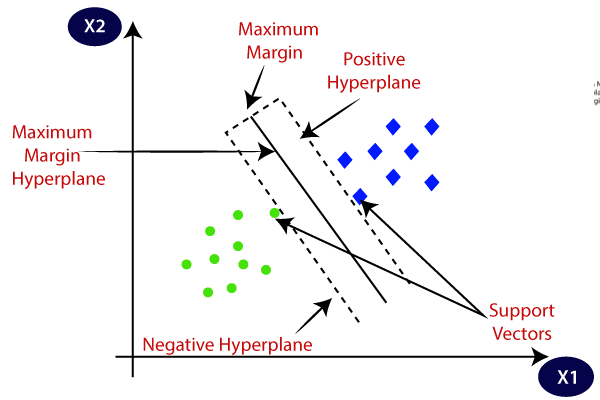
SVM escolhe os pontos extremos/vetores que ajudam na criação do hiperplano. Estes casos extremos são chamados como vetores de suporte, e, portanto, algoritmo é chamado como máquina de suporte vetorial. Considere o diagrama abaixo no qual existem duas categorias diferentes que são classificadas usando um limite de decisão ou hiperplano:
exemplo: SVM pode ser entendido com o exemplo que temos usado no classificador KNN., Suponha que vemos um gato estranho que também tem algumas características de cães, então se queremos um modelo que pode identificar com precisão se é um gato ou cão, então tal modelo pode ser criado usando o algoritmo SVM. Vamos primeiro treinar o nosso modelo com muitas imagens de gatos e cães para que ele possa aprender sobre diferentes características de gatos e cães, e então nós testá-lo com esta estranha criatura. Assim como o vetor de suporte cria uma fronteira de decisão entre estes dois dados (gato e cão) e escolher casos extremos (vetores de suporte), ele vai ver o caso extremo de gato e cão., Com base nos vectores de suporte, classificá-lo-á como um gato. Considere o diagrama abaixo:
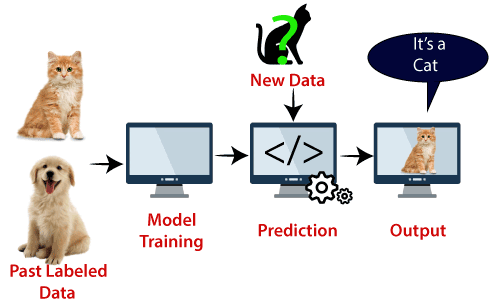
SVM algorithm can be used for Face detection, image classification, text categorization, etc.
Tipos de SVM
SVM pode ser de dois tipos:
- SVM Linear: SVM Linear é utilizado para linearmente separáveis de dados, o que significa que se um conjunto de dados podem ser classificados em duas classes, utilizando uma única linha reta, em seguida, tais dados é denominado como linearmente separáveis de dados, e classificador é utilizado chamado de Linear, classificador SVM.,
- SVM não-linear: SVM não-Linear é usado para dados não-linearmente separados, o que significa que se um conjunto de dados não pode ser classificado usando uma linha reta, então tais dados são denominados como dados não-lineares e classificador usado é chamado como classificador SVM não-linear.
Hiperplano de Suporte e Vetores no algoritmo SVM:
Hiperplano: pode haver várias linhas/decisão limites para segregar as classes no espaço n-dimensional, mas nós precisamos descobrir a melhor decisão fronteira que ajuda a classificar os pontos de dados. Este melhor limite é conhecido como o hiperplano da SVM.,
As dimensões do hiperplano dependem das características presentes no conjunto de dados, o que significa que se existem 2 características (como mostrado na imagem), então hyperplane será uma linha reta. E se houver 3 características, então hyperplane será um plano de 2 dimensões.
sempre criamos um hiperplano que tem uma margem máxima, o que significa a distância máxima entre os pontos de dados.
Suporte de Vetores:
Os pontos de dados ou vetores que são os mais próximos do hiperplano e que afetam a posição do hiperplano são chamados de Vetor de Suporte., Uma vez que estes vetores suportam o hiperplano, portanto chamado de vetor de suporte.como funciona a SVM?
SVM Linear:
o trabalho do algoritmo SVM pode ser entendido usando um exemplo. Suponha que temos um conjunto de dados que tem duas tags (verde e azul), e o conjunto de dados tem duas características x1 e x2. Queremos um classificador que possa classificar o par (x1, x2) de coordenadas em verde ou azul. Considere a imagem abaixo:
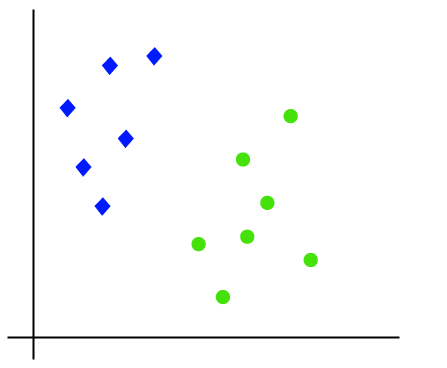
de modo que é espaço 2-d assim, usando apenas uma linha reta, podemos facilmente separar estas duas classes., Mas pode haver várias linhas que podem separar essas classes. Considere a imagem abaixo:
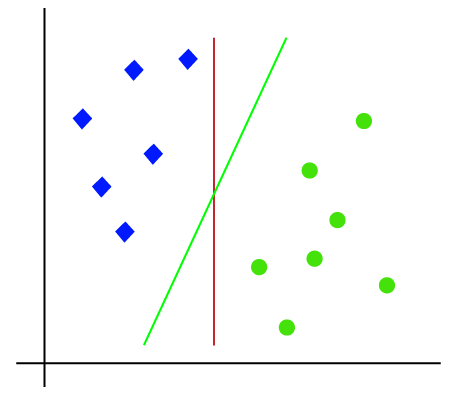
portanto, o algoritmo SVM ajuda a encontrar a melhor linha ou limite de decisão; este melhor limite ou região é chamado como um hiperplano. SVM algorithm finds the closest point of the lines from both the classes. Estes pontos são chamados vetores de suporte. A distância entre os vetores e o hiperplano é chamada de margem. E o objetivo da SVM é maximizar essa margem. O hiperplano com margem máxima é chamado de hiperplano ideal.,
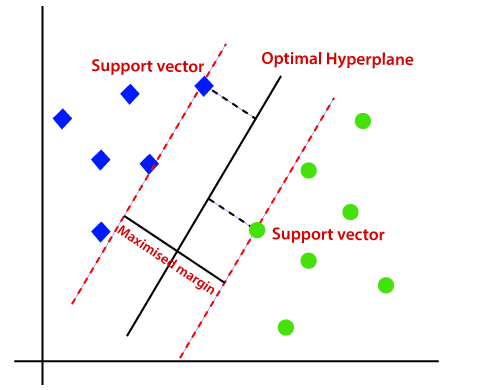
Não-Linear SVM:
Se os dados são linearmente organizado, então podemos separá-lo usando uma linha reta, mas para os não-linear de dados, podemos desenhar uma única linha reta. Considere a imagem abaixo:
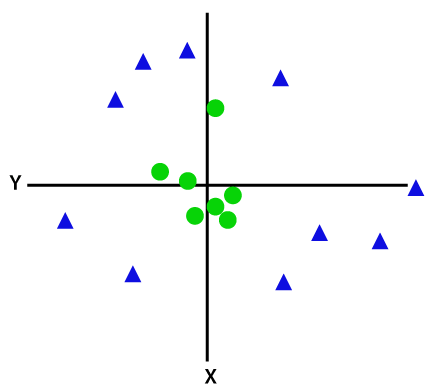
de modo a separar estes pontos de dados, precisamos adicionar mais uma dimensão. Para dados lineares, temos usado duas dimensões x e y, então para dados não lineares, vamos adicionar uma terceira dimensão Z., Ele pode ser calculado como:
z=x2 +y2
adicionando a terceira dimensão, a exemplo de espaço ficará como a imagem abaixo:
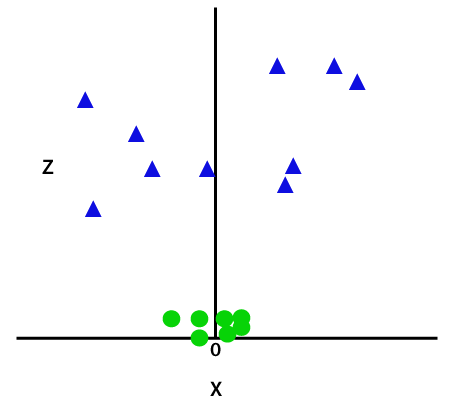
agora, o SVM vai dividir o conjunto de dados em classes, da seguinte forma. Considere a imagem abaixo:
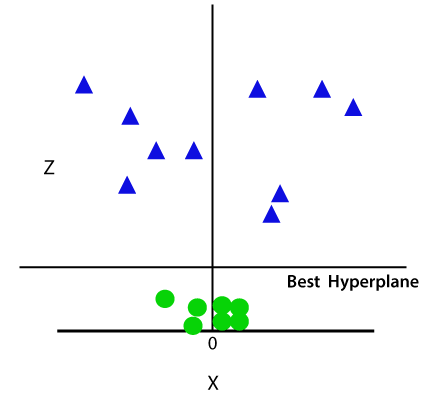
Uma vez que estamos em espaço 3-d, portanto, ele está parecendo um plano paralelo ao eixo x. Se nós convertê-lo em espaço 2d com z=1, então ele se tornará como:
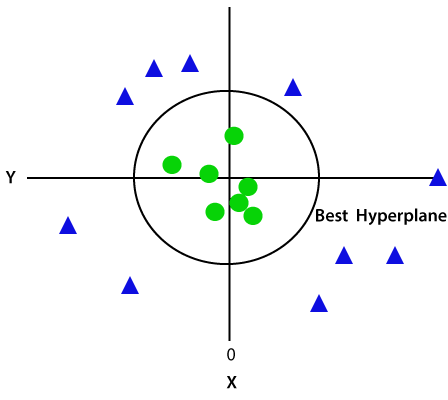
daí nós obtemos uma circunferência de raio 1 no caso de dados não-lineares.,
Python Implementation of Support Vector Machine
Now we will implement the SVM algorithm using Python. Aqui vamos usar o mesmo dataset user_data, que usamos na regressão logística e classificação KNN.
- fase de pré-processamento de dados
até à fase de pré-processamento de dados, o código permanecerá o mesmo. Abaixo está o código:
Depois de executar o código acima, vamos pré-processar os dados., O código vai dar o conjunto de dados como:
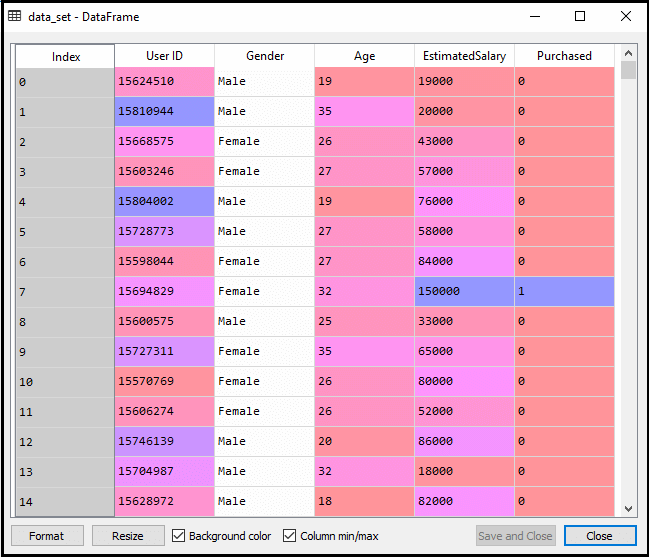
A saída ajustada para o conjunto de teste será:
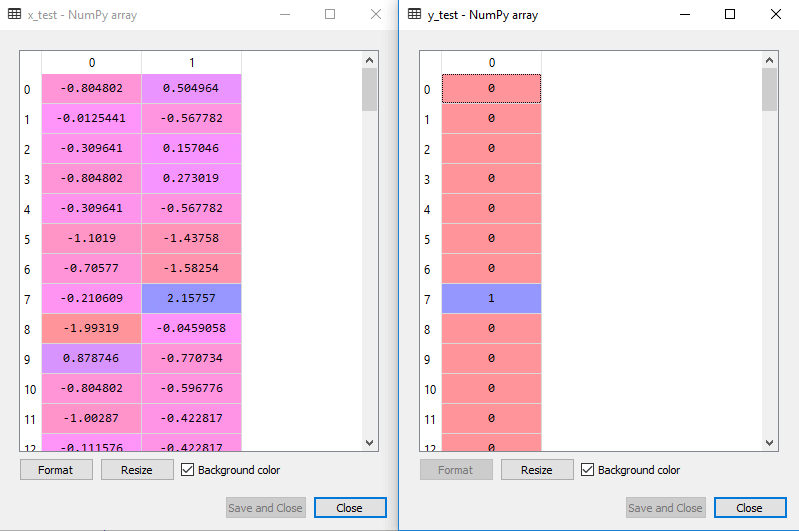
a Montagem da classificador SVM para o conjunto de treinamento:
Agora, o conjunto de treinamento que será montado para o classificador SVM. Para criar o classificador SVM, vamos importar a classe SVC do Sklearn.biblioteca svm. Abaixo está o código para ele:
no código acima, temos usado kernel=’linear’, como aqui estamos criando SVM para dados separáveis linearmente. No entanto, podemos alterá-lo para dados não lineares., E, em seguida, foi instalado o classificador para o conjunto de dados de treinamento(x_train, y_train)
Saída:
O desempenho do modelo pode ser alterada alterando o valor de C(fator de Regularização), de gama e de kernel.
- Predicting the test set result:
Now, we will predict the output for test set. Para isso, vamos criar um novo vetor y_pred. Abaixo está o código:
Depois de receber o y_pred vetor, podemos comparar o resultado de y_pred e y_test para verificar a diferença entre o valor real e o valor previsto.,
Saída: Abaixo está a saída para a predição de que o conjunto de teste:

- Criar a matriz de confusão:
Agora vamos ver o desempenho do classificador SVM que como muitas previsões incorretas há comparado à de regressão Logística classificador. Para criar a matriz de confusão, precisamos importar a função confusion_matrix da biblioteca sklearn. Depois de importar a função, vamos chamá-la usando uma nova variável cm. A função toma dois parâmetros, principalmente y_true (os valores reais) e y_pred (o valor alvo retornado pelo classificador)., Abaixo está o código:
Saída:
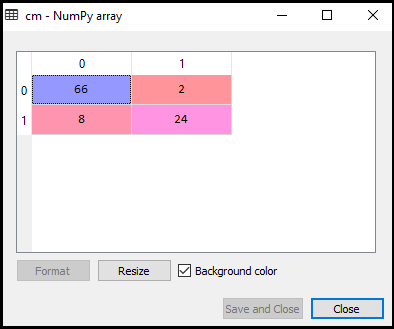
Como podemos ver acima, a imagem de saída, há 66+24= 90 previsões corretas e 8+2= 10 previsões corretas. Portanto, podemos dizer que nosso modelo SVM melhorou em comparação com o modelo de regressão logística.,
- Visualização do conjunto de treinamento resultado:
Agora vamos visualizar o conjunto de treinamento resultado, abaixo está o código:
Saída:
Ao executar o código acima, vamos obter o resultado como:
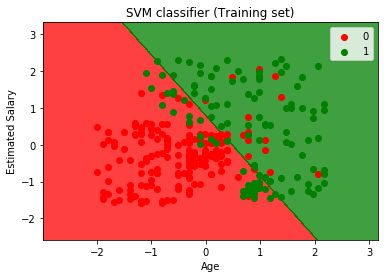
Como podemos ver, a saída acima está aparecendo semelhante à regressão Logística de saída. Na saída, nós temos a linha reta como hyperplane porque nós usamos um kernel linear no classificador. E nós também discutimos acima que para o espaço 2d, o hiperplano em SVM é uma linha reta.,
- Visualizando o conjunto de teste resultado:
Saída:
Ao executar o código acima, vamos obter o resultado como:
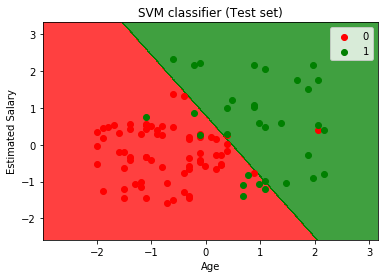
Como podemos ver acima, a imagem de saída, o classificador SVM divide os usuários em duas regiões (Adquiridos ou Não adquiridos). Os usuários que compraram o SUV estão na região vermelha com os pontos de dispersão vermelho. E os usuários que não compraram o SUV estão na região verde com pontos de dispersão verde. O hiperplano dividiu as duas classes em Variável comprada e não comprada.