esta é a primeira de uma série de três posts. O segundo post fala sobre como calcular Big-O. O terceiro artigo fala sobre a compreensão da definição formal de notação Big-O. Pensei que era assim que os programadores “reais” falavam do seu código. Foi tudo mais assustador porque as descrições acadêmicas (como a Wikipédia) fizeram muito pouco sentido para mim. Isto é frustrante porque os conceitos subjacentes não são assim tão difíceis.,
simply put, Big-O notation is how programmers talk aboutalgorithms. Algoritmos são outro tópico assustador que eu vou cobrir em outro post, mas para os nossos propósitos, vamos dizer que “algoritmo” significa uma função em seu programa (que não está muito longe). A big-Onotation de uma função é determinada pela forma como ela responde a diferentes entradas. Quão mais lento é se lhe dermos uma lista de 1000 coisas para trabalhar em vez de uma lista de 1 coisa?
considere este código:
def item_in_list(to_check, the_list): for item in the_list: if to_check == item: return True return False
portanto, se chamarmos esta função como item_in_list(2, ), deve ser muito rápido., Analisamos cada coisa na lista e se encontrarmos o primeiro argumento para a nossa função, retornaremos verdadeiro. Se chegarmos ao fim e não o encontrarmos, devolve falso.
a “complexidade” desta função é O(n). Vou explicar o que isto significa em apenas um segundo, mas vamos acabar com este problema matemático. O(n) é lido “ordem de N” porque a função O é também conhecida como a função ordem. Eu acho que isso é porque estamos fazendo uma aproximação, que lida em “ordens de magnitude”.,
“ordens de magnitude” é ainda outro termo matemático que, basicamente, diz a diferença entre classes de números. Pense na diferença entre 10 e 100. Se imaginares 10 dos teus amigos mais próximos e 100 pessoas, é uma grande diferença. Da mesma forma, a diferença entre 1.000 e 10.000 é bastante grande (na verdade, é a diferença entre um carro junker e um levemente usado). Acontece que, por aproximação,desde que esteja dentro de uma ordem de grandeza, está muito perto., Se adivinhasse o número de bolas de amachine, estaria dentro de uma ordem de grandeza se dissesse 200 bolas. 10 mil bolas de gumballs seriam muito diferentes.

Figura 1: Uma máquina de chicletes cujo número de chicletes é, provavelmente, dentro de uma ordem de magnitude de 200.
de Volta para dissecar O(n), este diz que, se fôssemos gráfico a timeit leva para executar esta função com diferentes tamanhos de entradas (e.g. anarray de 1 item, 2 itens, 3 itens, etc), veríamos que itapproximately corresponde ao número de itens na matriz., Isto é chamado de grafo linear. Isto significa que a linha é basicamente reta se você estava para grafá-la.
alguns de vocês podem ter percebido que se, na amostra de código acima, ouritem foi sempre o primeiro item da lista, o nosso código seria realyfast! Isso é verdade,mas Big-O é tudo sobre o pior desempenho aproximado de fazer algo. O pior caso para o código acima é que aquilo que procuramos não está na lista. (Note:The math term for this is “upper bound”, which means its talking about the mathematic limit of awfulness).,
Se você queria ver um gráfico para estas funções, você ignorar o O()função e alterar a variável n para x. Pode então escrever isso em Wolfram Alpha como “plot x”, que lhe mostrará uma diagonal. A razão pela qual você troca n Por x é que seus programas de graficação wants x como seu nome variável porque ele corresponde ao xaxis. O eixo-x a ficar maior da esquerda para a direita corresponde a alternar matrizes cada vez maiores para a sua função., O Y-axis representa o tempo, então quanto maior a linha, mais lento é.
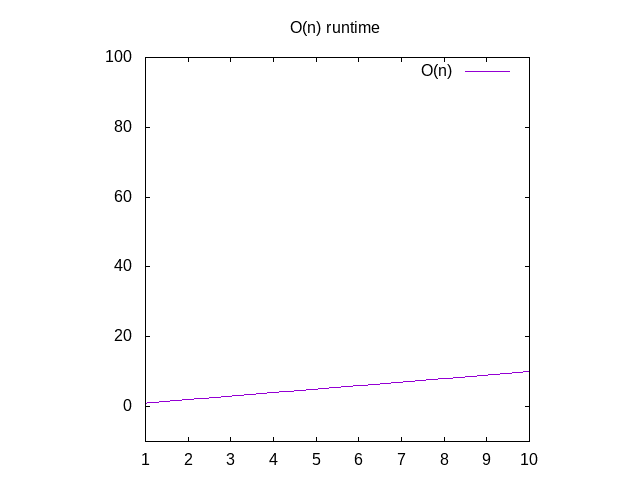
Figura 2: características de tempo de execução O(n) a função
Então, quais são alguns outros exemplos?
considere esta função:
def is_none(item): return item is None
Este é um pouco de um exemplo tolo, mas tenha paciência comigo. Esta função é chamada O(1) que é chamada de “tempo constante”. O que isto significa é que não importa quão grande é a nossa entrada, é sempre preciso a mesma quantidade de tempo para computar as coisas., Se você voltar para Wolfram e plot 1, você vai ver que ele sempre permanece o mesmo, não importa quão longe nós vamos para a direita. Se você aparecer em uma lista de 1 milhão de inteiros, vai demorar mais ou menos o mesmo tempo se você fosse passar em uma lista de 1 inteiro. O tempo constante é considerado o melhor cenário para uma função.
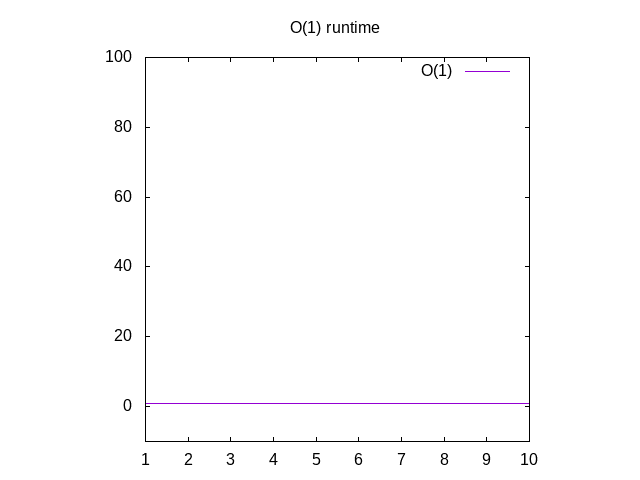
Figura 3: características de tempo de execução de uma(1) função
Considerar esta função:
Abaixo está uma comparação de cada um destes gráficos, para referência., Você pode ver que uma função O(n^2) vai ficar lenta muito rapidamente, onde como algo que opera em tempo constante será muito melhor. Isto é particularmente útil quando se trata de estruturas de dados, que eu vou postar em breve.
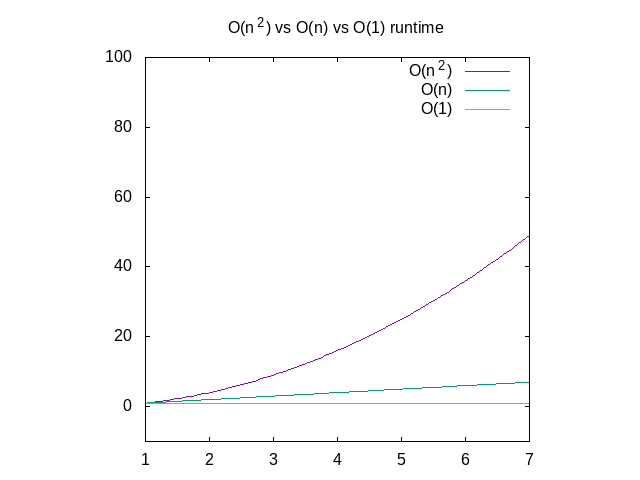
Figura 4: comparação de o(n2) vs o(n) vs o(1) funções
esta é uma visão de alto nível da notação Big-O, mas espero que conheça o tópico., Há um curso de coursera que pode dar-lhe uma visão mais aprofundada sobre este tópico, mas seja avisado que irá saltar para a notação matemática muito rapidamente. Se alguma coisa aqui não fizer sentido, envia-me um e-mail.
Update: eu também escrevi sobre como calcular Big-O.
estou pensando em escrever um livro sobre este tópico. Se isto é algo que gostaria de ver, por favor, expresse o seu interesse aqui.