Pressuposto da normalidade da variável dependente
Os independentes teste-t requer que a variável dependente é aproximadamente normalmente distribuída dentro de cada grupo.
Nota: tecnicamente, são os resíduos que precisam ser normalmente distribuídos, mas para um teste t independente, ambos irão dar-lhe o mesmo resultado.,
Você pode testar para isso usando uma série de testes diferentes, mas o teste Shapiro-Wilks de normalidade ou um método gráfico, como um gráfico Q-Q, são muito comuns. Você pode executar estes testes usando estatísticas de SPSS, o procedimento para o qual pode ser encontrado em nosso guia de teste de normalidade. No entanto, o ensaio t é descrito como um ensaio robusto no que diz respeito à presunção de normalidade. Isto significa que algum desvio da normalidade não tem uma grande influência nas taxas de erro do tipo I. A exceção a isso é se a relação entre o menor e o maior tamanho do grupo for maior que 1.,5 (Maior em comparação com menor).
o Que fazer quando você viola a suposição de normalidade
Se você achar que um ou ambos de seu grupo de dados não é aproximadamente normalmente distribuída e grupos de tamanhos diferem muito, você tem duas opções: (1) transformar os dados para que os dados torna-se normalmente distribuídos (para fazer isso no SPSS Statistics veja o nosso guia sobre a Transformação de Dados), ou (2) executar o teste de Mann-Whitney U test, que é um teste não-paramétrico que não requer a suposição de normalidade (para executar este teste em SPSS Statistics veja o nosso guia sobre o teste de Mann-Whitney U Test).,
suposição de homogeneidade da variância
o teste t independente assume que as variâncias dos dois grupos que você está medindo são iguais na população. Se suas variações são desiguais, isso pode afetar a taxa de erro Tipo I. A suposição de homogeneidade da variância pode ser testada usando o teste de igualdade de variâncias de Levene, que é produzido em estatísticas de SPSS ao executar o procedimento de teste t independente., Se você executar o Teste de Levene de Igualdade de Variâncias em SPSS Statistics, você vai obter um resultado semelhante a esse abaixo:

Este teste de homogeneidade de variância fornece uma estatística F e significância valor (p-valor). Estamos principalmente preocupados com o valor significante-se for maior que 0,05 (i.e., p > .05), as variações do nosso grupo podem ser tratadas como iguais. No entanto, se p < 0,05, temos variâncias desiguais e violamos a suposição de homogeneidade das variâncias.,
a Superação de uma violação do pressuposto da homogeneidade de variância
Se o Teste de Levene para Igualdade de Variâncias é estatisticamente significativa, o que indica que o grupo desvios são desigual na população, você pode corrigir para esta violação por não utilizar o pool estimativa para o termo de erro para a estatística t, mas em vez disso, usando um ajuste para o número de graus de liberdade, utilizando de Welch-Satterthwaite método., Em toda a realidade, você provavelmente nunca terá ouvido falar desses ajustes porque as estatísticas de SPSS escondem essa informação e simplesmente rotulam as duas opções como “variâncias iguais assumidas” e “variâncias iguais não assumidas” sem explicitamente indicar os testes subjacentes utilizados., No entanto, você pode ver a evidência destes testes, como abaixo:
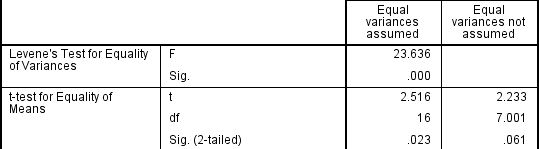
a Partir do resultado do Teste de Levene para Igualdade de Variâncias, podemos rejeitar a hipótese nula de que não existe diferença entre as variâncias entre os grupos e aceitar a hipótese alternativa de que existe uma diferença estatisticamente significativa na variâncias entre os grupos., O efeito de não ser capaz de assumir variações iguais é evidente na coluna final da figura acima, onde vemos uma redução no valor da estatística t e uma grande redução nos graus de liberdade (df). Isto tem o efeito de aumentar o valor p acima do nível de significância crítica de 0,05. Neste caso, portanto, não aceitamos a hipótese alternativa e aceitamos que não existem diferenças estatisticamente significativas entre os meios. Esta não teria sido a nossa conclusão se não tivéssemos testado a homogeneidade das variações.