nós classicamente pensamos na luz como sempre viajando em linhas retas, mas quando as ondas de luz passam perto de uma barreira eles tendem a dobrar – se em torno dessa barreira e se espalhar. Difração de luz ocorre quando uma onda de luz passa por um canto ou através de uma abertura ou fenda que é fisicamente o tamanho aproximado de, ou ainda menor do que o comprimento de onda dessa luz.,

uma demonstração muito simples de difração pode ser conduzida segurando a mão na frente de uma fonte de luz e fechando lentamente dois dedos ao observar a luz transmitida entre eles. À medida que os dedos se aproximam uns dos outros e se aproximam muito, você começa a ver uma série de linhas escuras paralelas aos dedos. As linhas paralelas são na verdade padrões de difração. Este fenômeno também pode ocorrer quando a luz é “dobrada” em torno de partículas que estão na mesma ordem de magnitude que o comprimento de onda da luz., Um bom exemplo disso é a difração da luz solar por nuvens que muitas vezes nos referimos como um lado positivo, ilustrado na Figura 1 com um belo pôr-do-sol sobre o oceano.
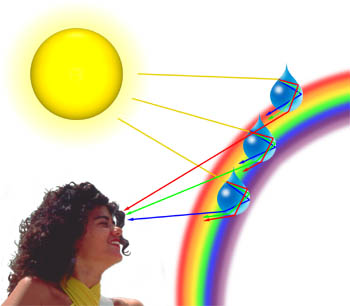
muitas vezes podemos observar tons pastel de azul, rosa, roxo e verde nas nuvens que são geradas quando a luz é difratada a partir de gotas de água nas nuvens. A quantidade de difração depende do comprimento de onda da luz, com comprimentos de onda mais curtos sendo difratados em um ângulo maior do que os maiores (na verdade, luz azul e violeta são difratados em um ângulo maior do que a luz vermelha)., Como uma onda de luz que viaja através da atmosfera encontra uma gota de água, como ilustrado abaixo, ela é primeiramente refratada na água:interface aérea, então é refletida como ela novamente Encontra a interface. O feixe, ainda viajando dentro da gota de água, é mais uma vez refratado como ele atinge a interface por uma terceira vez. Esta última interação com a interface refrata a luz de volta para a atmosfera, mas também difrata uma porção da luz como ilustrado abaixo., Este elemento de difração leva a um fenômeno conhecido como halo de Cellini (também conhecido como o efeito Heiligenschein), onde um anel brilhante de luz envolve a sombra da cabeça do observador.
os Termos difração e dispersão são muitas vezes usados indistintamente e são considerados quase sinônimos. Difraction describes a specialized case of light scattering in which an object with regularly repeating features (such as a diffraction grating) produces an ordered diffraction of light in a diffraction pattern., No mundo real, a maioria dos objetos são muito complexos em forma e devem ser considerados compostos de muitas características de difração individuais que podem coletivamente produzir uma dispersão aleatória de luz.
Um dos conceitos clássicos e mais fundamentais envolvendo difração é o experimento de difração óptica de fenda única, realizado pela primeira vez no início do século XIX. Quando uma onda de luz se propaga através de uma fenda (ou abertura), o resultado depende do tamanho físico da abertura em relação ao comprimento de onda do feixe incidente., Isso é ilustrado na Figura 3 assumindo um conjunto coerente, monocromática de onda emitidos a partir do ponto de origem S, semelhante à luz, que seria produzida por um laser que passa através da abertura d e é difratado, com o principal incidente feixe de luz de aterragem no ponto P e a primeira secundário maxima ocorrendo no ponto Q.
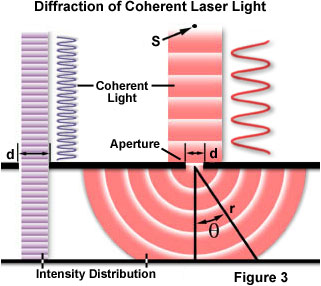
Como mostrado no lado esquerdo da figura, quando o comprimento de onda (λ) é muito menor do que a largura da abertura (d), a onda simplesmente viaja em diante em linha reta, como se fosse uma partícula ou não abertura estavam presentes., No entanto, quando o comprimento de onda excede o tamanho da abertura do diafragma, temos a experiência de difração da luz de acordo com a equação:
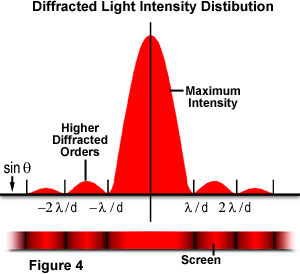
, Onde θ é o ângulo entre o incidente central, direção de propagação e o primeiro mínimo do padrão de difração. O experimento produz um máximo central brilhante que é flanqueado em ambos os lados por máximos secundários, com a intensidade de cada máximo secundário seguinte diminuindo à medida que a distância do centro aumenta. A figura 4 ilustra este ponto com um gráfico de intensidade do feixe versus raio de difração., Note que os mínimos que ocorrem entre os máximos secundários estão localizados em múltiplos de π.
Esta experiência foi explicada pela primeira vez por Augustin Fresnel que, juntamente com Thomas Young, produziu importantes evidências confirmando que a luz viaja em ondas. A partir das figuras acima, vemos como uma luz coerente e monocromática (neste exemplo, iluminação laser) emitida a partir do ponto L é difratada pela abertura D., Fresnel assumido que a amplitude de primeira ordem maxima no ponto Q (definido como eQ) seria dada pela equação:
a, onde A é a amplitude da onda incidente, r é a distância entre d e Q, e f(χ) é uma função de χ, uma inclinação fator introduzido por Fresnel.
difração da luz
explorar como um feixe de luz é difratado quando passa por uma fenda estreita ou abertura. Ajuste o comprimento de onda e tamanho da abertura e observe como isso afeta o padrão de intensidade de difração.,
difração de luz desempenha um papel primordial na limitação da potência de resolução de qualquer instrumento óptico (por exemplo: câmeras, binóculos, telescópios, microscópios e o olho). O poder de resolução é a capacidade do instrumento óptico de produzir imagens separadas de dois pontos adjacentes. Isto é muitas vezes determinado pela qualidade das Lentes e espelhos no instrumento, bem como as propriedades do meio circundante (geralmente ar). A natureza ondulatória da luz força um limite máximo para o poder de resolução de todos os Instrumentos ópticos.,
nossas discussões de difração têm usado uma fenda como a abertura através da qual a luz é difratada. No entanto, todos os Instrumentos ópticos têm aberturas circulares, por exemplo a pupila de um olho ou o diafragma circular e lentes de um microscópio. Aberturas circulares produzem padrões de difração semelhantes aos descritos acima, exceto que o padrão exibe naturalmente uma simetria circular. A análise matemática dos padrões de difração produzidos por uma abertura circular é descrita pela equação:
where θ(1) is the angular position of the first order diffraction minima (the first dark ring), λ is the wavelength of the incident light, d is the diameter of the aperture, and 1.22 is a constant. Na maioria das circunstâncias, o ângulo θ(1) é muito pequena, de forma que a aproximação de que o pecado e tan do ângulo, são quase iguais a produção:
a Partir destas equações, torna-se evidente que o máximo central é diretamente proporcional a λ/d, tornando esta máxima mais espalhadas para comprimentos de onda mais longos e para aberturas menores., The secondary mimina of diffraction set a limit to the useful magnification of objective lenses in optical microscopy, due to inherent difraction of light by these lenses. Por mais perfeita que seja a lente, a imagem de uma fonte pontual de luz produzida pela lente é acompanhada por máximos de ordem secundária e superior. Isto só poderia ser eliminado se a lente tivesse um diâmetro infinito. Dois objetos separados por uma distância inferior a θ(1) não podem ser resolvidos, não importa quão alta a potência da ampliação., Enquanto estas equações foram derivadas para a imagem de uma fonte pontual de luz a uma distância infinita da abertura, é uma aproximação razoável do poder de resolução de um microscópio quando d é substituído pelo diâmetro da objetiva.assim, se dois objetos residem uma distância D um do outro e estão a uma distância L de um observador, o ângulo (expresso em radianos) entre eles é:
o que nos leva a ser capaz de condensar as duas últimas equações a produzir:
em que D(0) é a distância mínima de separação entre os objectos que os permitirá resolver. Usando esta equação, o olho humano pode resolver objetos separados por uma distância de 0.056 milímetros, no entanto, os fotorreceptores na retina não são muito próximos o suficiente para permitir que este grau de resolução e de 0,1 milímetros é mais realista, número, sob circunstâncias normais.
O poder de resolução dos microscópios ópticos é determinado por uma série de fatores, incluindo os discutidos, mas nas circunstâncias mais ideais, este número é de cerca de 0,2 micrômetros., Este número deve ter em conta o alinhamento óptico do microscópio, a qualidade das lentes, bem como os comprimentos de onda predominantes da luz utilizada para a imagem da amostra. Embora muitas vezes não seja necessário calcular o poder de resolução exato de cada objetivo (e seria uma perda de tempo na maioria dos casos), é importante entender as capacidades das lentes de microscópio como eles se aplicam ao mundo real.
autores contribuintes
Mortimer Abramowitz-Olympus America, Inc., Dois Centros Corporativos., Melville, New York, 11747.Michael W., Davidson-National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310.