a Variância mede a distância de um conjunto de dados que está espalhada. Uma variância de zero indica que todos os valores dos dados são idênticos. Todas as variações não-zero são positivas.

uma pequena variância indica que os pontos de dados tendem a ser muito próximos da média, e uns aos outros., Uma alta variância indica que os pontos de dados são muito espalhados a partir da média, e um do outro. Variância é a média das distâncias ao quadrado de cada ponto para a média.

The process of finding the variance is very similar to finding the MAD, mean absolute deviation. a única diferença é a quadratura das distâncias.
Processo: (1) Encontrar a média (média) do conjunto. (2) subtrair cada valor de dados da média para encontrar a sua distância da média. (3) quadrado todas as distâncias. (4) Adicione todos os quadrados das distâncias., (4) dividir pelo número de dados (para a variância da população).

um problema com a variância é que não tem a mesma unidade de medida que os dados originais. Por exemplo, os dados originais que contêm comprimentos medidos em pés têm uma variância medida em pés quadrados.,

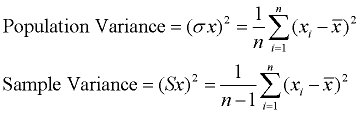Don’t ROUND too soon! When working with the formulas for variance and standard deviation, be careful to avoid rounding too soon., Se o cálculo for feito manualmente, indicar sempre mais casas decimais dentro dos cálculos do que o esperado para o resultado final. Se trabalhar com uma calculadora, levar o valor total das entradas da calculadora até chegar ao resultado final.

o desvio Padrão mostra o quanto de variação (dispersão, espalhar, dispersão) da média existe., Representa um desvio “típico” da média. É uma medida popular da variabilidade porque retorna às unidades originais da medida do conjunto de dados.

um desvio padrão baixo indica que os pontos de dados tendem a ser muito próximos da média. Um elevado desvio-padrão indica que os pontos de dados são distribuídos por uma vasta gama de valores.
O desvio padrão pode ser pensado como uma forma” padrão ” de saber o que é normal (típico), o que é muito grande, e o que é muito pequeno no conjunto de dados.,

O desvio-padrão é uma medida popular de variabilidade porque retorna às unidades originais de medida do conjunto de dados. Por exemplo, os dados originais que contêm comprimentos medidos em pés têm um desvio padrão também medido em pés.,

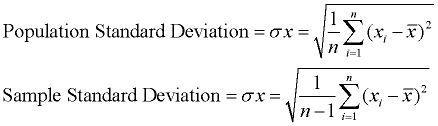Para calcular o desvio padrão pela mão:
O desvio padrão é simplesmente a raiz quadrada da variância.
This description is for computing population standard deviation. Se for necessário um desvio-padrão da amostra, dividir por n – 1 em vez de N., Uma vez que o desvio padrão é a raiz quadrada da variância, devemos primeiro calcular a variância.
1. Encontra o mau.
2. Subtrai a média de cada valor de dados e quadra cada uma destas diferenças (as diferenças ao quadrado).
3. Encontre a média das diferenças ao quadrado (adicione-as e divida pela contagem dos valores dos dados). Esta será a variação.,

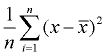desvio
4. Pega na raiz quadrada. Este será o desvio padrão da população. Em torno da resposta de acordo com as direções no problema.

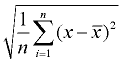desvio padrão

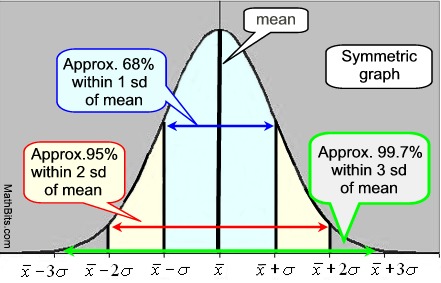
Curva Normal

Uma curva normal é simétrica, curva em forma de sino., O centro do grafo é a média, e a altura e largura do grafo são determinadas pelo desvio padrão. Quando o desvio padrão é pequeno, a curva será alta e estreita em spread. Quando o desvio padrão é grande, a curva será curta e larga em spread. A média e a mediana têm o mesmo valor numa curva normal.

a Curva Normal Regra Empírica:
Aproximadamente …68% dos dados encontram-se dentro de um desvio padrão da média.,95% dos dados situam-se dentro de dois desvios-padrão da média.

• 99,7% dos dados situam-se dentro de três desvios-padrão da média.

IQR para uma curva normal é 1,34896 x desvio padrão.