Introdução
de regressão Linear, também conhecido como regressão linear simples ou bivariadas de regressão linear, é utilizada quando queremos predizer o valor de uma variável dependente com base no valor de uma variável independente. Por exemplo, você pode usar regressão linear para entender se o desempenho do exame pode ser previsto com base no tempo de revisão (i.e.,, sua variável dependente seria “desempenho de exame”, medido a partir de 0-100 Marcos, e sua variável independente seria “tempo de revisão”, medido em horas). Alternadamente, você poderia usar regressão linear para entender se o consumo de cigarro pode ser previsto com base na duração do tabagismo (ou seja, sua variável dependente seria “consumo de cigarro”, medido em termos do número de cigarros consumidos diariamente, e sua variável independente seria “Duração do tabagismo”, medido em dias). Se você tem duas ou mais variáveis independentes, ao invés de apenas uma, você precisa usar regressão múltipla., Alternativamente, se você apenas deseja estabelecer se uma relação linear existe, você pode usar a correlação de Pearson.
nota: a variável dependente é também referida como a variável resultado, alvo ou critério, enquanto a variável independente é também referida como a variável predictor, explicativa ou regressora. Em última análise, seja qual for o termo utilizado, é melhor ser consistente. Referimo-nos a estas como variáveis dependentes e independentes ao longo deste guia.,
neste guia, mostramos-lhe como realizar a regressão linear usando o Stata, bem como interpretar e relatar os resultados deste teste. No entanto, antes de apresentá-lo a este procedimento, você precisa entender os diferentes pressupostos que seus dados devem cumprir para que a regressão linear lhe dê um resultado válido. Vamos discutir estas suposições a seguir.
Stata
pressupostos
existem sete “pressupostos” que sustentam a regressão linear. Se algum destes sete pressupostos não for cumprido, você não pode analisar seus dados usando linear porque você não vai obter um resultado válido., Uma vez que as suposições #1 e #2 se relacionam com a sua escolha de variáveis, elas não podem ser testadas para o uso do Stata. No entanto, você deve decidir se seu estudo atende a essas suposições antes de seguir em frente.hipótese #1: a sua variável dependente deve ser medida ao nível contínuo., Exemplos de tais variáveis contínuas incluem altura (medida em pés e polegadas), temperatura (medida em oC), salário (medido em dólares), revisão de tempo (medido em horas), a inteligência (medido utilizando a pontuação de QI), tempo de reação (medido em milissegundos), teste de desempenho (medido de 0 a 100), vendas (medido em número de transações por mês), e assim por diante. Se não tiver a certeza se a sua variável dependente é contínua (ou seja, medida ao nível do intervalo ou da razão), consulte os nossos tipos de guia variável.,hipótese #2: a sua variável independente Deve ser medida ao nível contínuo ou categórico. No entanto, se você tem uma variável independente categórica, é mais comum usar um teste t independente (para 2 grupos) ou uma ANOVA de Sentido Único (para 3 grupos ou mais). No caso de não ter certeza, exemplos de variáveis categóricas incluem gênero (por exemplo, 2 grupos: masculino e feminino), etnia( por exemplo, 3 grupos: Caucasiano, afro-americano e Hispânico), nível de atividade física( por exemplo, 4 grupos: sedentário, baixo, moderado e alto), e profissão( por ex.,, 5 grupos: cirurgião, médico, enfermeiro, dentista, terapeuta). Neste guia, mostramos-lhe o procedimento de regressão linear e a saída de Stata quando as suas variáveis dependentes e independentes foram medidas em um nível contínuo.
felizmente, você pode verificar suposições #3, #4, #5, #6 e nº7 a usar a Stata. Ao passar aos pressupostos #3, #4, #5, #6 e #7, sugerimos testá-los nesta ordem porque representa uma ordem onde, se uma violação à suposição não for corrigível, você não será mais capaz de usar regressão linear., Na verdade, não se surpreenda se seus dados falham em uma ou mais dessas suposições, uma vez que isso é bastante típico quando se trabalha com dados do mundo real ao invés de exemplos de livros, que muitas vezes só mostram como realizar regressão linear quando tudo corre bem. No entanto, não se preocupe, porque mesmo quando seus dados falham certas suposições, muitas vezes há uma solução para superar isso (por exemplo, transformando seus dados ou usando outro teste estatístico em vez disso)., Lembre-se apenas que se você não verificar se os seus dados correspondem a estas suposições ou se os testar incorrectamente, os resultados que obtém ao executar a regressão linear poderão não ser válidos.
- pressuposto #3: tem de haver uma relação linear entre as variáveis dependentes e independentes. Embora haja uma série de maneiras de verificar se existe uma relação linear entre as suas duas variáveis, sugerimos criar um scatterplot usando o Stata, onde você pode plotar a variável dependente contra a sua variável independente., Você pode então inspeccionar visualmente o scatterplot para verificar a linearidade. O gráfico de dispersão pode ser algo como o seguinte:
Se a relação apresentada no gráfico de dispersão não é linear, você terá que executar uma regressão não-linear de análise ou de “transformação” dos dados, o que você pode fazer usando o Stata.hipótese #4: não deve haver valores anómalos significativos. Os valores anómalos são simplesmente pontos de dados únicos dentro dos seus dados que não seguem o padrão habitual (ex.,, em um estudo de 100 pontuações de QI de alunos, onde a pontuação média foi de 108 com apenas uma pequena variação entre os alunos, um aluno teve uma pontuação de 156, o que é muito incomum, e pode até colocá-la no top 1% das Pontuações de QI globalmente). Os seguintes diagramas de dispersão destacar o potencial de impacto de outliers:
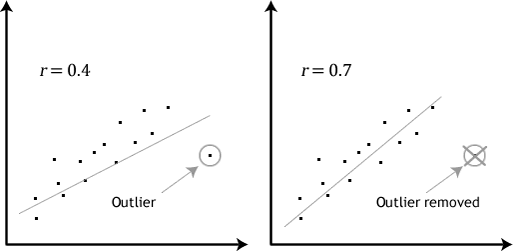
O problema com outliers é que eles podem ter um efeito negativo sobre a equação de regressão é usada para prever o valor da variável dependente com base na variável independente., Isto irá alterar a saída que a Stata produz e reduzir a precisão preditiva dos seus resultados. Felizmente, você pode usar o Stata para realizar diagnósticos em trechos para ajudá-lo a detectar possíveis casos anómalos.
- suposição #5: você deve ter independência das observações, que você pode facilmente verificar usando a estatística de Durbin-Watson, que é um teste simples para executar usando Stata.
- suposição # 6: Seus dados precisam mostrar homoscedasticidade, que é onde as variâncias ao longo da linha de melhor ajuste permanecem semelhantes à medida que você se move ao longo da linha., Os dois diagramas de dispersão a seguir fornecem exemplos simples de dados que atende a este pressuposto e aquele que falha o pressuposto:
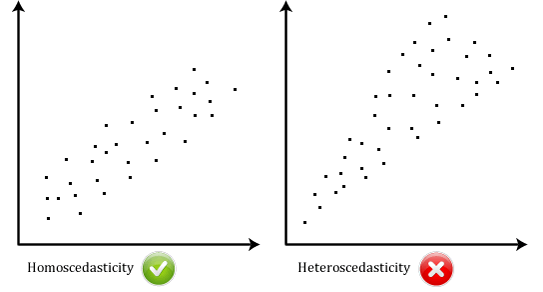
Quando você analisar os seus próprios dados, você vai ter sorte se o gráfico de dispersão parece com qualquer um dos dois acima. Enquanto estes ajudam a ilustrar as diferenças nos dados que se encontram ou violam a suposição de homoscedasticidade, os dados do mundo real são muitas vezes muito mais bagunçados., Você pode verificar se seus dados mostraram homoscedasticidade, traçando os resíduos padronizados de regressão contra o valor previsto padrão de regressão.
- suposição #7: finalmente, você precisa verificar que os resíduos (erros) da linha de regressão estão aproximadamente normalmente distribuídos. Dois métodos comuns para verificar esta suposição incluem o uso de um histograma (com uma curva normal sobreposta) ou um gráfico P-P Normal.
na prática, a verificação das hipóteses #3, #4, #5, #6 e o #7 provavelmente vai ocupar a maior parte do seu tempo quando realizar a regressão linear., No entanto, não é uma tarefa difícil, e a Stata fornece todas as ferramentas que você precisa para fazer isso.
na seção, procedimento, nós ilustramos o procedimento de Stata necessário para realizar regressão linear assumindo que nenhuma suposição foi violada. Em primeiro lugar, definimos o exemplo que usamos para explicar o procedimento de regressão linear no Stata.os estudos mostram que o exercício físico pode ajudar a prevenir doenças cardíacas. Dentro de limites razoáveis, quanto mais você exerce, menos risco você tem de sofrer de doença cardíaca., Uma forma de o exercício reduzir o risco de sofrer de doença cardíaca é reduzindo uma gordura no sangue, chamada colesterol. Quanto mais se exercita, mais baixa a concentração de colesterol. Além disso, tem sido recentemente demonstrado que a quantidade de tempo que você passa assistindo TV – um indicador de um estilo de vida sedentário – pode ser um bom preditor de doenças cardíacas (ou seja, quanto mais TV você assiste, maior o risco de doença cardíaca).,portanto, um pesquisador decidiu determinar se a concentração de colesterol estava relacionada com o tempo gasto assistindo TV em homens saudáveis de 45 a 65 anos (uma categoria de pessoas em risco). Por exemplo, como as pessoas passaram mais tempo assistindo TV, sua concentração de colesterol também aumentou (uma relação positiva); ou o oposto aconteceu? O pesquisador também queria saber a proporção de concentração de colesterol que o tempo gasto assistindo TV poderia explicar, bem como ser capaz de prever a concentração de colesterol., O pesquisador poderia então determinar se, por exemplo, pessoas que passaram oito horas assistindo TV por dia tinham perigosamente altos níveis de concentração de colesterol em comparação com pessoas assistindo apenas duas horas de TV.para realizar a análise, o pesquisador recrutou 100 participantes saudáveis do sexo masculino entre os 45 e os 65 anos. A quantidade de tempo gasto assistindo TV (por exemplo, a variável independente, time_tv) e concentração de colesterol (por exemplo, a variável dependente, o colesterol) foram registrados para todos os 100 participantes., Expresso em termos variáveis, o pesquisador queria regredir o colesterol no time_tv.
Nota: O exemplo e os dados utilizados para este guia são fictícios. Acabamos de criá-los para os propósitos deste guia.
Stata
Setup in Stata
Nota: não importa se você cria a variável dependente ou independente primeiro.
Depois de criar estas duas variáveis-time_tv e colesterol – introduzimos as pontuações para cada uma das duas colunas da folha de cálculo (Edit) do Editor de dados (i.e., o tempo em horas que os participantes assistiram a TV na coluna da esquerda (isto é, time_tv, a variável independente), e dos participantes colesterol concentração em mmol/L na coluna do lado direito (por exemplo, o colesterol, a variável dependente), como mostrado abaixo:
Publicado com a permissão por escrito de StataCorp LP.,
Stata
procedimento de ensaio em Stata
nesta secção, mostramos – lhe como analisar os seus dados usando regressão linear no Stata quando os seis pressupostos da secção anterior, pressupostos, não foram violados. Você pode realizar regressão linear usando código ou interface gráfica de usuário do Stata (GUI). Depois de ter realizado a sua análise, mostramos-lhe como interpretar os seus resultados. Em primeiro lugar, escolha se deseja usar o código ou a interface gráfica de utilizador do Stata (GUI).,
Código
O código para realizar a regressão linear dos dados assume a forma:
regress DependentVariable IndependentVariable
Este código é inserido na tag caixa abaixo:
Publicado com a permissão por escrito de StataCorp LP.,
Usando o nosso exemplo, onde a variável dependente é o colesterol e a variável independente é time_tv, o código seria:
regress colesterol time_tv
Nota 1: o que Você precisa para ser mais preciso quando introduzir o código dentro da tag caixa. O código é “case sensitive”. Por exemplo, se você digitar “colesterol” onde o ” C ” é maiúsculo em vez de minúsculas (i.e., um pequeno “c”), que deve ser, você receberá uma mensagem de erro como o seguinte:
Nota 2: Se você ainda estiver recebendo a mensagem de erro na Nota 2 acima, vale a pena conferir o nome que você deu a duas variáveis, no Editor de Dados quando você configurar o arquivo (por exemplo, ver o Editor de Dados tela acima)., caixa no lado direito do Editor de Dados de ecrã, esta é a maneira que você soletrou seu variáveis
seção, não o
secção que você precisa inserir o código (ver, abaixo, a nossa variável dependente). Isto pode parecer óbvio, mas é um erro que às vezes é feito, resultando no erro na Nota 2 acima.
portanto, digite o código, regresse o colesterol time_tv, e pressione o botão “Return / Enter” no seu teclado.,
publicado com autorização por escrito da StataCorp LP.
pode ver a saída de Stata que será produzida aqui.,
Interface de Utilizador Gráfica (GUI)
Os três passos necessários para realizar a regressão linear na Stata 12 e 13 são mostrados abaixo:
- Clique em Estatísticas > modelos Lineares e relacionados > regressão Linear no menu principal, como mostrado abaixo:
Publicado com a permissão por escrito de StataCorp LP.,
Você será presenteado com a Regredir – regressão Linear caixa de diálogo:
Publicado com a permissão por escrito de StataCorp LP.
- Seleccione o colesterol dentro da variável dependente: lista e o time_tv dentro das variáveis independentes: lista. Você vai acabar com a seguinte tela:
publicado com permissão por escrito do StataCorp LP.,
-
Clique em
botão. Isto irá gerar a saída.
Stata
a Saída da análise de regressão linear no Stata
Se os dados passados pressuposto #3 (i.é., não houve uma relação linear entre as duas variáveis), #4 (i.é., não houve casos isolados), assunção #5 (i.é, você tinha independência das observações), assunção #6 (i.é., os dados mostraram homocedasticidade) e a assunção #7 (i.e.,, resíduos (erros) foram de aproximadamente normalmente distribuída), que explicamos anteriormente nos Pressupostos seção, você só vai precisar para interpretar a seguinte regressão linear de saída do Stata:
Publicado com a permissão por escrito de StataCorp LP.,
A saída consiste de quatro importantes peças de informação: (a) o valor de R2 (R-squared” linha) representa a proporção da variação na variável dependente que pode ser explicada pela nossa variável independente (tecnicamente é a proporção de variação explicada pelo modelo de regressão acima da média do modelo). No entanto, R2 é baseado na amostra e é uma estimativa positivamente tendenciosa da proporção da variância da variável dependente contabilizada pelo modelo de regressão (i.e.,, ele é muito grande); (b) um R2 ajustado valor (“Adj R-squared” linha), que corrige o viés positivo para fornecer um valor que seria esperado na população; (c) o valor F, graus de liberdade (“F( 1, 98)”) e a significância estatística do modelo de regressão (“Prob > F” linha”); e (d) os coeficientes para a constante e variável independente (“Coeficiente.”coluna), que é a informação que você precisa para prever a variável dependente, colesterol, usando a variável independente, time_tv.
neste exemplo, R2 = 0. 151. R2 ajustado = 0, 143 (para 3 d. p.,), o que significa que a variável independente, time_tv, explica 14.3% da variabilidade da variável dependente, colesterol, na população. O R2 ajustado é também uma estimativa do tamanho do efeito, que em 0,143 (14,3%), é indicativo de um tamanho do efeito médio, de acordo com a classificação de Cohen (1988). No entanto, normalmente é o R2 que não é o R2 ajustado que é reportado nos resultados. Neste exemplo, o modelo de regressão é estatisticamente significante, F (1, 98) = 17,47, p = .0001., Isto indica que, em geral, o modelo aplicado pode prever estatisticamente significativamente a variável dependente, o colesterol.
Nota: apresentamos a saída da análise de regressão linear acima. No entanto, uma vez que você deve ter testado seus dados para as suposições que explicamos anteriormente na seção de suposições, você também terá que interpretar a saída de Stata que foi produzida quando você testou para essas suposições. Isto inclui: (a) o scatterplots que você usou para verificar se havia uma relação linear entre suas duas variáveis (i.e., Pressuposto #3); (b) casewise diagnósticos para verificar se havia diferença significativa de valores atípicos (por exemplo, Pressuposto #4); (c) a saída de Durbin-Watson estatística para verificar a independência das observações (por exemplo, Pressuposto #5); (d) um gráfico de dispersão de regressão resíduo padronizado contra a regressão padronizados do valor previsto para determinar se os dados mostraram homocedasticidade (i.é., Pressuposto #6); e um histograma (sobreposta curva normal) e Normal P-P Plot para verificar se os resíduos (erros) foram de aproximadamente normalmente distribuída (i.é., Pressuposto #7)., Além disso, lembre-se que, se os seus dados falharem em algum destes pressupostos, a saída que obtém do procedimento de regressão linear (ou seja, a saída que discutimos acima) deixará de ser relevante, e poderá ter de realizar um teste estatístico diferente para analisar os seus dados.,
Stata
Relatório a saída da análise de regressão linear
Quando você relatar a saída do seu regressão linear, é uma boa prática incluir: (a) uma introdução à análise realizada; (b) informação sobre o seu amostra, incluindo quaisquer valores em falta; c) a F observada-valor graus de liberdade e nível de significância (i.é., o valor de p); (d) a percentagem da variabilidade na variável dependente explicada pela variável independente (por exemplo, o R2 Ajustado ); e (e) a equação de regressão para o modelo., Com base nos resultados acima, podemos relatar os resultados do presente estudo, como a seguir:
- Geral
Uma regressão linear, estabeleceu que o tempo diário gasto assistindo TV poderia estatisticamente significativo de prever a concentração de colesterol, F(1, 98) = 17.47, p = .O 0001 e o tempo gasto assistindo TV representaram 14,3% da variabilidade explicada na concentração de colesterol. A equação de regressão foi: concentração de colesterol prevista = -2, 135 + 0, 044 x (tempo gasto assistindo tv).,
para além da notificação dos resultados acima referidos, pode ser utilizado um diagrama para apresentar visualmente os seus resultados. Por exemplo, você poderia fazer isso usando um scatterplot com intervalos de confiança e previsão (embora não seja muito comum adicionar o último). Isto pode tornar mais fácil para os outros compreenderem os seus resultados. Além disso, você pode usar sua equação de regressão linear para fazer previsões sobre o valor da variável dependente com base em diferentes valores da variável independente., Embora o Stata não produza esses valores como parte do procedimento de regressão linear acima, há um procedimento no Stata que você pode usar para fazê-lo.