wariancja mierzy, jak daleko zestaw danych jest rozłożony. Wariancja zera oznacza, że wszystkie wartości danych są identyczne. Wszystkie niezerowe wariancje są dodatnie.

mała wariancja wskazuje, że punkty danych są bardzo zbliżone do średniej i do siebie., Wysoka wariancja wskazuje, że punkty danych są bardzo rozłożone od średniej i od siebie. Wariancja to średnia kwadratowych odległości od każdego punktu do średniej.

proces znajdowania wariancji jest bardzo podobny do znajdowania szalonego, średniego odchylenia bezwzględnego.
jedyną różnicą jest wyrównanie odległości.
Process: (1) Find The mean (average) of the set. (2) Odejmij każdą wartość danych od średniej, aby znaleźć jej odległość od średniej. (3) kwadrat Wszystkie odległości. (4) Dodaj wszystkie kwadraty odległości., (4) podzielić przez liczbę sztuk danych(dla wariancji populacji).

jeden problem z wariancją jest to, że nie ma tej samej jednostki miary, co oryginalne dane. Na przykład oryginalne dane zawierające długości mierzone w stopach mają wariancję mierzoną w stopach kwadratowych.,

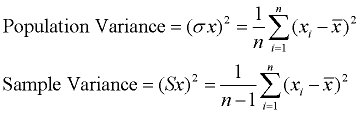Don’t ROUND too soon! When working with the formulas for variance and standard deviation, be careful to avoid rounding too soon., W przypadku ręcznego obliczania zawsze należy umieścić w obliczeniach więcej miejsc po przecinku niż oczekiwano dla wyniku końcowego. Jeśli pracujesz z kalkulatorem, noś pełną wartość wpisów kalkulatora, aż do uzyskania ostatecznego wyniku.

odchylenie standardowe pokazuje, ile zmienności (dyspersja, rozproszenie, rozproszenie) od średniej istnieje., Stanowi „typowe” odchylenie od średniej. Jest to popularna miara zmienności, ponieważ powraca do oryginalnych jednostek miary zbioru danych.

niskie odchylenie standardowe wskazuje, że punkty danych są bardzo zbliżone do średniej. Wysokie odchylenie standardowe wskazuje, że punkty danych są rozłożone na duży zakres wartości.
odchylenie standardowe można traktować jako „standardowy” sposób poznania tego, co jest normalne( typowe), co jest bardzo duże, a co jest bardzo małe w zbiorze danych.,

odchylenie standardowe jest popularną miarą zmienności, ponieważ powraca do oryginalnych jednostek miary zbioru danych. Na przykład oryginalne dane zawierające długości mierzone w stopach mają odchylenie standardowe również mierzone w stopach.,

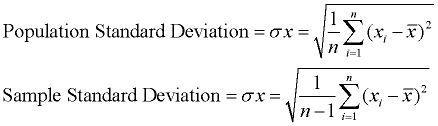aby obliczyć odchylenie standardowe ręcznie:
odchylenie standardowe jest po prostu pierwiastkiem kwadratowym wariancji.
opis ten służy do obliczania odchylenia standardowego populacji. Jeśli wymagane jest odchylenie standardowe próbki, podziel przez n – 1 zamiast N., Ponieważ odchylenie standardowe jest pierwiastkiem kwadratowym wariancji, musimy najpierw obliczyć wariancję.
1. Znajdź wrednego.
2. Odjąć średnią z każdej wartości danych i kwadrat każdej z tych różnic(kwadratowe różnice).
3. Znajdź średnią z kwadratowych różnic (dodaj je i podziel przez liczbę wartości danych). To będzie wariancja.,

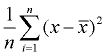wariancja
4. Weź pierwiastek kwadratowy. Będzie to odchylenie standardowe populacji. Zaokrągl odpowiedź zgodnie ze wskazówkami w problemie.

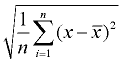odchylenie standardowe

iv id

krzywa normalna

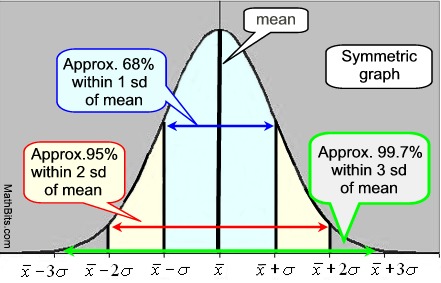
krzywa normalna jest krzywą symetryczną, w kształcie dzwonu., Środek wykresu jest średnią, a wysokość i szerokość wykresu są określone przez odchylenie standardowe. Gdy odchylenie standardowe jest małe, Krzywa będzie wysoka i wąska. Gdy odchylenie standardowe jest duże, Krzywa będzie krótka i szeroka. Średnia i mediana mają tę samą wartość w krzywej normalnej.

Norma krzywej normalnej:
w przybliżeniu …

• 68% danych mieści się w granicach jednego odchylenia standardowego średniej.,

• 95% danych mieści się w granicach dwóch odchyleń standardowych od średniej.

• 99,7% danych mieści się w granicach trzech odchyleń standardowych od średniej.

IQR dla krzywej normalnej wynosi 1,34896 x odchylenie standardowe.