Support Vector Machine lub SVM jest jednym z najpopularniejszych algorytmów uczenia nadzorowanego, który jest używany do klasyfikacji, a także problemów regresji. Jednak przede wszystkim jest on używany do problemów klasyfikacji w uczeniu maszynowym.
celem algorytmu SVM jest stworzenie najlepszej linii lub granicy decyzyjnej, która może segregować n-wymiarową przestrzeń na klasy, abyśmy mogli łatwo umieścić nowy punkt danych w odpowiedniej kategorii w przyszłości., Ta najlepsza granica decyzyjna nazywana jest hiperplaną.
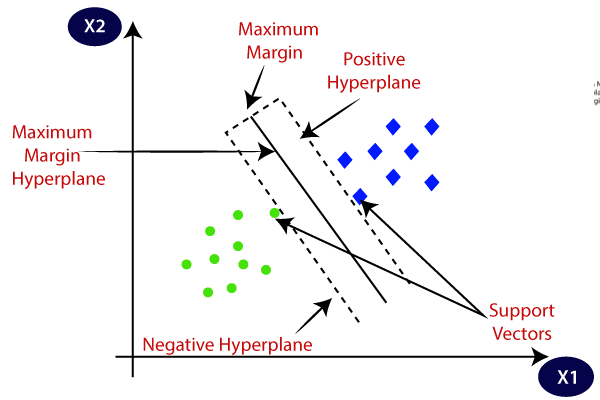
SVM wybiera skrajne punkty/wektory, które pomagają w tworzeniu hiperplany. Te skrajne przypadki są nazywane wektorami wsparcia, a więc algorytm jest określany jako maszyna wektorowa wsparcia. Rozważ poniższy diagram, w którym istnieją dwie różne kategorie, które są klasyfikowane za pomocą granicy decyzji lub hiperplany:
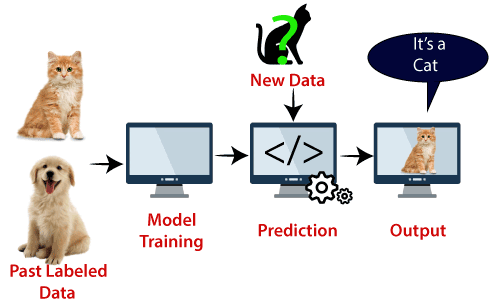
przykład: SVM można zrozumieć za pomocą przykładu, którego użyliśmy w klasyfikatorze KNN., Załóżmy, że widzimy dziwnego kota, który ma również pewne cechy psów, więc jeśli chcemy model, który może dokładnie zidentyfikować, czy jest to kot czy pies, więc taki model można utworzyć za pomocą algorytmu SVM. Najpierw wytrenujemy nasz model z mnóstwem zdjęć kotów i psów, aby mógł poznać różne cechy kotów i psów, a następnie testujemy go z tym dziwnym stworzeniem. Tak więc, jak wektor wsparcia tworzy granicę decyzyjną między tymi dwoma danymi (kot i pies) i wybiera skrajne przypadki (wektory wsparcia), zobaczy skrajny przypadek kota i psa., Na podstawie wektorów podporowych klasyfikuje go jako kot. Rozważ poniższy diagram:
algorytm SVM może być używany do wykrywania twarzy, klasyfikacji obrazu, kategoryzacji tekstu itp.
typy SVM
SVM mogą być dwóch typów:
- Linear SVM: Linear SVM jest używany do liniowo rozdzielalnych danych, co oznacza, że jeśli zbiór danych można podzielić na dwie klasy za pomocą pojedynczej linii prostej, to takie dane są określane jako liniowo rozdzielalne dane, a klasyfikator jest używany jako liniowy klasyfikator SVM.,
- nieliniowa SVM: nieliniowa SVM jest używana do nieliniowych oddzielonych danych, co oznacza, że jeśli zbiór danych nie może być klasyfikowany za pomocą linii prostej, to takie dane są określane jako nieliniowe dane, a klasyfikator używany jest nazywany nieliniowym klasyfikatorem SVM.
Hiperplaneta i Wektory pomocnicze w algorytmie SVM:
Hiperplaneta: może być wiele linii/granic decyzji, aby segregować klasy w n-wymiarowej przestrzeni, ale musimy znaleźć najlepszą granicę decyzji, która pomaga klasyfikować punkty danych. Ta najlepsza granica jest znana jako hyperplane SVM.,
Wymiary hyperplane zależą od cech obecnych w zbiorze danych, co oznacza, że jeśli są 2 cechy (jak pokazano na obrazku), to hyperplane będzie linią prostą. A jeśli są 3 Funkcje, To hyperplane będzie płaszczyzną dwuwymiarową.
zawsze tworzymy hiperplanę, która ma maksymalny margines, czyli maksymalną odległość między punktami danych.
Wektory nośne:
punkty danych lub wektory, które są najbliżej hiperplany i które wpływają na położenie hiperplany, są określane jako wektory nośne., Ponieważ wektory te wspierają hiperplanę, stąd nazywany jest wektorem nośnym.
jak działa SVM?
Linear SVM:
działanie algorytmu SVM można zrozumieć za pomocą przykładu. Załóżmy, że mamy zbiór danych, który ma dwa znaczniki (zielony i niebieski), a zbiór danych ma dwie funkcje x1 i x2. Chcemy klasyfikatora, który może sklasyfikować parę (x1, x2) współrzędnych w kolorze zielonym lub niebieskim. Rozważ poniższy obrazek:
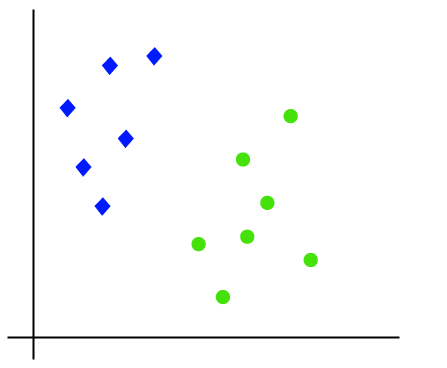
ponieważ jest to przestrzeń 2-d, więc używając prostej linii, możemy łatwo rozdzielić te dwie klasy., Ale może być wiele linii, które mogą oddzielić te klasy. Rozważ poniższy obrazek:
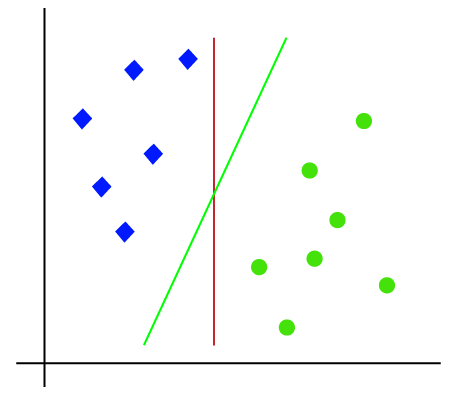
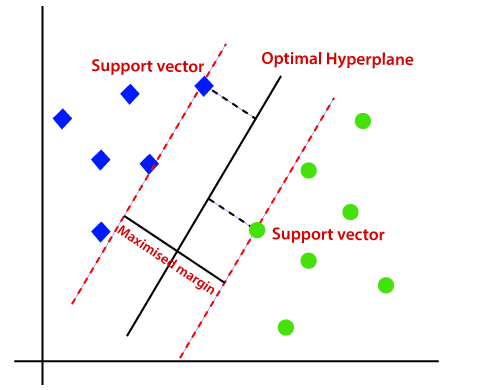
dlatego algorytm SVM pomaga znaleźć najlepszą linię lub granicę decyzji; ta najlepsza granica lub region nazywa się hiperplaną. Algorytm SVM znajduje najbliższy punkt linii z obu klas. Punkty te nazywane są wektorami wsparcia. Odległość między wektorami a hiperplaną nazywa się marginesem. Celem SVM jest maksymalizacja tej marży. Hiperplane o maksymalnym marginesie nazywa się hiperplaną optymalną.,
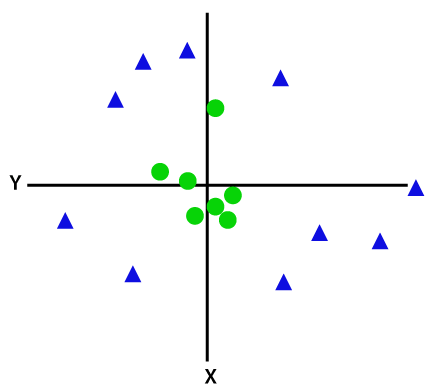
nieliniowa SVM:
Jeśli dane są ułożone liniowo, możemy je oddzielić za pomocą linii prostej, ale dla danych nieliniowych nie możemy narysować pojedynczej linii prostej. Rozważ poniższy obrazek:
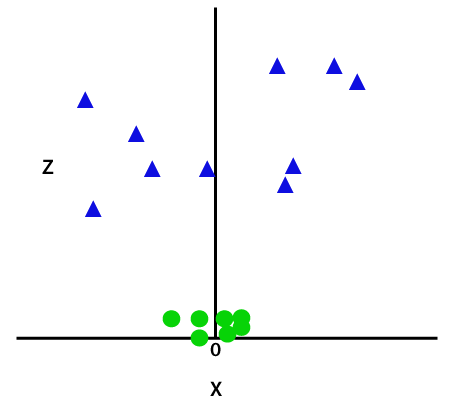
aby oddzielić te punkty danych, musimy dodać jeszcze jeden wymiar. Dla danych liniowych użyliśmy dwóch wymiarów x i y, więc dla danych nieliniowych dodamy trzeci wymiar z., Można go obliczyć jako:
z=x2 +y2
dodając trzeci wymiar, przestrzeń próbki stanie się jak na poniższym obrazku:
tak więc teraz SVM podzieli zbiory danych na klasy w następujący sposób. Rozważ poniższy obrazek:
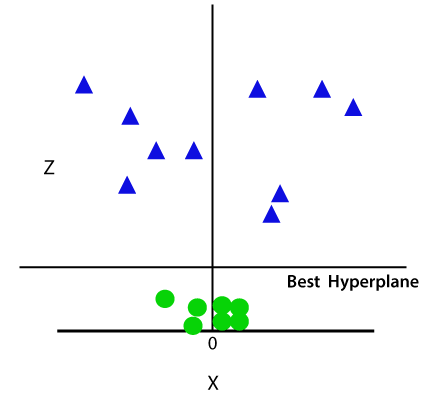
ponieważ znajdujemy się w przestrzeni 3D, stąd wygląda on jak płaszczyzna równoległa do osi X. Jeśli przekonwertujemy go w przestrzeni 2d z = 1, to będzie on wyglądał następująco:
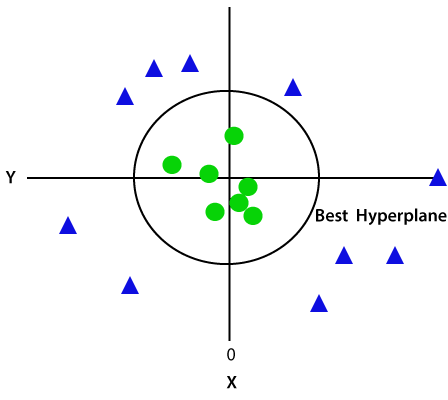
stąd otrzymujemy Obwód promienia 1 w przypadku danych nieliniowych.,
implementacja Pythona Maszyny wektorowej wsparcia
teraz zaimplementujemy algorytm SVM używając Pythona. Tutaj użyjemy tego samego zestawu danych user_data, który wykorzystaliśmy w regresji logistycznej i klasyfikacji KNN.
- etap wstępnego przetwarzania danych
do momentu wstępnego przetwarzania danych Kod pozostanie taki sam. Poniżej znajduje się kod:
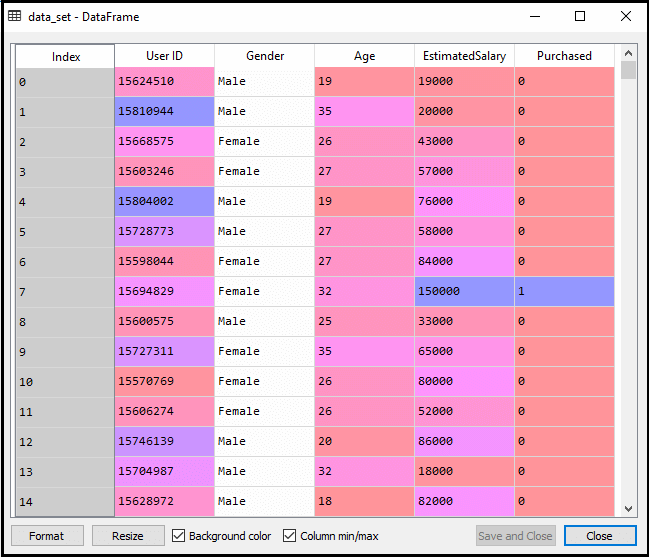
Po wykonaniu powyższego kodu wstępnie przetworzymy dane., Kod da zestaw danych jako:
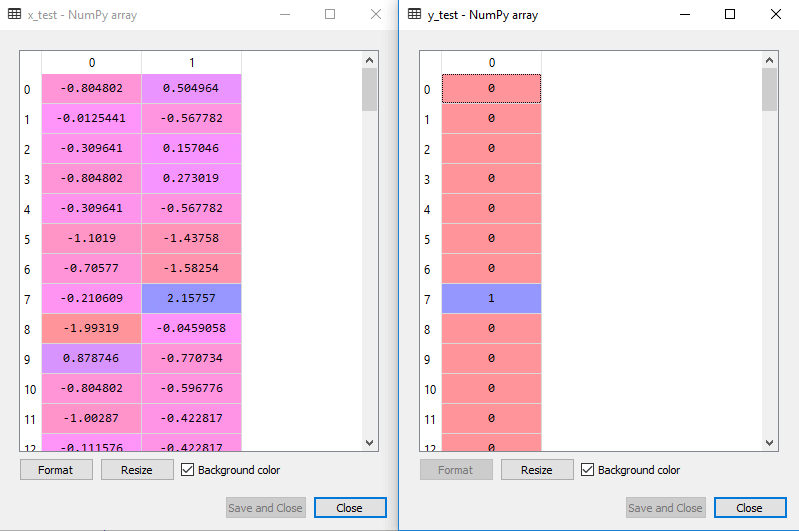
skalowane wyjście dla zestawu testowego będzie:
dopasowanie klasyfikatora SVM do zestawu treningowego:
teraz zestaw treningowy zostanie dopasowany do klasyfikatora SVM. Aby utworzyć klasyfikator SVM, zaimportujemy klasę SVC ze sklepu.biblioteka svm. Poniżej znajduje się jego kod:
w powyższym kodzie użyliśmy kernel=’linear', ponieważ tutaj tworzymy SVM dla liniowo rozdzielalnych danych. Możemy go jednak zmienić na dane nieliniowe., Następnie dopasowaliśmy klasyfikator do zestawu danych treningowych (x_train, y_train)
wyjście:
wydajność modelu można zmienić, zmieniając wartość C(Współczynnik regularyzacji), gamma i jądra.
- przewidywanie wyniku zestawu testowego:
Teraz przewidujemy wynik dla zestawu testowego. W tym celu utworzymy nowy wektor y_pred. Poniżej znajduje się jego kod:
Po pobraniu wektora y_pred, możemy porównać wynik y_pred i y_test, aby sprawdzić różnicę między rzeczywistą wartością a przewidywaną wartością.,
wyjście: Poniżej znajduje się wyjście do przewidywania zestawu testowego:

- Tworzenie macierzy zamieszania:
teraz zobaczymy wydajność klasyfikatora SVM, że ile jest błędnych prognoz w porównaniu do klasyfikatora regresji logistycznej. Aby utworzyć macierz zamieszania, musimy zaimportować funkcję confusion_matrix biblioteki sklearn. Po zaimportowaniu funkcji wywołamy ją za pomocą nowej zmiennej cm. Funkcja przyjmuje dwa parametry, głównie y_true (wartości rzeczywiste) i y_pred (wartość docelowa zwracana przez klasyfikator)., Poniżej znajduje się jego kod:
Wyjście:
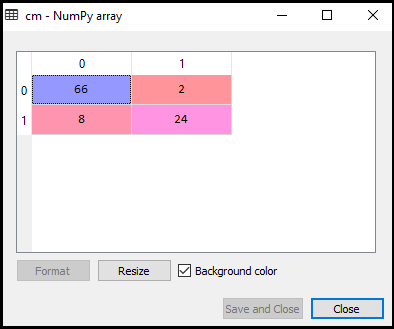
jak widać na powyższym obrazku wyjściowym, istnieje 66+24= 90 poprawnych prognoz i 8+2= 10 poprawnych prognoz. Dlatego możemy powiedzieć, że nasz model SVM poprawił się w porównaniu z modelem regresji logistycznej.,
- Wizualizacja wyniku zestawu treningowego:
Teraz wizualizujemy wynik zestawu treningowego, poniżej znajduje się jego kod:
Wyjście:
wykonując powyższy kod, otrzymamy wyjście:
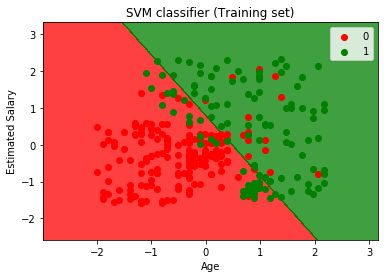
jak widzimy, powyższe wyjście wygląda podobnie do wyjścia regresji logistycznej. W wyjściu mamy linię prostą jako hiperplane, ponieważ użyliśmy jądra liniowego w klasyfikatorze. Omówiliśmy również powyżej, że dla przestrzeni 2d hiperplan w SVM jest linią prostą.,
- Wizualizacja wyniku zestawu testowego:
Wyjście:
wykonując powyższy kod, otrzymamy wyjście:
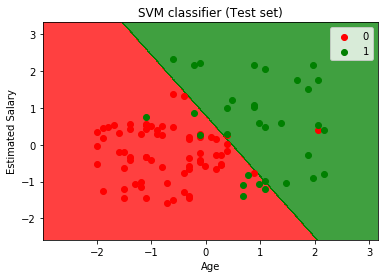
jak widać na powyższym obrazku wyjściowym, klasyfikator SVM podzielił użytkowników na dwa regiony (zakupione lub nie zakupione). Użytkownicy, którzy kupili SUV, znajdują się w czerwonym regionie z czerwonymi punktami scatter. A użytkownicy, którzy nie kupili Suva, są w zielonym regionie z zielonymi punktami scatter. Hyperplane podzielił dwie klasy na zakupioną i nie zakupioną zmienną.