jest to pierwsza z serii trzech postów. Drugi post mówi o tym, jak obliczyć Big-O. trzeci artykuł mówi o zrozumieniu formalnej definicji Big-O.
notacja Big-O była dla mnie naprawdę strasznym pojęciem. Myślałem, że tak” prawdziwi ” Programiści mówili o swoim kodzie. To wszystko było bardziej przerażające, ponieważ akademickie opisy (takie jak Wikipedia) miały dla mnie bardzo mały sens. Jest to frustrujące, ponieważ podstawowe koncepcje nie są w rzeczywistości takie trudne.,
Mówiąc najprościej, notacja Big-O jest tym, jak programiści mówią o tym, co się dzieje. Algorytmy to kolejny przerażający temat, który poruszę w innym poście, ale dla naszych celów powiedzmy, że „algorytm” oznacza funkcję w twoim programie (która nie jest zbyt odległa). Duża Onotacja funkcji zależy od tego, jak reaguje ona na różne wejścia. Ile jest wolniej, jeśli damy mu listę 1000 rzeczy do pracy zamiast listy 1 rzeczy?
rozważ ten kod:
def item_in_list(to_check, the_list): for item in the_list: if to_check == item: return True return False
więc jeśli wywołamy tę funkcję jakitem_in_list(2, ), powinna być dość szybka., Zapętlamy każdą rzecz z listy i jeśli znajdziemy pierwszy argument naszej funkcji, zwracamy True. Jeśli dotrzemy do końca I go nie znajdziemy, zwróć False.
„złożoność” tej funkcji to O(n). Za chwilę wyjaśnię, co to oznacza, ale rozwalmy to matematycznie. O(n) jest odczytywana „kolejność N”, ponieważ funkcja O jest również znana jako funkcja Order. Myślę, że to dlatego, że robimy aproksymację, która zajmuje się „rzędami wielkości”.,
„rzędy wielkości” to kolejny termin matematyczny, który zasadniczo określa różnicę między klasami liczb. Pomyśl o różnicy między 10 a 100. Jeśli wyobrażasz sobie 10 swoich bliskich i 100 osób, to naprawdę duża różnica. Podobnie różnica między 1000 a 10 000 jest dość duża (w rzeczywistości różnica między samochodem junker a lekko używanym). Okazuje się, że w przybliżeniu,tak długo, jak jesteś w rząd wielkości, jesteś dość blisko., Gdybyś zgadł liczbę gumballi w maszynie, byłbyś w granicach rzędu wielkości, gdybyś powiedział 200gumballi. 10,000 gumballi to by było na tyle.

Rysunek 1: maszyna gumballowa, której liczba gumballi prawdopodobnie mieści się w rzędzie wielkości 200.
powrót do sekcjiO(n), mówi to, że gdybyśmy mieli wykreślić czas potrzebny na uruchomienie tej funkcji z wejściami o różnej wielkości (np. obraz 1 pozycji, 2 pozycji, 3 pozycji, itd.), zobaczylibyśmy, że odpowiada on mniej więcej liczbie pozycji w tablicy., Jest to wykres liniowy. Oznacza to, że linia jest w zasadzie prostowata, jeśli chcesz ją wykreślić.
niektórzy z Was zapewne zauważyli, że gdyby w powyższym przykładzie kodu ouritem był zawsze pierwszą pozycją na liście, nasz kod byłby naprawdę szybki! To prawda, ale Big-O polega na przybliżonym najgorszym przypadku robienia czegoś. Najgorsze dla powyższego kodu jest to, że rzecz, której szukamy, w ogóle nie znajduje się na liście. (Uwaga: termin matematyczny to „górna granica”, co oznacza mówienie o matematycznej granicy awfulness).,
Jeśli chcesz zobaczyć wykres dla tych funkcji, ignorujesz funkcję O()I zmieniasz zmienną n dla x. Następnie możesz wpisać To Do Wolfram Alpha jako „plot x”, który pokaże Ci przekątną. Powodem, dla którego zamieniasz n na x, jest to, że ich program graficzny używa x jako nazwy zmiennej, ponieważ odpowiada xaxis. Oś x coraz większa od lewej do prawej odpowiada tworzeniu coraz większych tablic do funkcji., Osi y przedstawia czas, więc im wyższa linia, tym wolniejsza.
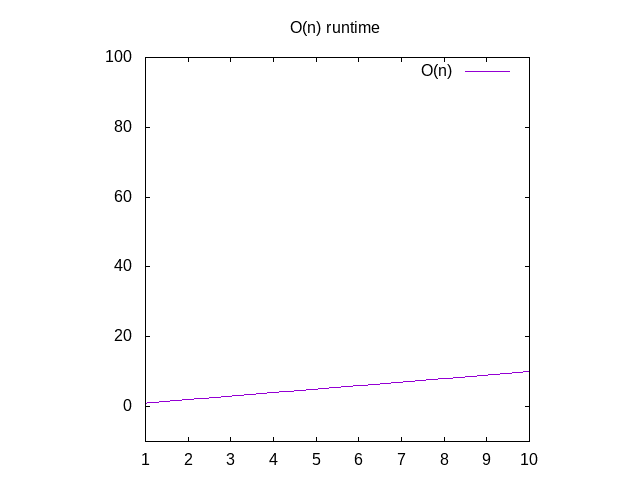
Rysunek 2: Charakterystyka Runtime funkcji O(n)
więc jakie są inne przykłady tego?
rozważ tę funkcję:
def is_none(item): return item is None
jest to trochę głupi przykład, ale proszę mi wybaczyć. Ta funkcja jest wywołana O(1), która nazywa się”constant time”. Oznacza to, że to, jak duży jest nasz wkład, zawsze zajmuje tyle samo czasu, aby obliczyć rzeczy., Jeśli wrócisz do Wolframa i plot 1, zobaczysz, że zawsze pozostaje taki sam, bez względu na to, jak daleko w prawo idziemy. Jeśli przechodzisz na listę 1 miliona liczb całkowitych, zajmie to mniej więcej tyle samo czasu, jeśli zamierzasz przejść na listę 1 liczby całkowitej. Stały czas jest uważany za najlepszy scenariusz dla funkcji.
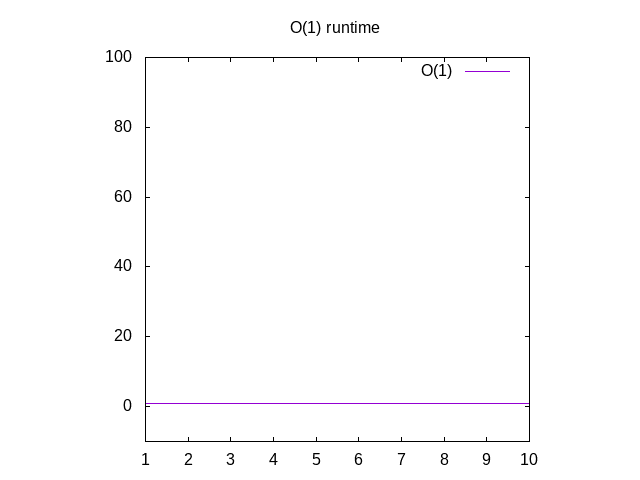
Rysunek 3: charakterystyka działania funkcji O(1)
rozważ tę funkcję:
poniżej znajduje się porównanie każdego z tych wykresów, dla odniesienia., Widać, że funkcja O(n^2) będzie bardzo szybko powolna, ponieważ coś, co działa w stałym czasie, będzie znacznie lepsze. Jest to szczególnie przydatne, jeśli chodzi o struktury danych, o których wkrótce napiszę.
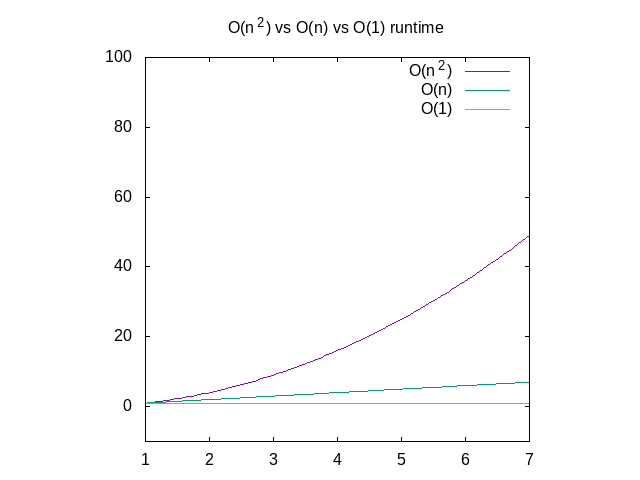
Rysunek 4: Porównanie funkcji o(n2) vs O(n) vs o(1)
jest to dość wysoki przegląd notacji Big-O, ale mam nadzieję, że zapoznałeś się z tym tematem., Istnieje kurs coursera, który może dać ci bardziej dogłębny wgląd w ten temat, ale ostrzegam, że bardzo szybko przeskoczy do notacji matematycznej. Jeśli coś tu nie ma sensu, wyślij mi maila.
aktualizacja: pisałem też o tym, jak obliczyć Big-O.
myślę o napisaniu książki na ten temat. Jeśli jest to coś, co chciałbyś zobaczyć, proszę wyrazić swoje zainteresowanie tym tutaj.