założenie normalności zmiennej zależnej
niezależny test t wymaga, aby zmienna zależna była w przybliżeniu normalnie rozłożona w każdej grupie.
Uwaga: technicznie, to pozostałości, które muszą być normalnie rozłożone, ale dla niezależnego testu t, oba dadzą ten sam wynik.,
można to sprawdzić za pomocą wielu różnych testów, ale bardzo często stosuje się test normalności Shapiro-Wilksa lub metodę graficzną, taką jak Wykres Q-Q. Możesz uruchomić te testy za pomocą statystyk SPSS, których procedurę można znaleźć w naszym Przewodniku testowanie normalności. Jednak test t jest opisany jako solidny test w odniesieniu do założenia normalności. Oznacza to, że pewne odchylenia od normalności nie mają dużego wpływu na poziom błędów typu I. Wyjątkiem jest sytuacja, gdy stosunek najmniejszej do największej wielkości grupy jest większy niż 1.,5 (największy w porównaniu do najmniejszego).
co zrobić, gdy naruszasz założenie normalności
Jeśli stwierdzisz, że jedno lub oba dane twojej grupy nie są w przybliżeniu rozkładane normalnie, a rozmiary grup znacznie się różnią, masz dwie opcje: (1) przekształć swoje dane tak, aby dane stały się rozkładane normalnie (aby to zrobić w statystykach SPSS zobacz nasz przewodnik po przekształcaniu danych) lub (2) Uruchom test Manna-Whitneya U, który jest nieparametrycznym testem, który nie wymaga założenia normalności (aby uruchomić ten test w statystykach SPSS zobacz nasz przewodnik po Mann-Whitney U test).,
założenie jednorodności wariancji
niezależny test t zakłada, że wariancje dwóch mierzonych grup są równe w populacji. Jeśli różnice są nierówne, może to wpłynąć na poziom błędu typu I. Założenie jednorodności wariancji może być przetestowane za pomocą testu równości wariancji Levene ' a, który jest wytwarzany w statystyce SPSS podczas uruchamiania niezależnej procedury testu T., Jeśli uruchomiłeś Test równości wariancji Levene ' a w statystyce SPSS, otrzymasz wynik podobny do poniższego:

Ten test jednorodności wariancji zawiera statystykę F i wartość istotności (wartość p). Chodzi nam przede wszystkim o wartość istotności-jeśli jest ona większa niż 0.05 (tj. p >.05), nasze wariancje grupowe można traktować jako równe. Jeśli jednak p < 0.05, mamy nierówne wariancje i naruszyliśmy założenie jednorodności wariancji.,
przezwyciężenie naruszenia założenia jednorodności wariancji
Jeśli test Levenego na równość wariancji jest statystycznie istotny, co wskazuje, że wariancje grupowe są nierówne w populacji, można skorygować to naruszenie, nie stosując zbiorczego oszacowania dla terminu błędu dla statystyki t, ale zamiast tego stosując korektę stopni swobody za pomocą metody Welcha-Satterthwaite ' a., W całej rzeczywistości prawdopodobnie nigdy nie słyszałeś o tych korektach, ponieważ statystyki SPSS ukrywają te informacje i po prostu etykietują dwie opcje jako „zakładane równe wariancji” i „równe wariancji nie zakładane”bez wyraźnego określenia użytych testów., Jednakże, możesz zobaczyć dowody tych testów jak poniżej:
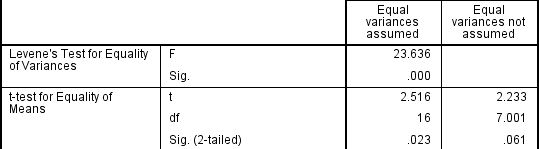
z wyniku testu Levene ' a na równość wariancji, możemy odrzucić hipotezę zerową, że nie ma różnicy w wariancjach między grupami i zaakceptować hipotezę alternatywną, że istnieje statystycznie istotna różnica w wariancjach między grupami., Efekt braku możliwości zakładania równych wariancji jest widoczny w końcowej kolumnie powyższego rysunku, gdzie widzimy zmniejszenie wartości statystyki t i duże zmniejszenie stopni swobody (df). Ma to wpływ na zwiększenie wartości p powyżej poziomu istotności krytycznej 0,05. W tym przypadku nie akceptujemy zatem hipotezy alternatywnej i przyjmujemy, że nie ma statystycznie istotnych różnic między środkami. Nie byłby to nasz wniosek, gdybyśmy nie testowali jednorodności wariancji.