klasycznie myślimy o świetle, jak zawsze poruszającym się po liniach prostych, ale gdy fale świetlne przechodzą w pobliżu bariery, mają tendencję do wyginania się wokół tej bariery i rozprzestrzeniania się. Dyfrakcja światła występuje, gdy fala świetlna przechodzi przez róg lub przez otwór lub szczelinę, która jest fizycznie przybliżoną wielkością lub nawet mniejszą od długości fali tego światła.,

bardzo prostą demonstrację dyfrakcji można przeprowadzić trzymając rękę przed źródłem światła i powoli zamykając dwa palce, obserwując światło przesyłane między nimi. Gdy palce zbliżają się do siebie i zbliżają się bardzo blisko siebie, zaczynasz widzieć serię ciemnych linii równoległych do palców. Linie równoległe są w rzeczywistości wzorcami dyfrakcyjnymi. Zjawisko to może również wystąpić, gdy światło jest „wygięte” wokół cząstek, które znajdują się w tym samym rzędzie wielkości, co długość fali światła., Dobrym tego przykładem jest dyfrakcja światła słonecznego przez chmury, którą często określamy jako srebrną podszewkę, zilustrowaną na rysunku 1 z pięknym zachodem słońca nad oceanem.
często możemy zaobserwować pastelowe odcienie niebieskiego, różu, fioletu i zieleni w chmurach, które powstają, gdy światło jest rozpraszane przez krople wody w chmurach. Ilość dyfrakcji zależy od długości fali światła, przy czym krótsze długości fal są dyfrakowane pod większym kątem niż dłuższe (w efekcie światło niebieskie i fioletowe są dyfrakowane pod większym kątem niż światło czerwone)., Gdy fala świetlna podróżująca przez atmosferę napotka kroplę wody, Jak pokazano poniżej, najpierw załamuje się ona w interfejsie woda:powietrze, a następnie odbija się, gdy ponownie napotka interfejs. Wiązka, wciąż poruszająca się wewnątrz kropli wody, jest ponownie załamana, gdy uderza w interfejs po raz trzeci. Ta ostatnia interakcja z interfejsem załamuje światło z powrotem do atmosfery, ale także rozprasza część światła, jak pokazano poniżej., Ten element dyfrakcyjny prowadzi do zjawiska zwanego halo Celliniego (znanego również jako efekt Heiligenscheina), w którym jasny pierścień światła otacza Cień głowy obserwatora.
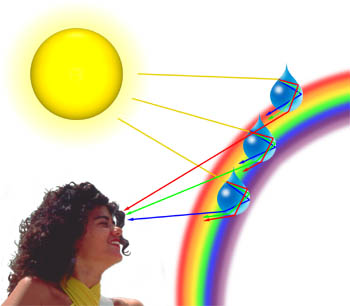
terminy dyfrakcja i rozpraszanie są często używane zamiennie i są uważane za niemal synonimy. Dyfrakcja opisuje wyspecjalizowany przypadek rozpraszania światła, w którym obiekt o regularnie powtarzających się cechach (takich jak kratka dyfrakcyjna) wytwarza uporządkowaną dyfrakcję światła we wzorze dyfrakcyjnym., W świecie rzeczywistym większość obiektów ma bardzo złożone kształty i należy je uważać za złożone z wielu indywidualnych cech dyfrakcyjnych, które mogą wspólnie wytwarzać losowe rozpraszanie światła.
jednym z klasycznych i najbardziej fundamentalnych pojęć dotyczących dyfrakcji jest jednościenny optyczny eksperyment dyfrakcyjny, przeprowadzony po raz pierwszy na początku XIX wieku. Gdy fala świetlna rozchodzi się przez szczelinę (lub aperturę), wynik zależy od fizycznego rozmiaru apertury w odniesieniu do długości fali padającej wiązki., Jest to zilustrowane na rysunku 3 przy założeniu, że spójna, Monochromatyczna fala emitowana ze źródła punktowego S, podobna do światła, które byłoby wytwarzane przez laser, przechodzi przez aperturę d i jest dyfrakowana, przy czym główna padająca wiązka światła ląduje w punkcie P, A Pierwsze wtórne maksimum występuje w punkcie Q.
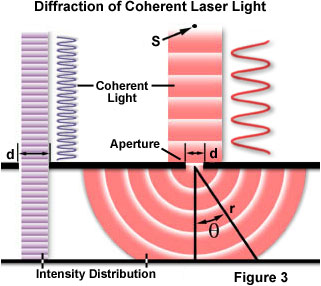
jak pokazano na lewej stronie rysunku, gdy długość fali (λ) jest znacznie mniejsza niż szerokość apertury (d).), fala po prostu porusza się w linii prostej, tak jak gdyby była cząstką lub nie było apertury., Jednak gdy długość fali przekracza rozmiar apertury, doświadczamy dyfrakcji światła zgodnie z równaniem:
gdzie θ jest kątem między padającym centralnym kierunkiem propagacji a pierwszym minimum wzoru dyfrakcyjnego. Eksperyment daje jasne maksimum Centralne, które jest otoczone z obu stron przez maksimum wtórne, przy czym intensywność każdego następnego maksimum wtórnego maleje wraz ze wzrostem odległości od centrum. Rysunek 4 ilustruje ten punkt za pomocą wykresu natężenia wiązki w stosunku do promienia dyfrakcji., Należy zauważyć, że minima występujące pomiędzy maksymami drugorzędnymi znajdują się w wielokrotnościach π.
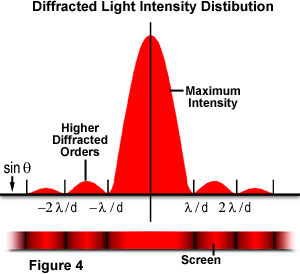
ten eksperyment został po raz pierwszy wyjaśniony przez Augustina Fresnela, który wraz z Thomasem Youngiem dostarczył ważnych dowodów potwierdzających, że światło porusza się w falach. Na powyższych rysunkach widzimy, jak koherentne, monochromatyczne światło (w tym przykładzie oświetlenie laserowe) emitowane z punktu L jest rozpraszane przez aperturę D., Fresnel zakładał, że amplituda Maksima pierwszego rzędu w punkcie Q(zdefiniowanym jako eQ) będzie dana przez równanie:
gdzie A jest amplitudą fali padającej, r jest odległością między d i Q, A F (χ) Jest funkcją χ, współczynnikiem nachylenia wprowadzonym przez Fresnela.
dyfrakcja Światła
zbadaj, jak wiązka światła ulega dyfrakcji, gdy przechodzi przez wąską szczelinę lub aperturę. Dostosuj długość fali i rozmiar przysłony i obserwuj, jak wpływa to na wzór intensywności dyfrakcji.,
dyfrakcja światła odgrywa kluczową rolę w ograniczaniu mocy rozdzielczej dowolnego instrumentu optycznego (na przykład: aparatów fotograficznych, lornetek, teleskopów, mikroskopów i oka). Moc rozdzielcza to zdolność instrumentu optycznego do tworzenia oddzielnych obrazów dwóch sąsiednich punktów. Jest to często określane przez jakość soczewek i luster w przyrządzie, a także właściwości otaczającego medium (Zwykle powietrza). Falowa natura światła wymusza ostateczną granicę mocy rozdzielczej wszystkich instrumentów optycznych.,
nasze dyskusje na temat dyfrakcji wykorzystały szczelinę jako aperturę, przez którą światło jest dyfrakowane. Jednak wszystkie instrumenty optyczne mają okrągłe apertury, na przykład źrenica oka lub okrągła membrana i soczewki mikroskopu. Otwory okrągłe wytwarzają wzory dyfrakcyjne podobne do opisanych powyżej, z tym że wzór naturalnie wykazuje symetrię kołową. Analiza matematyczna wzorów dyfrakcyjnych wytwarzanych przez okrągłą aperturę jest opisana równaniem:
gdzie θ (1) jest położeniem kątowym minima dyfrakcyjnego pierwszego rzędu (pierwszego ciemnego pierścienia), λ jest długością fali padającego światła, d jest średnicą przysłony, a 1,22 jest stałą. W większości przypadków kąt θ(1) jest bardzo mały, więc przybliżenie, że sin I tan kąta są prawie równe daje:
z tych równań wynika, że maksimum centralne jest wprost proporcjonalne do λ/d, co czyni to maksimum bardziej rozłożonym dla dłuższych długości fal i dla mniejszych apertur., Wtórna mimina dyfrakcji wyznacza granicę przydatnego powiększenia soczewek obiektywowych w mikroskopii optycznej, ze względu na wrodzoną dyfrakcję światła przez te soczewki. Bez względu na to, jak doskonały może być obiektyw, obrazowi punktowego źródła światła wytwarzanego przez obiektyw towarzyszy maksimum drugiego i wyższego rzędu. Można to wyeliminować tylko wtedy, gdy obiektyw miał nieskończoną średnicę. Dwa obiekty oddzielone odległością mniejszą niż θ (1) nie mogą być rozwiązane, bez względu na to, jak duża jest moc powiększenia., Podczas gdy te równania zostały wyprowadzone dla obrazu punktowego źródła światła w nieskończonej odległości od apertury, jest to rozsądne przybliżenie mocy rozdzielczej mikroskopu, gdy D zastępuje średnicę soczewki obiektywu.
Tak więc, jeśli dwa obiekty znajdują się w odległości D od siebie i znajdują się w odległości L od obserwatora, kąt (wyrażony w radianach) między nimi wynosi:
, co prowadzi nas do skondensowania dwóch ostatnich równań do uzyskania:
gdzie D(0) jest minimalną odległością między obiektami, która pozwoli na ich rozwiązanie. Używając tego równania, ludzkie oko może rozwiązać obiekty oddzielone od siebie odległością 0,056 milimetra, jednak fotoreceptory w siatkówce nie są wystarczająco blisko siebie, aby umożliwić ten stopień rozdzielczości, a 0,1 milimetra jest bardziej realistyczną liczbą w normalnych warunkach.
o sile rozdzielczej mikroskopów optycznych decyduje wiele czynników, w tym te omówione, ale w najbardziej idealnych okolicznościach liczba ta wynosi około 0,2 mikrometra., Liczba ta musi uwzględniać optyczne ustawienie mikroskopu, jakość soczewek, a także przeważające długości fal światła używane do obrazowania próbki. Chociaż często nie jest konieczne obliczanie dokładnej mocy rozdzielczej każdego obiektywu (i w większości przypadków byłoby to stratą czasu), ważne jest, aby zrozumieć możliwości soczewek mikroskopu, ponieważ mają one zastosowanie w rzeczywistym świecie.
Mortimer Abramowitz – Olympus America, Inc., Two Corporate Center Drive., Melville, New York, 11747.
Michał W., Davidson-National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., Florida State University, Tallahassee, Floryda, 32310.