wprowadzenie
regresja liniowa, znana również jako prosta regresja liniowa lub dwuwymiarowa regresja liniowa, jest używana, gdy chcemy przewidzieć wartość zmiennej zależnej na podstawie wartości zmiennej niezależnej. Na przykład, można użyć regresji liniowej, aby zrozumieć, czy wydajność egzaminu można przewidzieć na podstawie czasu rewizji (tj.,, zmienną zależną będzie „exam performance”, mierzony od 0-100 marks, a zmienną niezależną będzie „revision time”, mierzony w godzinach). Alternatywnie możesz użyć regresji liniowej, aby zrozumieć, czy można przewidzieć zużycie papierosów na podstawie czasu palenia (tj. zmienną zależną będzie „zużycie papierosów”, mierzona w kategoriach liczby papierosów spożywanych dziennie, a zmienną niezależną będzie „czas palenia”, mierzona w dniach). Jeśli masz dwie lub więcej niezależnych zmiennych, a nie tylko jedną, musisz użyć regresji wielokrotnej., Alternatywnie, jeśli chcesz tylko ustalić, czy istnieje zależność liniowa, możesz użyć korelacji Pearsona.
Uwaga: zmienna zależna jest również określana jako zmienna wyniku, celu lub kryterium, podczas gdy zmienna niezależna jest również określana jako zmienna predykcyjna, wyjaśniająca lub regresorowa. Ostatecznie, niezależnie od używanego terminu, najlepiej jest być konsekwentnym. W tym przewodniku będziemy odnosić się do tych zmiennych jako zależnych i niezależnych.,
w tym przewodniku pokażemy, jak przeprowadzić regresję liniową za pomocą Stata, a także zinterpretować i zgłosić wyniki tego testu. Zanim jednak przedstawimy Ci tę procedurę, musisz zrozumieć różne założenia, które muszą spełniać Twoje dane, aby regresja liniowa dała prawidłowy wynik. Następnie omówimy te założenia.
Stata
założenia
istnieje siedem „założeń”, które stanowią podstawę regresji liniowej. Jeśli którykolwiek z tych siedmiu założeń nie jest spełniony, nie można analizować danych za pomocą liniowego, ponieważ nie otrzymasz poprawnego wyniku., Ponieważ założenia #1 i #2 odnoszą się do wybranych zmiennych, nie można ich przetestować pod kątem użycia Stata. Zanim jednak przejdziesz dalej, powinieneś zdecydować, czy Twoje badanie spełnia te założenia.
- założenie #1: zmienna zależna powinna być mierzona na poziomie ciągłym., Przykładami takich zmiennych ciągłych są wysokość (mierzona w stopach i calach), temperatura (mierzona w oC), wynagrodzenie( mierzone w dolarach amerykańskich), czas rewizji (mierzony w godzinach), inteligencja (mierzona przy użyciu wyniku IQ), Czas reakcji (mierzony w milisekundach), wydajność testu (mierzona od 0 do 100), sprzedaż (mierzona w liczbie transakcji miesięcznie) i tak dalej. Jeśli nie masz pewności, czy zmienna zależna jest ciągła (tj. mierzona na poziomie interwału lub współczynnika), zobacz nasz przewodnik typów zmiennych.,
- założenie # 2: twoja zmienna niezależna powinna być mierzona na poziomie ciągłym lub kategorycznym. Jeśli jednak masz kategoryczną zmienną niezależną, bardziej powszechne jest użycie niezależnego testu t (dla 2 grup) lub jednokierunkowego ANOVA(dla 3 grup lub więcej). Jeśli nie masz pewności, przykłady zmiennych kategorycznych obejmują płeć (np. 2 grupy: mężczyzna i kobieta), pochodzenie etniczne( np. 3 grupy: Kaukaska, afroamerykańska i hiszpańska), poziom aktywności fizycznej (np. 4 grupy: siedzący tryb życia, niski, umiarkowany i wysoki) i zawód (np.,, 5 grup: chirurg, lekarz, pielęgniarka, dentysta, terapeuta). W tym przewodniku pokazujemy procedurę regresji liniowej i wyjście Stata, gdy zarówno zmienne zależne, jak i niezależne były mierzone na poziomie ciągłym.
na szczęście można sprawdzić założenia #3, #4, #5, #6 i # 7 przy użyciu Stata. Przechodząc do założeń #3, #4, #5, #6 i # 7, sugerujemy przetestowanie ich w tej kolejności, ponieważ reprezentuje kolejność, w której, jeśli naruszenie założenia nie jest poprawne, nie będzie już w stanie korzystać z regresji liniowej., W rzeczywistości, nie zdziw się, jeśli dane nie jeden lub więcej z tych założeń, ponieważ jest to dość typowe podczas pracy z danymi w świecie rzeczywistym, a nie podręcznikowych przykładów, które często tylko pokazać, jak przeprowadzić regresję liniową, gdy wszystko idzie dobrze. Nie martw się jednak, ponieważ nawet jeśli Twoje dane zawiodą pewne założenia, często istnieje rozwiązanie, które może je przezwyciężyć (np. przekształcenie danych lub użycie innego testu statystycznego)., Pamiętaj tylko, że jeśli nie sprawdzisz, czy dane spełniają te założenia lub przetestujesz je nieprawidłowo, wyniki uzyskane podczas uruchamiania regresji liniowej mogą nie być poprawne.
- założenie #3: musi istnieć zależność liniowa między zmiennymi zależnymi i niezależnymi. Chociaż istnieje wiele sposobów, aby sprawdzić, czy istnieje zależność liniowa między dwiema zmiennymi, sugerujemy utworzenie plotera rozpraszającego za pomocą Stata, gdzie można wykreślić zmienną zależną z zmienną niezależną., Następnie możesz obejrzeć wykres punktowy, aby sprawdzić liniowość. Twój scatterplot może wyglądać mniej więcej tak:
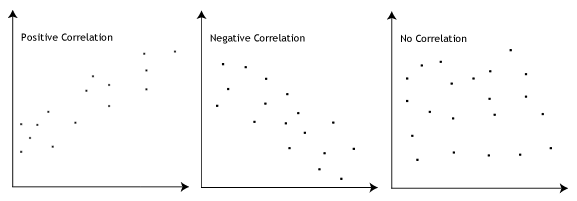
jeśli relacja wyświetlana w Twoim scatterplot nie jest liniowa, będziesz musiał przeprowadzić nieliniową analizę regresji lub „przekształcić” Twoje dane, co możesz zrobić za pomocą Stata.
- założenie # 4: nie powinno być znaczących odstających wartości. Wartości odstające są po prostu pojedynczymi punktami danych w danych, które nie odpowiadają zwykłemu wzorcowi (np.,, w badaniu z wynikiem IQ 100 uczniów, gdzie średni wynik wynosił 108 z niewielką różnicą między uczniami, jeden uczeń miał wynik 156, co jest bardzo nietypowe, a nawet może umieścić ją w 1% najlepszych wyników IQ na świecie). Następujące punkty rozpraszające podkreślają potencjalny wpływ wartości odstających:
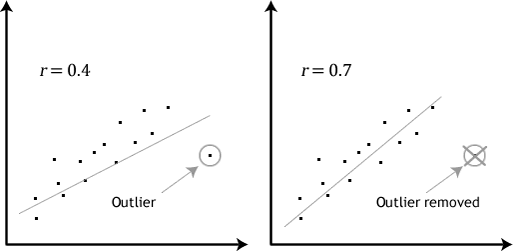
problem z wartościami odstającymi polega na tym, że mogą mieć negatywny wpływ na równanie regresji, które jest używane do przewidywania wartości zmiennej zależnej na podstawie zmiennej niezależnej., Spowoduje to zmianę wyników generowanych przez Stata i zmniejszy predykcyjną dokładność wyników. Na szczęście można użyć Stata do przeprowadzenia diagnostyki casewise, aby pomóc wykryć możliwe wartości odstające.
- założenie # 5: powinieneś mieć niezależność obserwacji, którą możesz łatwo sprawdzić za pomocą statystyki Durbina-Watsona, która jest prostym testem do uruchomienia przy użyciu staty.
- założenie # 6: Twoje dane muszą pokazywać homoscedastyczność, czyli gdzie wariancje wzdłuż linii najlepszego dopasowania pozostają podobne, gdy poruszasz się wzdłuż linii., Poniższe dwa punkty rozrzutu zawierają proste przykłady danych, które spełniają to założenie i które nie spełniają tego założenia:
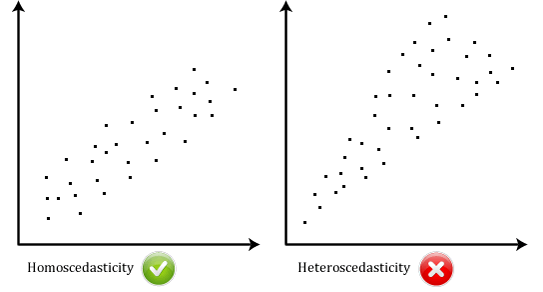
kiedy analizujesz własne dane, będziesz miał szczęście, jeśli twój punkt rozrzutu wygląda jak jeden z dwóch powyższych. Chociaż pomagają one zilustrować różnice w danych, które spełniają lub naruszają założenie homoscedasticity, rzeczywiste dane są często o wiele bardziej bałagan., Możesz sprawdzić, czy Twoje dane wykazały homoscedasticity poprzez wykreślenie regresji znormalizowanych pozostałości przed regresji znormalizowanej wartości przewidywanej.
- założenie # 7: na koniec należy sprawdzić, czy pozostałości (błędy) linii regresji są w przybliżeniu rozkładane normalnie. Dwie popularne metody sprawdzania tego założenia obejmują wykorzystanie histogramu (z nałożoną krzywą normalną)lub normalnego wykresu P-P.
w praktyce sprawdzanie założeń #3, #4, #5, #6 i #7 prawdopodobnie zajmie większość czasu podczas przeprowadzania regresji liniowej., Jednak nie jest to trudne zadanie, a Stata zapewnia wszystkie narzędzia, których potrzebujesz, aby to zrobić.
w sekcji procedura przedstawiamy procedurę Stata wymaganą do wykonania regresji liniowej przy założeniu, że żadne założenia nie zostały naruszone. Najpierw przedstawiamy przykład, którego używamy do wyjaśnienia procedury regresji liniowej w Stata.
przykład
przykład
badania pokazują, że ćwiczenia mogą pomóc w zapobieganiu chorobom serca. W rozsądnych granicach, im więcej ćwiczysz, tym mniejsze ryzyko wystąpienia chorób serca., Jednym ze sposobów, w jaki ćwiczenia zmniejszają ryzyko wystąpienia chorób serca, jest redukcja tłuszczu we krwi, zwanego cholesterolem. Im więcej ćwiczysz, tym niższe stężenie cholesterolu. Ponadto niedawno wykazano, że ilość czasu spędzanego na oglądaniu telewizji-wskaźnik siedzącego trybu życia-może być dobrym wskaźnikiem chorób serca (to znaczy, że im więcej oglądasz telewizji, tym większe ryzyko chorób serca).,
dlatego badacz postanowił ustalić, czy stężenie cholesterolu jest związane z czasem spędzonym na oglądaniu telewizji u zdrowych mężczyzn w wieku 45-65 lat (kategoria osób zagrożonych). Na przykład, gdy ludzie spędzali więcej czasu na oglądaniu telewizji, czy ich stężenie cholesterolu również wzrosło (pozytywny związek); czy stało się odwrotnie? Badacz chciał również poznać proporcję stężenia cholesterolu, którą może wyjaśnić czas spędzony na oglądaniu telewizji, a także możliwość przewidywania stężenia cholesterolu., Badacz mógł wtedy ustalić, czy na przykład osoby, które spędzały osiem godzin na oglądanie telewizji dziennie, miały niebezpiecznie wysoki poziom cholesterolu w porównaniu do osób oglądających tylko dwie godziny telewizji.
aby przeprowadzić analizę, badacz zwerbował 100 zdrowych mężczyzn w wieku od 45 do 65 lat. Ilość czasu spędzonego na oglądaniu telewizji (tj. zmienna niezależna, time_tv) i stężenie cholesterolu (tj. zmienna zależna, cholesterol) zostały zarejestrowane dla wszystkich 100 uczestników., Wyrażona w kategoriach zmiennych, badacz chciał regresji cholesterolu na czas_tv.
Uwaga: przykład i dane użyte w tym przewodniku są fikcyjne. Stworzyliśmy je właśnie na potrzeby tego przewodnika.
Stata
Konfiguracja w Stata
uwaga: nie ma znaczenia, czy najpierw utworzysz zmienną zależną czy niezależną.
Po utworzeniu tych dwóch zmiennych-time_tv i cholesterol – wprowadziliśmy wyniki dla każdej z nich do dwóch kolumn edytora danych (Edit) arkusza kalkulacyjnego (tj.,, czas w godzinach, w których uczestnicy oglądali telewizję w lewej kolumnie (tj. time_tv, zmienna niezależna) oraz stężenie cholesterolu w mmol/L w prawej kolumnie (tj. cholesterol, zmienna zależna), jak pokazano poniżej:
opublikowane za pisemną zgodą StataCorp LP.,
Stata
procedura testowa w Stata
w tej sekcji pokazujemy, jak analizować dane za pomocą regresji liniowej w Stata, gdy sześć założeń w poprzedniej sekcji, założenia, nie zostały naruszone. Możesz przeprowadzić regresję liniową za pomocą kodu lub graficznego interfejsu użytkownika Stata (GUI). Po przeprowadzeniu analizy pokażemy Ci, jak interpretować wyniki. Najpierw wybierz, czy chcesz używać kodu, czy graficznego interfejsu użytkownika (GUI) staty.,
Kod
kod do przeprowadzenia regresji liniowej na danych ma postać:
regress DependentVariable IndependentVariable
Ten kod jest wprowadzany do pole poniżej:
opublikowane za pisemną zgodą statacorp LP.,
używając naszego przykładu, gdzie zmienną zależną jest cholesterol, a zmienną niezależną jest time_tv, wymagany kod będzie:
regress cholesterol time_tv
Uwaga 1: Musisz być precyzyjny podczas wprowadzania kodu do pola . W kodzie jest rozróżniana wielkość liter. Na przykład, jeśli wpisałeś „Cholesterol”, gdzie „C” jest wielką literą, a nie małą literą (tj.,, małe „c”), które powinno być, otrzymasz komunikat o błędzie w następujący sposób:
Uwaga 2: jeśli nadal otrzymujesz komunikat o błędzie w uwadze 2: powyżej, warto sprawdzić nazwę podaną przez dwie zmienne w edytorze danych podczas konfigurowania pliku (np. zobacz ekran edytora danych powyżej)., W polu po prawej stronie ekranu edytora danych, jest to sposób, w jaki zapisujesz swoje zmienne w sekcji
, a nie w sekcji
, którą musisz wprowadzić do kodu (patrz poniżej nasza zmienna zależna). Może to wydawać się oczywiste, ale czasami popełniany jest błąd, co prowadzi do błędu w uwadze 2 powyżej.
dlatego wprowadź kod, Cofnij time_tv i naciśnij przycisk „Return / Enter” na klawiaturze.,
opublikowane za pisemną zgodą StataCorp LP.
możesz zobaczyć wyjście Stata, które zostanie wyprodukowane tutaj.,
graficzny interfejs użytkownika (GUI)
trzy kroki wymagane do przeprowadzenia regresji liniowej w Stata 12 i 13 są pokazane poniżej:
- kliknij statystyki > Modele liniowe i powiązane > regresja liniowa w menu głównym, jak pokazano poniżej: > 7922cf473c”>
opublikowane za pisemną zgodą statacorp LP.,
zostanie wyświetlone okno dialogowe regres-regresja liniowa:
opublikowane za pisemną zgodą StataCorp LP.
- Wybierz z listy rozwijanej zmienna zależna:, a time_tv z listy rozwijanej zmienne niezależne:. Zostanie wyświetlony następujący ekran:
opublikowany za pisemną zgodą StataCorp LP.,
-
kliknij przycisk
. To wygeneruje wyjście.
Stata
wyjście analizy regresji liniowej w Stata
Jeśli Twoje dane przeszły założenie #3 (tzn. nie było liniowej zależności między twoimi dwiema zmiennymi), #4 (tzn. nie było znaczących wartości odstających), założenie #5 (tzn. miałeś niezależność obserwacji), założenie # 6 (tzn. Twoje dane wykazały homoscedasticity) i założenie #7 (tzn.,, pozostałości (błędy) były w przybliżeniu rozkładane normalnie), co wyjaśniliśmy wcześniej w sekcji założenia, wystarczy zinterpretować następujące wyjście regresji liniowej w Stacie:
opublikowane za pisemną zgodą StataCorp LP.,
wyjście składa się z czterech ważnych fragmentów informacji: (a) wartość R2 („R-kwadrat” wiersz) reprezentuje proporcję wariancji w zmiennej zależnej, które mogą być wyjaśnione przez naszą zmienną niezależną (technicznie jest to proporcja zmienności rozliczane przez model regresji powyżej i poza modelem średniej). Jednak R2 opiera się na próbie i jest pozytywnie tendencyjnym estymatorem proporcji wariancji zmiennej zależnej uwzględnionej w modelu regresji (tj.,, jest zbyt duża); (b) skorygowana wartość R2 (wiersz”Adj R-kwadrat”), która koryguje dodatnie odchylenie, aby zapewnić wartość oczekiwaną w populacji; (c) Wartość F, stopnie swobody („F( 1, 98)”) i znaczenie statystyczne modelu regresji („Prob > f” wiersz); oraz (d) współczynniki dla stałej i niezależnej zmiennej („Coef.”kolumna), czyli informacje potrzebne do przewidzenia zmiennej zależnej, za pomocą zmiennej niezależnej, time_tv.
w tym przykładzie R2 = 0.151. Skorygowany R2 = 0,143 (do 3 d.p.,), co oznacza, że zmienna niezależna, time_tv, wyjaśnia 14,3% zmienności zmiennej zależnej, cholesterolu, w populacji. Skorygowany R2 jest również oszacowaniem wielkości efektu, który przy 0,143 (14,3%) wskazuje na średnią wielkość efektu, zgodnie z klasyfikacją Cohena (1988). Jednak zwykle jest to R2, a nie skorygowany R2, który jest zgłaszany w wynikach. W tym przykładzie model regresji jest statystycznie istotny, F (1, 98) = 17,47, p = .0001., Oznacza to, że ogólnie zastosowany model może statystycznie znacząco przewidzieć zmienną zależną, cholesterol.
Uwaga: poniżej przedstawiamy wyniki analizy regresji liniowej. Ponieważ jednak powinieneś przetestować swoje dane pod kątem założeń, które wyjaśniliśmy wcześniej w sekcji założenia, musisz również zinterpretować wyjście Stata, które zostało wyprodukowane podczas testowania tych założeń. Obejmuje to: (a) rozrzuty używane do sprawdzenia, czy istnieje liniowa zależność między dwoma zmiennymi (tj., Założenie #4); (c) wyjście ze statystyki Durbin-Watson w celu sprawdzenia niezależności obserwacji (tj. założenie #5); (d) punkt rozrzutu regresji standaryzowanych pozostałości w stosunku do regresji standaryzowanej przewidywanej wartości w celu określenia, czy dane wykazały homoscedasticity (tj. założenie #6); i histogram (z nałożoną krzywą normalną) i normalny Wykres P-P w celu sprawdzenia, czy dane wykazały homoscedastyczność (tj. założenie #6); i histogram (z nałożoną krzywą normalną) i normalny Wykres P-P w celu sprawdzenia, czy pozostałości (błędy) były w przybliżeniu normalnie rozłożone (tj. założenie #7)., Ponadto, należy pamiętać, że jeśli dane nie którykolwiek z tych założeń, wyjście, które można uzyskać z procedury regresji liniowej (to znaczy, wyjście omawiamy powyżej) nie będzie już istotne, i może trzeba przeprowadzić inny test statystyczny do analizy danych.,
Stata
raportowanie wyników analizy regresji liniowej
podczas raportowania wyników analizy regresji liniowej dobrą praktyką jest uwzględnienie: a) wprowadzenia do przeprowadzonej analizy; b) informacji o próbce, w tym wszelkich brakujących wartości; c) obserwowanej wartości F, stopni swobody i poziomu istotności (tj. wartości p); d) procent zmienności zmiennej zależnej wyjaśnionej przez zmienną niezależną (tj. twoje skorygowane R2 ); oraz (E) równanie regresji dla Twojego modelu., Na podstawie powyższych wyników możemy przedstawić wyniki tego badania w następujący sposób:
- ogólne
regresja liniowa ustaliła, że dzienny czas spędzony na oglądaniu telewizji może statystycznie znacząco przewidzieć stężenie cholesterolu, F(1, 98) = 17,47, p = .0001 i czas spędzony na oglądaniu telewizji stanowiły 14,3% wyjaśnionej zmienności stężenia cholesterolu. Równanie regresji było następujące: przewidywane stężenie cholesterolu = -2,135 + 0,044 x (czas spędzony na oglądaniu telewizji).,
oprócz raportowania wyników jak powyżej, można użyć diagramu do wizualnej prezentacji wyników. Na przykład, można to zrobić za pomocą scatterplot z ufnością i przedziałami przewidywania(chociaż nie jest to bardzo powszechne, aby dodać ostatni). Może to ułatwić innym zrozumienie Twoich wyników. Ponadto, możesz użyć równania regresji liniowej do przewidywania wartości zmiennej zależnej na podstawie różnych wartości zmiennej niezależnej., Chociaż Stata nie generuje tych wartości w ramach powyższej procedury regresji liniowej, w Stacie istnieje procedura, której możesz użyć do tego celu.