efekty uczenia się
- Zidentyfikuj ogniska, wierzchołki, osie i środek elipsy.
- napisz równania elipsy wyśrodkowane na początku.
- napisz równania elipsy nie wyśrodkowane na początku.
sekcja stożkowa lub stożkowa jest kształtem wynikającym z przecięcia prawego stożka okrągłego z płaszczyzną. Kąt, pod jakim płaszczyzna przecina stożek, decyduje o kształcie.,
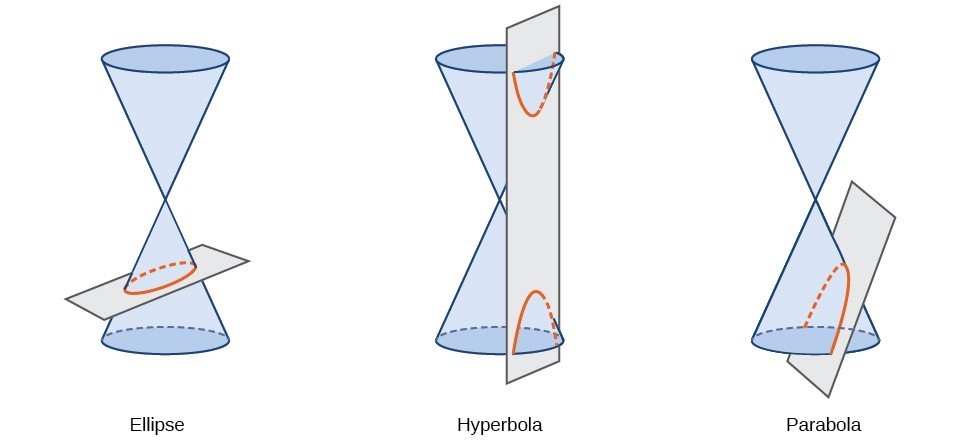
sekcje stożkowe mogą być również opisane za pomocą zbioru punktów na płaszczyźnie współrzędnych. W dalszej części tego rozdziału zobaczymy, że wykres dowolnego równania kwadratowego w dwóch zmiennych jest sekcją stożkową. Znaki równań i współczynniki zmiennych określają kształt. Ta sekcja skupia się na czterech wariantach standardowej postaci równania dla elipsy. Elipsa jest zbiorem wszystkich punktów \ left (x, y \ right)na płaszczyźnie takiej, że suma ich odległości od dwóch stałych punktów jest stała., Każdy punkt stały nazywany jest ogniskiem (w liczbie mnogiej: ogniskiem) elipsy.
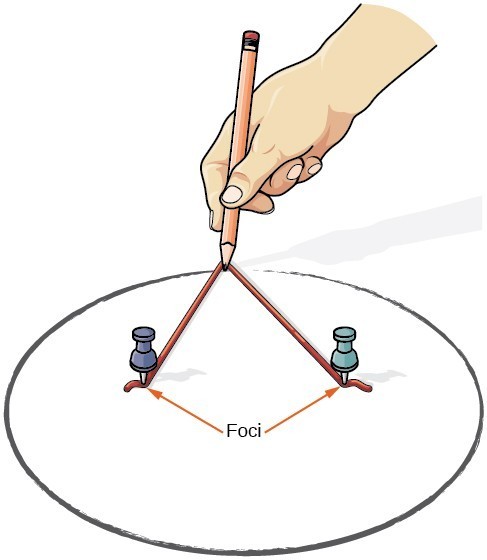
możemy narysować elipsę za pomocą kawałka kartonu, dwóch pinezek, ołówka i sznurka. Umieść kciuki w kartonie, aby utworzyć ogniska elipsy. Wytnij kawałek sznurka dłuższego niż odległość między dwoma pinezkami (długość sznurka reprezentuje stałą w definicji). Przypnij każdy koniec sznurka do kartonu i wyznacz krzywą za pomocą ołówka napiętego do sznurka. Rezultatem jest elipsa.
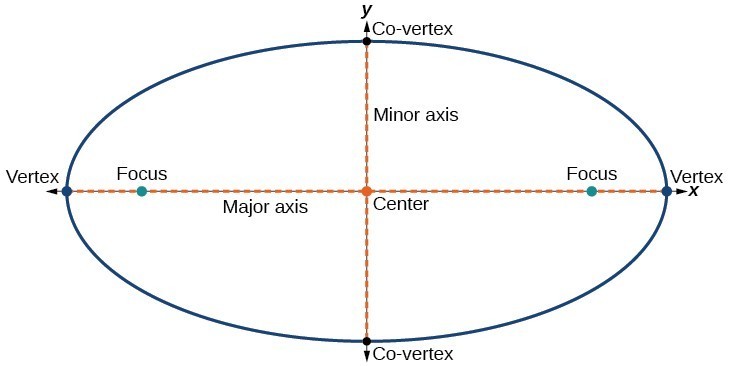
każda elipsa ma dwie osie symetrii., Dłuższa oś nazywana jest główną osią, a krótsza oś nazywana jest małą osią. Każdy punkt końcowy osi głównej jest wierzchołkiem elipsy (liczba mnoga: wierzchołki), a każdy punkt końcowy osi podrzędnej jest wierzchołkiem równoległym elipsy. Środek elipsy jest punktem środkowym osi głównej i małej. Osie są prostopadłe w centrum. Ogniska zawsze leżą na głównej osi, a suma odległości od ognisk do dowolnego punktu na elipsie (suma stała) jest większa niż odległość między ogniskami.,
w tej sekcji ograniczamy elipsy do tych, które są umieszczone pionowo lub poziomo w płaszczyźnie współrzędnych. Oznacza to, że osie będą leżeć na osiach x i y lub będą równoległe do nich. W dalszej części rozdziału zobaczymy elipsy, które są obracane w płaszczyźnie współrzędnych.
aby pracować z poziomymi i pionowymi elipsami na płaszczyźnie współrzędnych, rozważamy dwa przypadki: te, które są wyśrodkowane na początku i te, które są wyśrodkowane w punkcie innym niż początek., Najpierw nauczymy się wyprowadzać równania elipsy, a następnie nauczymy się pisać równania elipsy w standardowej formie. Później użyjemy tego, czego się nauczymy, aby narysować wykresy.,v>Jeśli (x,y) jest punktem na elipsie, to możemy zdefiniować następujące zmienne:
\begin{align}d_1&=\text{odległość od } (-c,0) \text{ do } (x,y) \\ d_2iv id=”dca164596c”
= \text{odległość od } (C,0) \text{ do } (X,Y) \end{align}
\dfrac{x^2}{a^2}+\dfrac{y^2}{B^2}=1
dla elipsy wyśrodkowanej na początku z główną osią na osi X i
\dfrac{X^2}{B^2}+\dfrac{y^2}{a^2}=1
dla elipsy wyśrodkowanej na początku z główną osią na osi Y.,
pisanie równań elipsy Nieośrodkowanej na początku
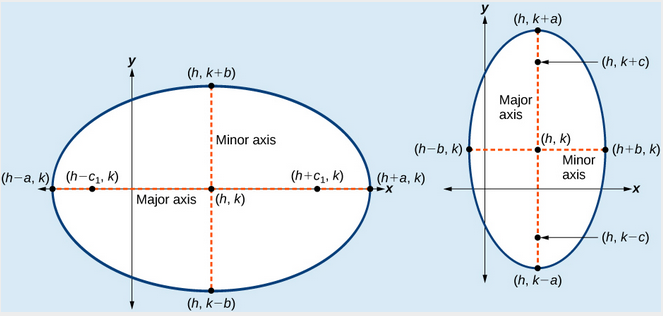
(a) elipsa pozioma ze środkiem w lewo(h,K \right) (b) elipsa pionowa ze środkiem w lewo(h,k\right)
Rozwiązywanie problemów związanych z elipsą
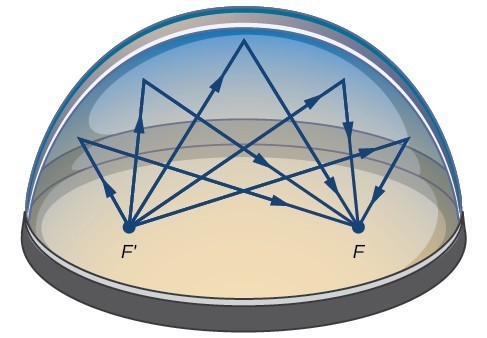
wiele rzeczywistych sytuacji może być reprezentowanych przez elipsy, w tym orbity planet, satelitów, księżyców i komet, a także kształty kilów łodzi, sterów i niektórych skrzydeł samolotu. Urządzenie medyczne zwane litotrypterem wykorzystuje reflektory eliptyczne do rozbijania kamieni nerkowych poprzez generowanie fal dźwiękowych., Niektóre budynki, zwane szeptanymi komnatami, są zaprojektowane z eliptycznymi kopułami, tak aby osoba szepcząca na jednym ognisku mogła być łatwo słyszalna przez kogoś stojącego na drugim ognisku. Dzieje się tak ze względu na właściwości akustyczne elipsy. Gdy fala dźwiękowa powstaje w jednym ognisku Komory szeptanej, fala dźwiękowa odbija się od eliptycznej kopuły i z powrotem do drugiego ogniska. W komnacie szeptów w Muzeum Nauki i przemysłu w Chicago dwie osoby stojące przy ogniskach—oddalone od siebie o około 43 metry-mogą słyszeć szepty.