Een van de grootste aspecten van Sudoku is dat het spel boeiende uitdagingen biedt aan zowel de beginnende als de doorgewinterde puzzelspeler. Wanneer ze een puzzel spelen die is afgestemd op hun competentieniveau, zullen zowel de beginner als de ervaren Sudoku-oplosser een goede hoeveelheid gedachte en techniek moeten steken in het voltooien van de taak. Hun aanpak is echter misschien niet hetzelfde. Het oplossen van een harde Sudoku puzzel vereist een heel andere set van technieken in vergelijking met een eenvoudige., Dit artikel presenteert negen van dergelijke technieken; in toenemende moeilijkheden.
bij het gebruik van deze technieken, de manier waarop de pro ‘ s het liever doen, is om te beginnen met de basis technieken. Gebruik de eerste paar technieken om zoveel mogelijk getallen in te voegen. Als je dan geen nummers meer kunt toevoegen aan het bord met behulp van de basistechnieken, probeer dan de meer geavanceerde. Doe een voor een totdat je nog een getal in een cel kunt plotten. Begin dan opnieuw met de basistechnieken en herhaal het proces. Je moet in staat zijn om bijna elke Sudoku puzzel met behulp van deze technieken op te lossen.,
technieken voor het verwijderen van getallen:
enige kandidaat
Wanneer een specifieke cel slechts een enkel getal kan bevatten, is dat getal een “enige kandidaat”. Dit gebeurt wanneer alle andere nummers, maar het kandidaatnummer bestaat in het huidige blok, kolom of rij. In dit voorbeeld kan de rode cel alleen het nummer 5 bevatten, omdat de andere acht getallen allemaal zijn gebruikt in het gerelateerde blok, kolom en rij.,
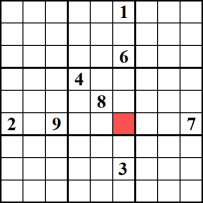
unieke kandidaat
u weet dat elk blok, rij en kolom op een Sudoku-bord elk nummer tussen 1 en 9 moet bevatten. Daarom, als een getal, zeg 4, alleen in een enkele cel binnen een blok/kolom/rij kan worden gezet, dan past dat getal gegarandeerd daar. Dit voorbeeld illustreert het nummer 4 als de unieke kandidaat voor de in rood gemarkeerde cel.,
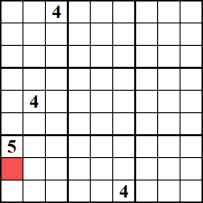
technieken voor het verwijderen van kandidaten:
blok-en kolom / Rijinteractie
Deze methode zal u niet helpen nieuwe getallen in te schrijven, maar het zal u helpen een getal binnen een specifieke rij vast te leggen of Colonne. Het voorbeeld laat zien dat het getal 7 alleen kan worden ingevoegd in de rode cellen van de middelste rij. Zo kunt u 7 als mogelijke kandidaat uit de rest van de rij verwijderen.,
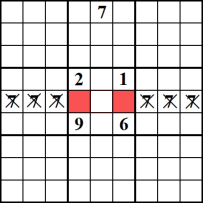
blok / Blokinteractie
Deze techniek wordt het best begrepen door naar het voorbeeld te kijken. In de middelste en de middelste linkerblokken moet het getal 8 in een van de rode cellen worden geplaatst. Dit betekent dat we 8 kunnen elimineren uit de bovenste en onderste rijen in de kolom rechts in het midden.,
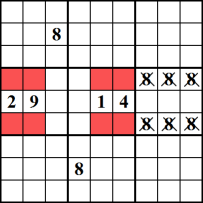
naakte Subset
het voorbeeld laat zien dat Rij nummer 1 en rij nummer 5 beide een cel in dezelfde kolom hebben die alleen de kandidaatnummers 4 en 7 bevat. Deze twee nummers verschijnen ook als kandidaten in alle andere open cellen in die kolom, maar omdat ze de enige twee kandidaten zijn in rijen 1 en 5, kunnen deze twee nummers nergens anders in de rij verschijnen, dus u kunt ze verwijderen. In het voorbeeld zijn de twee in het rood omcirkelde kandidaatparen de enige kandidaten., Aangezien 4 en 7 in een van deze twee cellen moeten worden geplaatst, kunnen alle paren die in blauw zijn omcirkeld, deze getallen als kandidaten verwijderen. In deze puzzel betekent dit 1 wordt enige kandidaat in de tweede rij; 2 wordt enige kandidaat in rij 6; en dus, 6 is enige kandidaat voor rij nummer 4.
U kunt deze techniek ook gebruiken als u meer dan twee kandidaten hebt. Bijvoorbeeld, laten we zeggen dat de paren omcirkeld in rood waren in plaats daarvan drievoudige kandidaten van de nummers 1, 4, 7. Dit zou betekenen dat deze drie nummers in rijen 1, 2 of 5 moeten worden geplaatst., We kunnen deze drie nummers als kandidaten verwijderen in een van de resterende cellen in de kolom. Deze techniek werkt zelfs met vier kandidaatnummers, ervan uitgaande dat u 4 mogelijke kandidaten in vier verschillende cellen in een rij/kolom hebt.
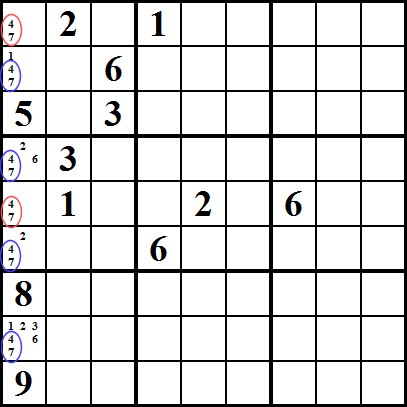
verborgen subset
Dit is vergelijkbaar met naakte subset, maar het beïnvloedt de cellen die de kandidaten bevatten., In dit voorbeeld zien we dat de nummers 5, 6, 7 alleen in cellen 5 of 6 in de eerste kolom kunnen worden geplaatst (gemarkeerd in een rode cirkel), en dat het nummer 5 alleen kan worden ingevoegd in cel nummer 8 (gemarkeerd in een blauwe cirkel). Aangezien 6 en 7 in een van de cellen met een rode cirkel moeten worden geplaatst, volgt hieruit dat het nummer 5 in cel nummer 8 moet worden geplaatst, en dus kunnen we alle andere kandidaten uit de 8ste cel verwijderen; in dit geval, 2 en 3.,
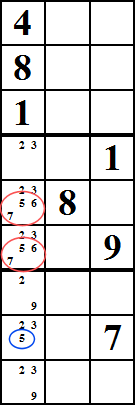
X-Wing
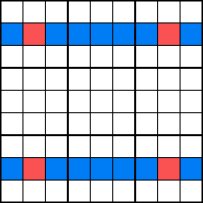
Deze methode kan werken wanneer u kijkt naar cellen die een rechthoek bevatten, zoals de cellen die in het rood zijn gemarkeerd. Laten we in dit voorbeeld zeggen dat de rode en blauwe cellen allemaal het nummer 5 hebben als kandidaatnummers. Stel je nu voor dat de rode cellen de enige cellen zijn in kolom 2 en 8 waarin je 5 kunt plaatsen.
In dit geval moet je natuurlijk een 5 in twee van de rode cellen zetten, en je weet ook dat ze niet beide in dezelfde rij kunnen staan., Dit betekent dat je 5 kunt elimineren als kandidaat voor alle blauwe cellen. Dit komt omdat in de bovenste rij, ofwel de eerste of de tweede rode cel een 5 moet hebben, en hetzelfde kan worden gezegd over de onderste rij.
Swordfish
Swordfish is een meer gecompliceerde versie van X-Wing. In de meeste gevallen, de techniek lijkt misschien veel werk voor zeer weinig loon, maar sommige puzzels kunnen alleen worden opgelost met het. Dus als je een sudoku-oplossende meester wilt zijn, lees dan verder!,
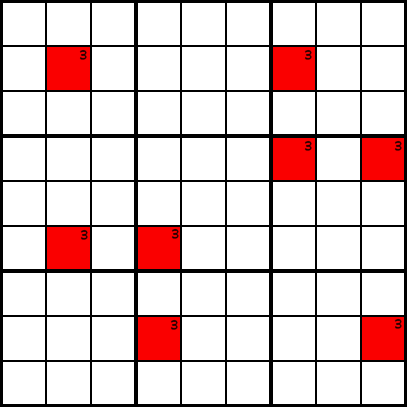Voorbeeld aIn voorbeeld A hebben we in enkele kandidaatcellen voor het getal 3 geplot. Neem nu aan dat in kolom 2, 4, 7 en 9, de enige cellen die het nummer 3 kunnen bevatten, die zijn gemarkeerd in rood. Je weet dat elke kolom een 3 moet bevatten.
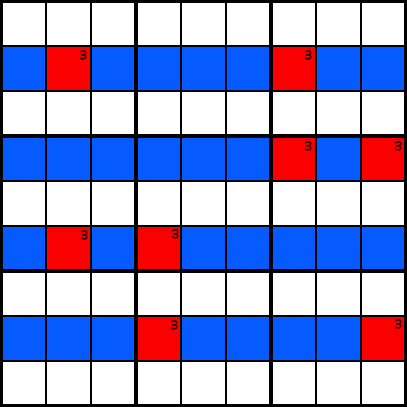voorbeeld bKijk naar voorbeeld B. We kunnen 3 als kandidaat elimineren in elke blauw gemarkeerde cel., De reden hiervoor is dat als we kijken naar de mogelijke plaatsingen van het getal 3 in de rode cellen, we twee alternatieven krijgen: ofwel moet je 3s in de groene cellen, of in de paarse cellen, zoals voorbeeld C laat zien. In ieder geval moet elk van de kolommen 2, 4, 7 en 9 een 3 bevatten in een van de gekleurde cellen, zodat geen enkele andere cel in die rijen een 3 kan bevatten.
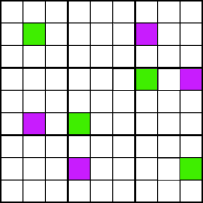voorbeeld CHoe herkent u een swordfish patroon? Je zoekt naar cellen met gemeenschappelijke kandidaatnummers die aan elkaar geketend kunnen worden, zoals in voorbeeld D., Als je begint met de rode cel linksboven. Vervolgens teken je een lijn verticaal of horizontaal totdat je een andere cel bereikt met hetzelfde kandidaatnummer. Vervolgens herhaal je dit patroon totdat je terugkeert naar de oorspronkelijke cel. Als je de originele cel bereikt, heb je een zwaardvis patroon!
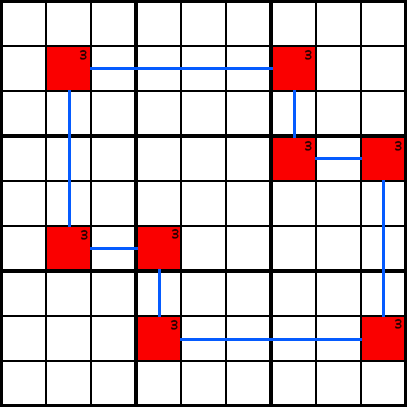voorbeeld DForcing Chain
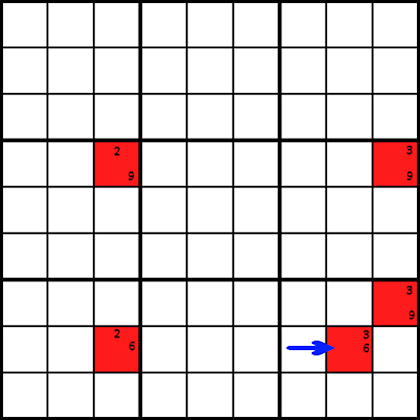
Forcing chain kan u helpen precies te bepalen welk nummer een bepaalde cel moet bevatten. Helaas, de techniek is niet de makkelijkste te gebruiken., Kijk naar het voorbeeld hieronder. Laten we aannemen dat de kandidaten in de rode cellen de enige kandidaten voor die cellen zijn.
Forcing chains werken op de volgende manier: begin met de rode cel met de pijl die ernaar wijst, en vul een van de twee kandidaten in, 3 of 6, voor die cel. Volg daarna op en vul de rest van de rode bloedcellen in. Noteer nu de waarden die u onderweg invoert. Ga terug naar de cel waarmee je begon en probeer het andere kandidaatnummer voor die cel, en vul ook de andere rode cellen in. Vergelijk de cijfers die je nu hebt met het eerste resultaat., U kunt merken dat in beide gevallen een bepaalde cel een specifiek nummer moet bevatten.
In dit voorbeeld, als je het nummer 3 in de startcel plaatst, zul je zien dat de aangrenzende cel boven rechts een 9 moet bevatten. Probeer nu in plaats daarvan een 6 in de startcel in te voeren en beweeg andersom door kandidaatwaarden in te voeren. Wanneer u de boven-rechts naburige cel weer te bereiken, zult u merken dat het moet bevatten een 9 Deze keer rond ook. Deze cel moet dus een 9 bevatten.
dat is het., Hoop dat dit zal u helpen kraken zelfs de moeilijkste sudoku puzzels die er zijn. Succes!
dit artikel is een onderdeel van onze Sudoku Help sectie.
Speel Sudoku Epic
Sudoku Epic is een gratis Sudoku spel van topkwaliteit en is beschikbaar op de meeste platforms: PC, Mac, iPhone, iPad, Android, Google Play Store en Amazon Appstore.
Sudoku Epic op Google Play
Sudoku Epic op iPhone / iPad