berekenen van de oppervlakte onder een curve.
bepaalde integralen
tot nu toe is er bij integratie altijd een constante term over. Om deze reden staan dergelijke integralen bekend als onbepaalde integralen. Bij bepaalde integralen integreren we een functie tussen 2 punten, zodat we de precieze waarde van de integraal kunnen vinden en er geen onbekende constante termen nodig zijn .,

het gebied onder een Curve
het gebied onder een curve tussen twee punten kan worden gevonden door een bepaalde integraal tussen de twee punten te maken.
om het gebied onder de curve y = f(x) tussen x = A en x = b te vinden, integreer y = f(x) tussen de grenzen van a en b.
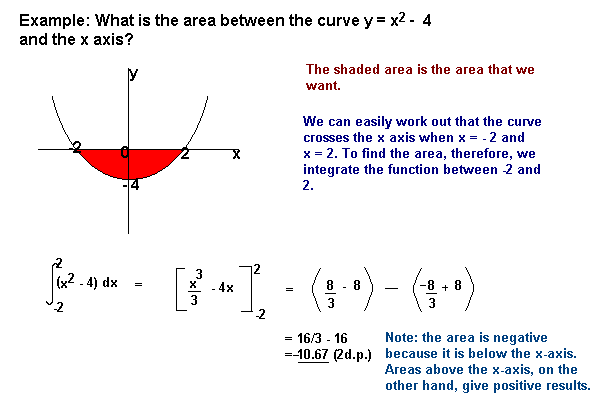
gebieden onder de x-as zullen negatief zijn en gebieden boven de x-as zullen positief zijn. Dit betekent dat je voorzichtig moet zijn bij het vinden van een gebied dat deels boven en deels onder de x-as ligt.,
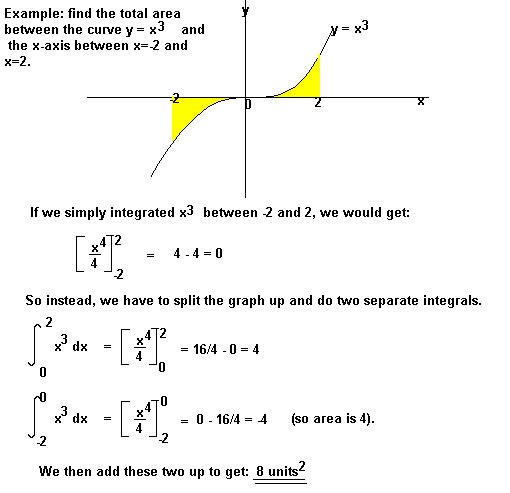
u kunt ook gevraagd worden om het gebied tussen de kromme en de y-as te vinden. Om dit te doen, integreer met betrekking tot y.
voorbeeld
zoek het gebied begrensd door de lijnen y = 0, y = 1 en y = x2.