- beschrijven de basiselementen van een individuele onderzoeksopzet.
- ontwerp enkelvoudige onderzoeken met omkering en meervoudige basislijnontwerpen.
- leg uit hoe individuele onderzoeksontwerpen het probleem van interne validiteit aanpakken.
- interpreteer de resultaten van eenvoudige individuele onderzoeken op basis van de visuele inspectie van grafische gegevens.,
alvorens te kijken naar specifieke individuele onderzoeksontwerpen, zal het nuttig zijn om enkele kenmerken te overwegen die voor de meeste van hen gebruikelijk zijn. Veel van deze kenmerken worden geïllustreerd in Figuur 10.2, die de resultaten van een algemene studie van één onderwerp toont. Ten eerste wordt de afhankelijke variabele (vertegenwoordigd op de Y-as van de grafiek) herhaaldelijk gemeten in de tijd (vertegenwoordigd door de x-as) op regelmatige intervallen. Ten tweede, de studie is onderverdeeld in verschillende fasen, en de deelnemer wordt getest onder één voorwaarde per fase., De voorwaarden worden vaak aangeduid met hoofdletters: A, B, C, enzovoort. Figuur 10.2 geeft dus een ontwerp weer waarin de deelnemer eerst werd getest in één toestand (A), vervolgens in een andere toestand (B), en ten slotte opnieuw werd getest in de oorspronkelijke toestand (A). (Dit wordt een reversal design genoemd en zal binnenkort meer in detail worden besproken.)
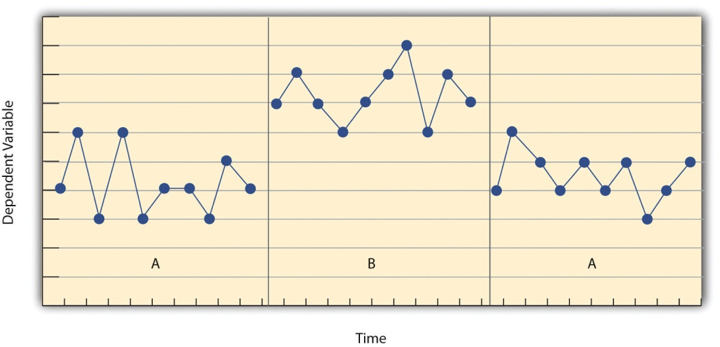
een ander belangrijk aspect van onderzoek met één onderwerp is dat de verandering van de ene toestand naar de volgende gewoonlijk niet plaatsvindt na een vaste tijd of een vast aantal waarnemingen. In plaats daarvan hangt het af van het gedrag van de deelnemer. In het bijzonder, de onderzoeker wacht tot het gedrag van de deelnemer in een toestand wordt vrij consistent van observatie naar observatie alvorens de omstandigheden te veranderen., Dit wordt soms aangeduid als de steady state strategie (Sidman, 1960). Het idee is dat wanneer de afhankelijke variabele een stabiele toestand heeft bereikt, elke verandering tussen omstandigheden relatief gemakkelijk te detecteren zal zijn. Bedenk dat we ditzelfde principe tegenkwamen bij het bespreken van experimenteel onderzoek meer in het algemeen. Het effect van een onafhankelijke variabele is gemakkelijker te detecteren wanneer de “ruis” in de gegevens wordt geminimaliseerd.
Reversal Designs
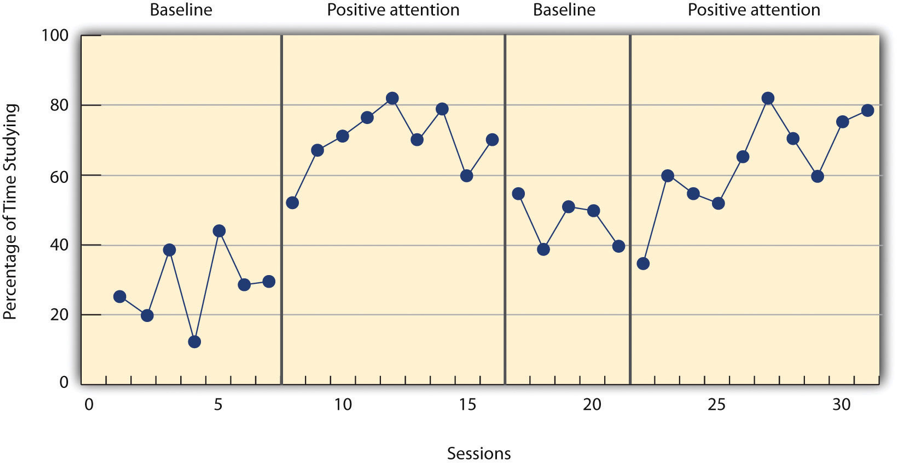
het meest fundamentele individuele onderzoeksontwerp is het reversal design, ook wel het ABA-ontwerp genoemd., Tijdens de eerste fase, A, wordt een baseline vastgesteld voor de afhankelijke variabele. Dit is het niveau van reageren voordat een behandeling wordt geïntroduceerd, en daarom is de baseline-fase een soort controlevoorwaarde. Wanneer steady state respons wordt bereikt, fase B begint als de onderzoeker introduceert de behandeling. Er kan een periode van aanpassing aan de behandeling zijn waarin het gedrag van interesse meer variabel wordt en begint te stijgen of dalen., Nogmaals, de onderzoeker wacht tot die afhankelijke variabele een steady state bereikt, zodat duidelijk is of en hoeveel het is veranderd. Ten slotte verwijdert de onderzoeker de behandeling en wacht opnieuw tot de afhankelijke variabele een stabiele toestand bereikt. Dit fundamentele omkeringsontwerp kan ook worden uitgebreid met de herintroductie van de behandeling (ABAB), een andere terugkeer naar basislijn (ABABA), enzovoort.de studie van Hall en zijn collega ‘ s was een ABAB reversal design. Figuur 10.3 benadert de gegevens voor Robbie., Het percentage van de tijd dat hij besteedde aan het bestuderen (de afhankelijke variabele) was laag tijdens de eerste baseline-fase, nam toe tijdens de eerste behandelingsfase totdat deze afvlakte, nam af tijdens de tweede baseline-fase en nam opnieuw toe tijdens de tweede behandelingsfase.
Waarom wordt de reversal—het verwijderen van de behandeling—als noodzakelijk beschouwd in dit type ontwerp? Waarom bijvoorbeeld een ABA-ontwerp gebruiken in plaats van een eenvoudiger AB-ontwerp? Merk op dat een AB-ontwerp in wezen een onderbroken tijdreeksontwerp is dat wordt toegepast op een individuele deelnemer., Bedenk dat een probleem met dat ontwerp is dat als de afhankelijke variabele verandert nadat de behandeling is ingevoerd, het niet altijd duidelijk is dat de behandeling verantwoordelijk was voor de verandering. Het is mogelijk dat iets anders rond dezelfde tijd veranderde en dat deze vreemde variabele verantwoordelijk is voor de verandering in de afhankelijke variabele., Maar als de afhankelijke variabele verandert met de introductie van de behandeling en dan terug verandert met de verwijdering van de behandeling (ervan uitgaande dat de behandeling geen permanent effect creëert), is het veel duidelijker dat de behandeling (en verwijdering van de behandeling) de oorzaak is. Met andere woorden, de omkering verhoogt de interne validiteit van de studie sterk.
Er zijn naaste verwanten van de fundamentele omkeringsopzet die de evaluatie van meer dan één behandeling mogelijk maken., In een omkering van meerdere behandelingen wordt een baseline fase gevolgd door afzonderlijke fasen waarin verschillende behandelingen worden geïntroduceerd. Een onderzoeker kan bijvoorbeeld een baseline van het bestuderen van gedrag voor een disruptieve student vast te stellen( A), vervolgens een behandeling met positieve aandacht van de leraar te introduceren (B), en vervolgens over te schakelen op een behandeling met milde straf voor het niet studeren (C). De deelnemer zou dan terug naar een baseline fase kunnen worden gebracht alvorens elke behandeling opnieuw te introduceren—misschien in omgekeerde volgorde als een manier om de effecten van overdracht te controleren., Deze bijzondere meervoudige behandeling omkering ontwerp kan ook worden aangeduid als een ABCACB ontwerp.
bij wisselende behandelingen worden twee of meer behandelingen relatief snel afgewisseld volgens een regelmatig schema. Bijvoorbeeld, positieve aandacht voor studeren kan de ene dag worden gebruikt en milde straf voor het niet studeren van de volgende, enzovoort. Of een behandeling kan ‘ s ochtends worden uitgevoerd en een andere in de middag. Het afwisselende behandelingsontwerp kan een snelle en effectieve manier zijn om behandelingen te vergelijken, maar alleen wanneer de behandelingen snel werken.,
Multiple-Baseline Designs
Er zijn twee mogelijke problemen met het omkeerontwerp—die beide te maken hebben met het verwijderen van de behandeling. Een daarvan is dat als een behandeling werkt, het onethisch kan zijn om het te verwijderen. Bijvoorbeeld, als een behandeling leek om de incidentie van zelfletsel in een ontwikkeling gehandicapt kind te verminderen, zou het onethisch zijn om die behandeling te verwijderen alleen maar om aan te tonen dat de incidentie van zelfletsel toeneemt. Het tweede probleem is dat de afhankelijke variabele niet kan terugkeren naar baseline wanneer de behandeling wordt verwijderd., Bijvoorbeeld, wanneer positieve aandacht voor studeren wordt verwijderd, kan een student blijven studeren in een verhoogd tempo. Dit zou kunnen betekenen dat de positieve aandacht een blijvend effect had op het studeren van de student, wat natuurlijk goed zou zijn. Maar het zou ook kunnen betekenen dat de positieve aandacht in de eerste plaats niet echt de oorzaak was van het toegenomen studeren. Misschien gebeurde er iets anders op ongeveer hetzelfde moment als de behandeling—bijvoorbeeld, de ouders van de student kunnen zijn begonnen hem te belonen voor goede cijfers.,
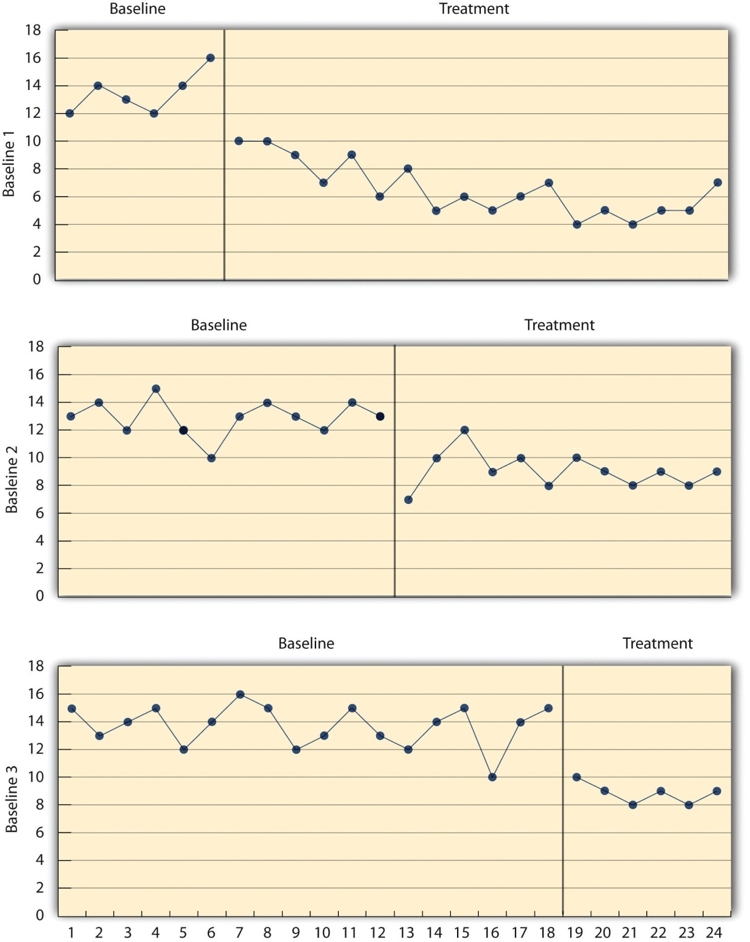
een oplossing voor deze problemen is het gebruik van een multiple-baseline-ontwerp, dat wordt weergegeven in Figuur 10.4. In één versie van het ontwerp wordt een basislijn vastgesteld voor elk van de verschillende deelnemers, en de behandeling wordt vervolgens geïntroduceerd voor elk van de deelnemers. In essentie wordt elke deelnemer getest in een AB-ontwerp. De sleutel tot dit ontwerp is dat de behandeling wordt geïntroduceerd op een ander moment voor elke deelnemer. Het idee is dat als de afhankelijke variabele verandert wanneer de behandeling voor één deelnemer wordt ingevoerd, het toeval kan zijn., Maar als de afhankelijke variabele verandert wanneer de behandeling wordt ingevoerd voor meerdere deelnemers—vooral wanneer de behandeling wordt ingevoerd op verschillende tijdstippen voor de verschillende deelnemers—dan is het uiterst onwaarschijnlijk dat een toeval.
neem als voorbeeld een studie van Scott Ross en Robert Horner (Ross & Horner, 2009). Ze waren geïnteresseerd in hoe een schoolbrede pestpreventieprogramma het pestgedrag van bepaalde probleemstudenten beïnvloedde. Op elk van de drie verschillende scholen bestudeerden de onderzoekers twee studenten die zich regelmatig hadden beziggehouden met pesten. Tijdens de baseline fase, ze observeerden de studenten gedurende 10 minuten periodes elke dag tijdens de lunch pauze en telde het aantal agressieve gedrag dat ze tentoongesteld ten opzichte van hun collega ‘ s., (De onderzoekers gebruikten handheld computers om de gegevens te registreren. Na 2 weken implementeerden ze het programma op één school. Na nog 2 weken, ze geïmplementeerd op de tweede school. En na nog 2 weken, implementeerden ze het op de derde school. Ze vonden dat het aantal agressieve gedragingen van elke student daalde kort nadat het programma werd uitgevoerd op zijn of haar school., Merk op dat als de onderzoekers slechts één school hadden gestudeerd of als ze de behandeling op alle drie de scholen op hetzelfde moment hadden ingevoerd, het onduidelijk zou zijn of de vermindering van agressief gedrag te wijten was aan het pestprogramma of iets anders dat gebeurde op ongeveer hetzelfde moment dat het werd ingevoerd (bijvoorbeeld een vakantie, een televisieprogramma, een verandering in het weer). Maar met hun multiple-baseline ontwerp, zou dit soort toeval drie keer moeten gebeuren-een zeer onwaarschijnlijke gebeurtenis-om hun resultaten te verklaren.,
in een andere versie van het multiple-baseline-ontwerp worden meerdere basislijnen vastgesteld voor dezelfde deelnemer, maar voor verschillende afhankelijke variabelen, en wordt de behandeling op een ander tijdstip voor elke afhankelijke variabele geïntroduceerd. Stel je bijvoorbeeld een studie voor naar het effect van het stellen van duidelijke doelen op de productiviteit van een kantoormedewerker die twee primaire taken heeft: het maken van sales calls en het schrijven van rapporten. Voor beide taken zouden basislijnen kunnen worden vastgesteld. De onderzoeker kan bijvoorbeeld het aantal sales calls en rapporten per week gedurende enkele weken meten., Dan zou de doelbepalende behandeling voor één van deze taken kunnen worden ingevoerd, en op een later tijdstip zou dezelfde behandeling voor de andere taak kunnen worden ingevoerd. De logica is hetzelfde als voorheen. Als de productiviteit stijgt op één taak nadat de behandeling is ingevoerd, is het onduidelijk of de behandeling de toename veroorzaakte. Maar als de productiviteit op beide taken toeneemt nadat de behandeling is ingevoerd-vooral wanneer de behandeling op twee verschillende tijdstippen wordt ingevoerd-dan lijkt het veel duidelijker dat de behandeling verantwoordelijk was.,
in nog een derde versie van het multiple-baseline-ontwerp worden meerdere basislijnen vastgesteld voor dezelfde deelnemer, maar in verschillende instellingen. Bijvoorbeeld, een basislijn kan worden vastgesteld voor de hoeveelheid tijd die een kind besteedt lezen tijdens zijn vrije tijd op school en tijdens zijn vrije tijd thuis. Dan kan een behandeling zoals positieve aandacht eerst op school en later thuis worden ingevoerd. Nogmaals, als de afhankelijke variabele verandert nadat de behandeling in elke instelling is ingevoerd, dan geeft dit de onderzoeker het vertrouwen dat de behandeling in feite verantwoordelijk is voor de verandering.,
gegevensanalyse in onderzoek met één onderwerp
naast de focus op individuele deelnemers verschilt onderzoek met één onderwerp in de manier waarop de gegevens doorgaans worden geanalyseerd. Zoals we hebben gezien in het boek, groep onderzoek omvat het combineren van gegevens over de deelnemers. Groepsgegevens worden beschreven met behulp van statistieken zoals middelen, standaardafwijkingen, Pearson ‘ s r, enzovoort om algemene patronen te detecteren. Ten slotte worden inferentiële statistieken gebruikt om te helpen beslissen of het resultaat voor de steekproef waarschijnlijk aan de bevolking zal generaliseren., Onderzoek met één onderwerp is daarentegen sterk afhankelijk van een heel andere benadering, visuele inspectie genaamd. Dit houdt in dat de gegevens van individuele deelnemers worden uitgezet zoals in dit hoofdstuk wordt getoond, die gegevens zorgvuldig worden bekeken en worden beoordeeld of en in welke mate de onafhankelijke variabele een effect heeft gehad op de afhankelijke variabele. Inferentiële statistieken worden meestal niet gebruikt.
bij het visueel inspecteren van hun gegevens houden individuele onderzoekers rekening met verschillende factoren. Een van hen is veranderingen in het niveau van de afhankelijke variabele van voorwaarde aan voorwaarde., Als de afhankelijke variabele in een toestand veel hoger of veel lager is dan in een andere, suggereert dit dat de behandeling een effect had. Een tweede factor is trend, die verwijst naar geleidelijke stijgingen of dalingen in de afhankelijke variabele over waarnemingen. Als de afhankelijke variabele begint te stijgen of te dalen met een verandering in de omstandigheden, dan suggereert dit opnieuw dat de behandeling een effect had. Het kan vooral duidelijk zijn wanneer een trend van richting verandert-bijvoorbeeld wanneer een ongewenst gedrag toeneemt tijdens de uitgangssituatie, maar dan begint af te nemen met de introductie van de behandeling., Een derde factor is latentie, de tijd die nodig is voor de afhankelijke variabele om te beginnen te veranderen na een verandering in omstandigheden. In het algemeen, als een verandering in de afhankelijke variabele begint kort na een verandering in Voorwaarden, dit suggereert dat de behandeling verantwoordelijk was.
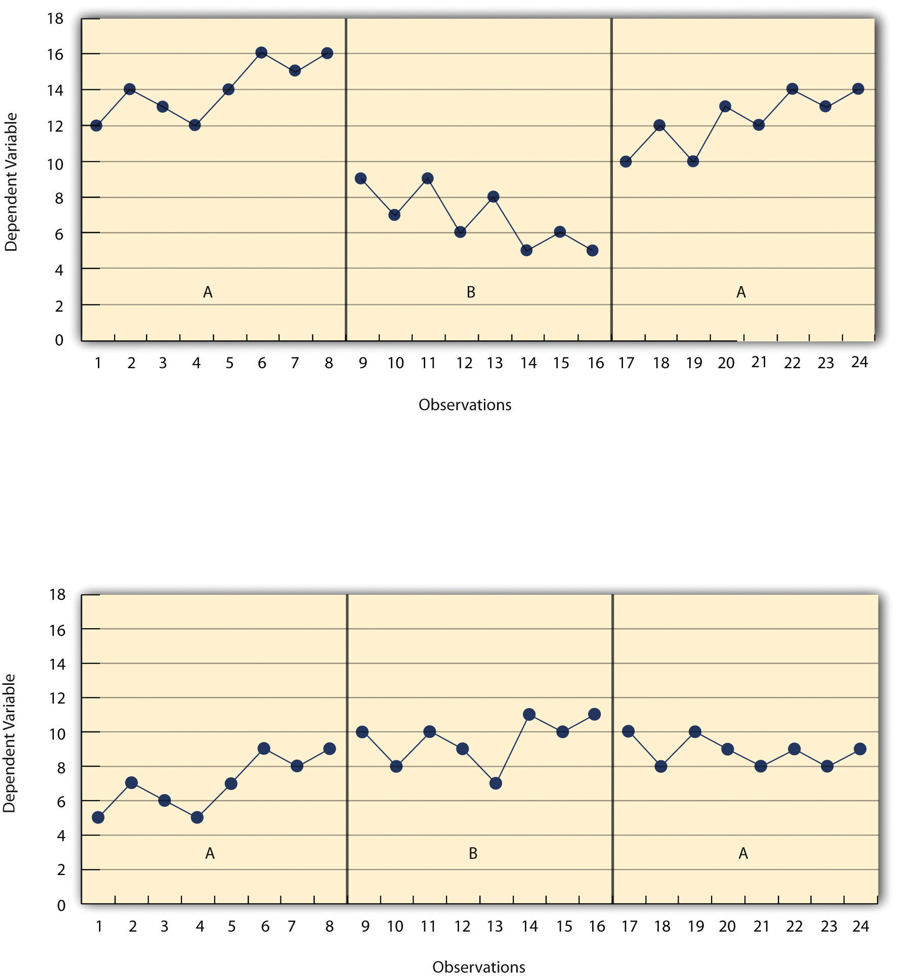
in het bovenste paneel van figuur 10.5 zijn er vrij duidelijke veranderingen in het niveau en de trend van de afhankelijke variabele van toestand tot toestand. Bovendien zijn de latenties van deze veranderingen kort; de verandering gebeurt onmiddellijk., Dit patroon van resultaten suggereert sterk dat de behandeling verantwoordelijk was voor de veranderingen in de afhankelijke variabele. In het onderste paneel van figuur 10.5 zijn de veranderingen in niveau echter vrij klein. En hoewel er een stijgende trend in de behandelingsvoorwaarde lijkt te zijn, lijkt het alsof het een voortzetting van een trend zou kunnen zijn die al tijdens baseline was begonnen. Dit patroon van resultaten suggereert sterk dat de behandeling niet verantwoordelijk was voor veranderingen in de afhankelijke variabele—tenminste niet in de mate dat single-subject onderzoekers meestal hopen te zien.,
de resultaten van individueel onderzoek kunnen ook worden geanalyseerd met behulp van statistische procedures-en dit komt steeds vaker voor. Er zijn veel verschillende benaderingen, en onderzoekers met één onderwerp blijven discussiëren welke het nuttigst zijn., Een benadering komt overeen met wat typisch wordt gedaan in groepsonderzoek. De gemiddelde en standaardafwijking van de reacties van elke deelnemer onder elke voorwaarde worden berekend en vergeleken, en inferentiële statistische tests zoals de T-test of variantieanalyse worden toegepast (Fisch, 2001). (Merk op dat het gemiddeld over de deelnemers minder gebruikelijk is.) Een andere benadering is het berekenen van het percentage non-overlapping data (PND) voor elke deelnemer (Scruggs & Mastropieri, 2001)., Dit is het percentage responsen in de behandelingsvoorwaarde dat extremer is dan de meest extreme respons in een relevante controlevoorwaarde. In de studie van Hall en zijn collega ‘s, bijvoorbeeld, waren alle metingen van Robbie’ s studietijd in de eerste behandelingsvoorwaarde groter dan de hoogste meting in de eerste baseline, voor een PND van 100%. Hoe groter het percentage niet-overlappende gegevens, hoe sterker het behandelingseffect., Toch worden formele statistische benaderingen van gegevensanalyse in onderzoek met één onderwerp over het algemeen beschouwd als een aanvulling op visuele inspectie, niet als een vervanging ervan.
- individuele onderzoeksontwerpen omvatten doorgaans het herhaaldelijk meten van de afhankelijke variabele in de loop van de tijd en het veranderen van omstandigheden (bijvoorbeeld van baseline tot behandeling) wanneer de afhankelijke variabele een steady-state heeft bereikt. Deze benadering stelt de onderzoeker in staat om te zien of veranderingen in de onafhankelijke variabele veranderingen in de afhankelijke variabele veroorzaken.,
- in een reversal-ontwerp wordt de deelnemer getest in een uitgangsconditie, vervolgens getest in een behandelingsconditie en vervolgens teruggebracht naar de uitgangswaarde. Als de afhankelijke variabele verandert met de introductie van de behandeling en dan terug verandert met de terugkeer naar baseline, levert dit sterk bewijs van een behandelingseffect.
- in een multiple-baseline ontwerp, worden basislijnen vastgesteld voor verschillende deelnemers, verschillende afhankelijke variabelen, of verschillende instellingen—en de behandeling wordt geïntroduceerd op een ander moment op elke baseline., Als de introductie van de behandeling wordt gevolgd door een verandering in de afhankelijke variabele per baseline, levert dit sterke aanwijzingen op voor een behandelingseffect.
- Single-subject onderzoekers analyseren doorgaans hun gegevens door ze grafisch te maken en oordelen over de vraag of de onafhankelijke variabele de afhankelijke variabele beïnvloedt op basis van niveau, trend en latentie.
- praktijk: ontwerp een eenvoudige single-subject studie (met behulp van een omkering of multiple-baseline ontwerp) om de volgende vragen te beantwoorden., Zorg ervoor dat u de behandeling specificeert, operationeel de afhankelijke variabele definieert, bepaalt wanneer en waar de waarnemingen zullen worden gedaan, enzovoort.
- verhoogt positieve aandacht van een ouder het tandenborstelgedrag van een kind?
- verbetert zelftesten tijdens het studeren de prestaties van een student op wekelijkse spellingstesten?
- helpt regelmatige lichaamsbeweging depressie te verlichten?
- praktijk: Maak een grafiek die de hypothetische resultaten weergeeft voor het onderzoek dat u in Oefening 1 hebt ontworpen. Schrijf een paragraaf waarin je beschrijft wat de resultaten laten zien., Zorg ervoor dat u commentaar geeft op niveau, trend en latency.
lange beschrijvingen
figuur 10.3 lange beschrijving: lijngrafiek met de resultaten van een onderzoek met een ABAB-omkering. De afhankelijke variabele was laag tijdens de eerste baseline-fase; nam toe tijdens de eerste behandeling; nam af tijdens de tweede baseline, maar was nog steeds hoger dan tijdens de eerste baseline; en was het hoogst tijdens de tweede behandelingsfase.
Figuur 10.,4 lange beschrijving: drie lijngrafieken met de resultaten van een generische multiple-baseline studie, waarin verschillende basislijnen worden vastgesteld en behandeling wordt geïntroduceerd aan de deelnemers op verschillende tijdstippen.
voor Baseline 1 wordt de behandeling gestart met een kwart van de weg naar het onderzoek. De afhankelijke variabele varieert tussen 12 en 16 eenheden tijdens de baseline, maar daalt af tot 10 eenheden tijdens de behandeling en neemt meestal af tot het einde van de studie, variërend tussen 4 en 10 eenheden.
voor Baseline 2 wordt de behandeling halverwege het onderzoek gestart., De afhankelijke variabele varieert tussen 10 en 15 eenheden tijdens de baseline en heeft dan een sterke daling tot 7 eenheden wanneer de behandeling wordt gestart. De afhankelijke variabele neemt echter snel na de daling toe tot 12 eenheden en varieert tussen 8 en 10 eenheden tot het einde van de studie.
voor Baseline 3 wordt driekwart van de way in het onderzoek geïntroduceerd. De afhankelijke variabele varieert tussen 12 en 16 eenheden voor het grootste deel tijdens de basislijn, met een daling naar beneden tot 10 eenheden., Wanneer de behandeling wordt gestart, daalt de afhankelijke variabele tot 10 eenheden en varieert vervolgens tussen 8 en 9 eenheden tot het einde van de studie.
figuur 10.5 lange Beschrijving: Twee grafieken met de resultaten van een generiek onderzoek met één proefpersoon met een ABA-ontwerp. In de eerste grafiek, onder voorwaarde A, is het niveau hoog en de trend neemt toe. Onder voorwaarde B is het niveau veel lager dan onder voorwaarde A en neemt de trend af. Onder voorwaarde A weer, niveau is ongeveer zo hoog als de eerste keer en de trend neemt toe., Voor elke verandering is de latentie kort, wat suggereert dat de behandeling de reden is voor de verandering.
in de tweede grafiek, onder voorwaarde A, is het niveau relatief laag en neemt de trend toe. Onder conditie B is het niveau iets hoger dan tijdens conditie A en neemt de trend iets toe. Onder conditie A is het niveau weer iets lager dan bij conditie B en neemt de trend iets af. Het is moeilijk om de latentie van deze veranderingen te bepalen, omdat elke verandering nogal klein is, wat suggereert dat de behandeling niet effectief is.,
De onderzoeker wacht tot het gedrag van de deelnemer in één toestand redelijk consistent wordt van observatie tot observatie alvorens de omstandigheden te veranderen. Op deze manier zal elke verandering tussen omstandigheden gemakkelijk te detecteren zijn.
een onderzoeksmethode waarbij de onderzoeker gegevens verzamelt over een uitgangssituatie, de behandeling introduceert en de observatie voortzet totdat een steady state is bereikt, en ten slotte de behandeling verwijdert en de deelnemer observeert totdat hij terugkeert naar een steady state.,
het niveau van respons voordat een behandeling wordt ingevoerd en werkt daarom als een soort controlevoorwaarde.
een baseline fase wordt gevolgd door afzonderlijke fasen waarin verschillende behandelingen worden geïntroduceerd.
twee of meer behandelingen worden relatief snel afgewisseld volgens een regelmatig schema.
een baseline wordt vastgesteld voor meerdere deelnemers en de behandeling wordt vervolgens op een ander tijdstip aan elke deelnemer gegeven.,
het plotten van de gegevens van individuele deelnemers, het onderzoeken van de gegevens en het beoordelen van de vraag of en in welke mate de onafhankelijke variabele een effect had op de afhankelijke variabele.
of de gegevens hoger of lager zijn op basis van een visuele inspectie van de gegevens; een verandering in het niveau impliceert dat de ingevoerde behandeling een effect heeft gehad.
de geleidelijke toename of afname van de afhankelijke variabele bij waarnemingen.
De tijd die nodig is voordat de afhankelijke variabele begint te veranderen na een verandering in omstandigheden.,
het percentage responsen in de behandelingsvoorwaarde dat extremer is dan de meest extreme respons in een relevante controlevoorwaarde.