Ondersteuning Vector Machine of SVM is een van de meest populaire begeleide leeralgoritmen, die wordt gebruikt voor classificatie en regressie problemen. Echter, in de eerste plaats, het wordt gebruikt voor Classificatieproblemen in Machine Learning.
Het doel van het SVM-algoritme is om de beste lijn-of beslissingsgrens te creëren die N-dimensionale ruimte in klassen kan scheiden, zodat we het nieuwe gegevenspunt in de toekomst gemakkelijk in de juiste categorie kunnen plaatsen., Deze beste beslissingsgrens wordt een hypervlak genoemd.
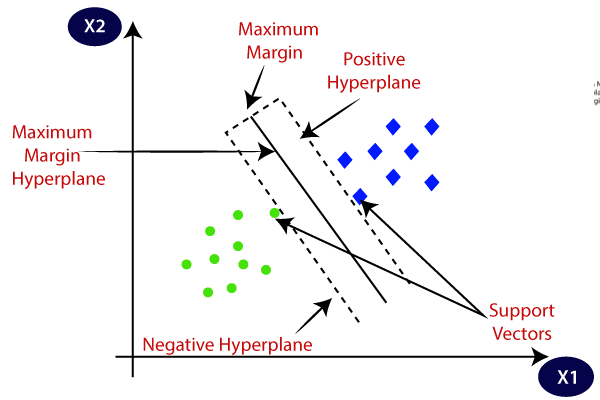
SVM kiest de extreme punten / vectoren die helpen bij het maken van het hypervlak. Deze extreme gevallen worden genoemd als steunvectoren, en vandaar wordt het algoritme genoemd als Steunvectormachine. Neem het onderstaande diagram waarin er twee verschillende categorieën zijn die worden geclassificeerd met behulp van een beslissingsgrens of hypervlak:
voorbeeld: SVM kan worden begrepen met het voorbeeld dat we hebben gebruikt in de KNN classifier., Stel dat we een vreemde kat zien die ook een aantal eigenschappen van honden heeft, dus als we een model willen dat nauwkeurig kan identificeren of het een kat of hond is, dan kan zo ‘ n model gemaakt worden met behulp van het SVM algoritme. We zullen eerst Ons model trainen met veel foto ‘ s van katten en honden, zodat het kan leren over de verschillende kenmerken van katten en honden, en dan testen we het met dit vreemde wezen. Dus als support vector creëert een beslissingsgrens tussen deze twee gegevens (kat en hond) en kies extreme gevallen (support vectoren), het zal het extreme geval van Kat en hond te zien., Op basis van de steunvectoren, zal het classificeren als een kat. Overweeg het onderstaande diagram:
SVM-algoritme kan worden gebruikt voor gezichtsdetectie, beeldclassificatie, tekstcategorisatie, enz.
typen SVM
SVM kunnen uit twee typen bestaan:
- lineair SVM: lineair SVM wordt gebruikt voor lineair scheidbare gegevens, wat betekent dat als een dataset in twee klassen kan worden ingedeeld met behulp van een enkele rechte lijn, dergelijke gegevens lineair scheidbare gegevens worden genoemd, en classifier wordt gebruikt genaamd lineair SVM classifier.,
- niet-lineaire SVM: niet-lineaire SVM wordt gebruikt voor niet-lineair gescheiden gegevens, wat betekent dat als een dataset niet kan worden geclassificeerd met behulp van een rechte lijn, dergelijke gegevens worden genoemd als niet-lineaire gegevens en gebruikte classifier wordt genoemd als niet-lineaire SVM classifier.
hypervlak en ondersteunt vectoren in het SVM-algoritme:
hypervlak: er kunnen meerdere regels/beslissingsgrenzen zijn om de klassen in de N-dimensionale ruimte te scheiden, maar we moeten de beste beslissingsgrens vinden die helpt om de gegevenspunten te classificeren. Deze beste grens staat bekend als het hypervlak van SVM.,
De afmetingen van het hypervlak zijn afhankelijk van de eigenschappen die aanwezig zijn in de dataset, wat betekent dat als er 2 eigenschappen zijn (zoals weergegeven in afbeelding), hypervlak een rechte lijn zal zijn. En als er 3 kenmerken zijn, dan is hypervlak een 2-dimensionaal vlak.
We maken altijd een hypervlak met een maximale marge, wat de maximale afstand tussen de gegevenspunten betekent.
Ondersteuningsvectoren:
de gegevenspunten of vectoren die het dichtst bij het hypervlak liggen en die de positie van het hypervlak beïnvloeden, worden Ondersteuningsvector genoemd., Aangezien deze vectoren het hypervlak ondersteunen, vandaar een Steunvector genoemd.
Hoe werkt SVM?
Lineaire SVM:
de werking van het SVM-algoritme kan worden begrepen met behulp van een voorbeeld. Stel dat we een dataset hebben met twee tags (groen en blauw), en de dataset heeft twee functies x1 en x2. We willen een classifier die het paar(x1, x2) van coördinaten in groen of blauw kan classificeren. Overweeg de onderstaande afbeelding:
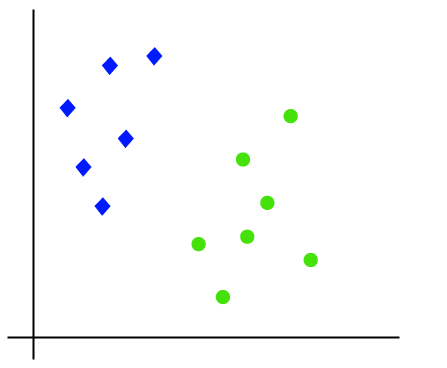
omdat het 2-d spatie is, kunnen we deze twee klassen eenvoudig scheiden door gewoon een rechte lijn te gebruiken., Maar er kunnen meerdere regels zijn die deze klassen kunnen scheiden. Neem de onderstaande afbeelding:
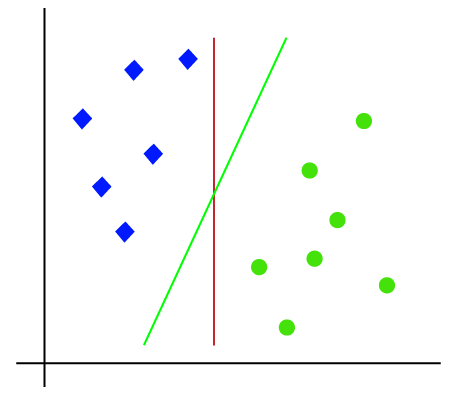
vandaar dat het SVM-algoritme helpt om de beste lijn-of beslissingsgrens te vinden; deze beste grens of regio wordt genoemd als een hypervlak. SVM algoritme vindt het dichtstbijzijnde punt van de lijnen van beide klassen. Deze punten worden steunvectoren genoemd. De afstand tussen de vectoren en het hypervlak wordt als marge genoemd. En het doel van SVM is om deze marge te maximaliseren. Het hypervlak met maximale marge wordt het optimale hypervlak genoemd.,
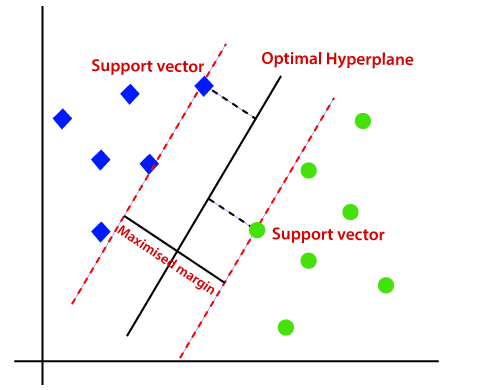
niet-lineaire SVM:
Als gegevens lineair geordend zijn, dan kunnen we ze scheiden met behulp van een rechte lijn, maar voor niet-lineaire gegevens kunnen we geen enkele rechte tekenen. Overweeg de onderstaande afbeelding:
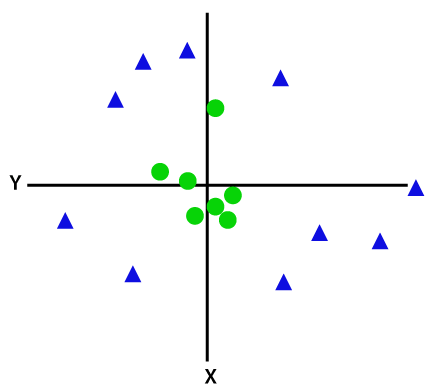
dus om deze gegevenspunten te scheiden, moeten we nog een dimensie toevoegen. Voor lineaire gegevens hebben we twee dimensies x en y gebruikt, dus voor niet-lineaire gegevens voegen we een derde dimensie z toe., Het kan worden berekend als:
z=x2 +y2
door de derde dimensie toe te voegen, wordt de monsterruimte zoals hieronder afbeelding:
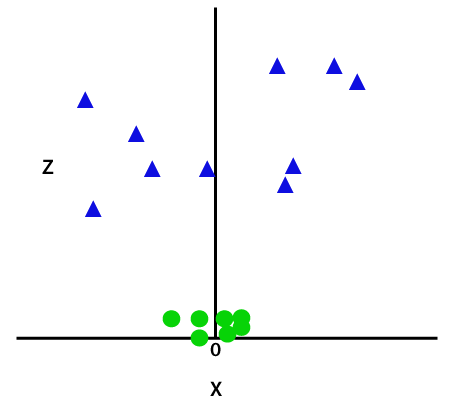
dus nu zal SVM de datasets op de volgende manier in klassen verdelen. Neem de onderstaande afbeelding:
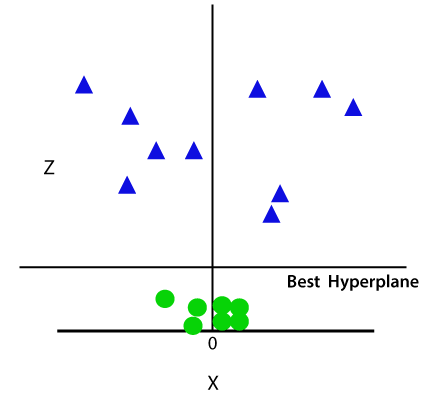
aangezien we in 3-d ruimte zijn, lijkt het dus op een vlak evenwijdig aan de x-as. Als we het converteren in 2d ruimte met z = 1, dan wordt het als:
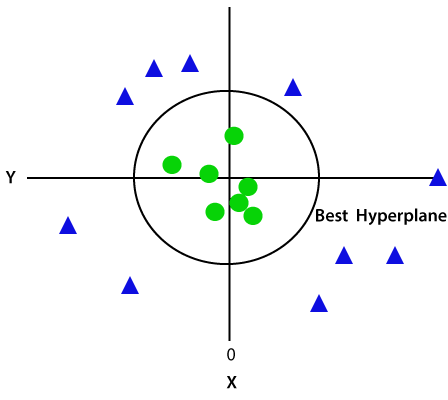
vandaar krijgen we een omtrek van straal 1 in het geval van niet-lineaire gegevens.,
Python implementatie van Support Vector Machine
nu zullen we het SVM algoritme implementeren met behulp van Python. Hier zullen we dezelfde dataset user_data gebruiken, die we hebben gebruikt in logistieke regressie en KNN classificatie.
- stap voor gegevensverwerking
tot de stap voor gegevensverwerking blijft de code hetzelfde. Hieronder staat de code:
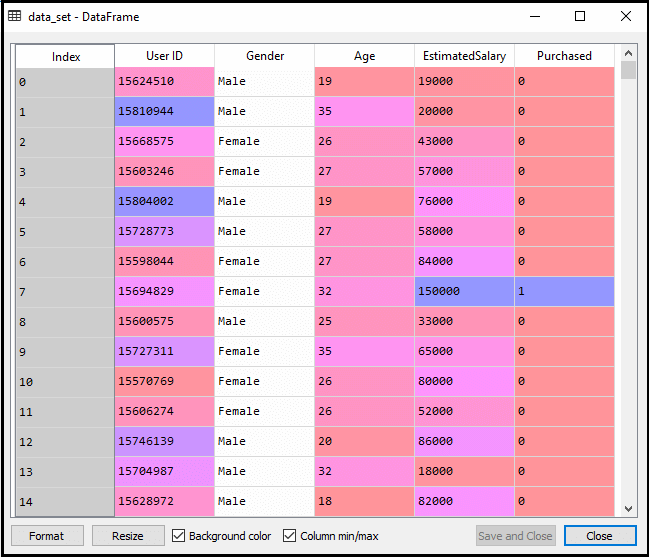
na het uitvoeren van de bovenstaande code, zullen we de gegevens vooraf verwerken., De code geeft de dataset als:
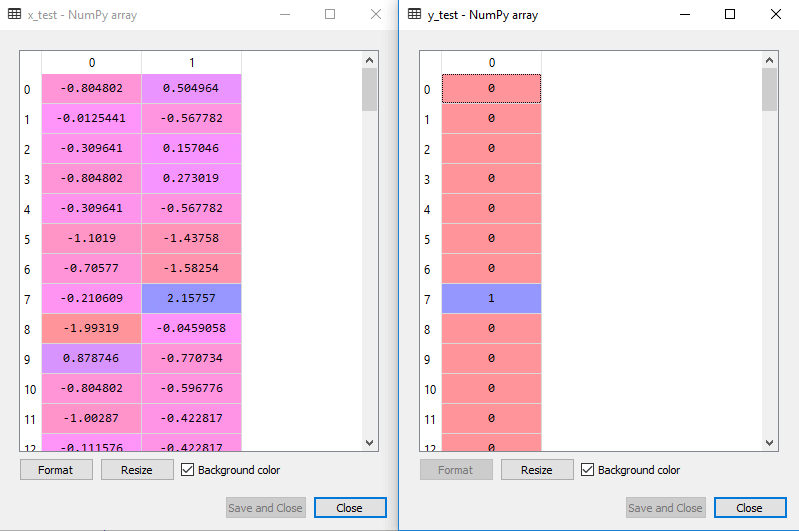
de geschaalde uitvoer voor de testset zal zijn:
de SVM-classifier aanpassen aan de trainingsset:
nu zal de trainingsset worden gemonteerd op de SVM-classifier. Om de SVM classifier te maken, zullen we SVC class importeren vanuit Sklearn.svm bibliotheek. Hieronder staat de code:
in de bovenstaande code hebben we kernel=’linear’ gebruikt, omdat we hier SVM maken voor lineair scheidbare data. We kunnen het echter veranderen voor niet-lineaire gegevens., En dan hebben we de classifier op de trainingsdataset(x_train, y_train)
uitvoer:
De modelprestaties kunnen worden gewijzigd door de waarde van C(Regularisatiefactor), gamma en kernel te veranderen.
- voorspellen van het resultaat van de testset:
nu zullen we de uitvoer van de testset voorspellen. Hiervoor maken we een nieuwe vector y_pred. Hieronder staat de code:
na het verkrijgen van de y_pred vector, kunnen we het resultaat van y_pred en y_test vergelijken om het verschil tussen de werkelijke waarde en de voorspelde waarde te controleren.,
uitvoer: Hieronder is de uitvoer voor de voorspelling van de testset:

- het creëren van de verwarmingsmatrix:
nu zullen we de prestaties van de SVM classifier zien dat hoeveel onjuiste voorspellingen er zijn in vergelijking met de Logistic regression classifier. Om de confusion matrix te creëren, moeten we de confusion_matrix functie van de sklearn bibliotheek importeren. Na het importeren van de functie, zullen we het noemen met behulp van een nieuwe variabele cm. De functie neemt twee parameters, voornamelijk y_true (de werkelijke waarden) en y_pred (de beoogde waarde return door de classifier)., Hieronder is de code ervoor:
Output:
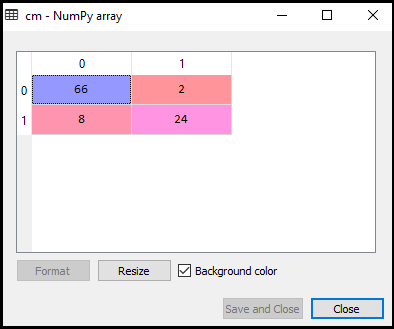
zoals we kunnen zien in de bovenstaande uitvoerafbeelding, zijn er 66+24= 90 correcte voorspellingen en 8+2= 10 correcte voorspellingen. Daarom kunnen we zeggen dat ons SVM-model verbeterd is ten opzichte van het logistieke regressiemodel.,
- visualiseren van het resultaat van de trainingsset:
nu zullen we het resultaat van de trainingsset visualiseren, hieronder is de code ervoor:
uitvoer:
door het uitvoeren van de bovenstaande code krijgen we de uitvoer als:
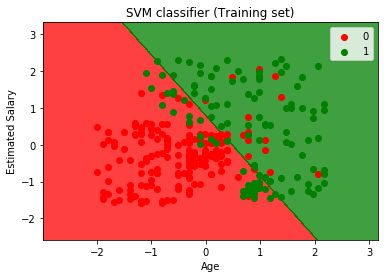
zoals we kunnen zien, lijkt de bovenstaande uitvoer op de logistische regressie output. In de uitvoer kregen we de rechte lijn als hypervlak omdat we een lineaire kernel in de classifier hebben gebruikt. En we hebben hierboven ook besproken dat Voor de 2d-ruimte, het hypervlak in SVM een rechte lijn is.,
- het resultaat van de testset visualiseren:
uitvoer:
door de bovenstaande code uit te voeren, krijgen we de uitvoer als:
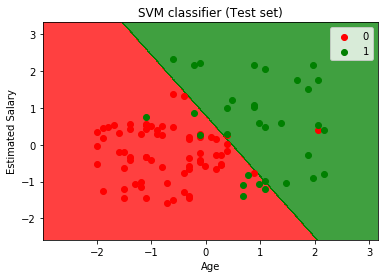
zoals we kunnen zien in de bovenstaande uitvoerafbeelding, heeft de SVM-classifier de gebruikers verdeeld in twee regio ‘ s (gekocht of niet gekocht). Gebruikers die de SUV gekocht zijn in de rode regio met de rode scatter points. En gebruikers die de SUV niet hebben gekocht zijn in de groene regio met groene scatter points. Het hyperplan heeft de twee klassen verdeeld in gekochte en niet gekochte variabele.