aanname van de normaliteit van de afhankelijke variabele
De onafhankelijke t-test vereist dat de afhankelijke variabele ongeveer normaal over elke groep wordt verdeeld.
opmerking: technisch gezien zijn het de reststoffen die normaal verdeeld moeten worden, maar voor een onafhankelijke t-test geven beide hetzelfde resultaat.,
u kunt dit testen met behulp van een aantal verschillende tests, maar de Shapiro-Wilks test van normaliteit of een grafische methode, zoals een Q-Q Plot, zijn zeer gebruikelijk. U kunt deze tests uitvoeren met behulp van SPSS-statistieken, waarvan de procedure te vinden is in onze Testing for Normality gids. De t-test wordt echter beschreven als een robuuste test met betrekking tot de aanname van normaliteit. Dit betekent dat enige afwijking van de normaliteit geen grote invloed heeft op type I foutenpercentages. De uitzondering hierop is als de verhouding van de kleinste tot de grootste groep groter is dan 1.,5 (grootste in vergelijking met kleinste).
Wat te doen als u niet aan de veronderstelling van normaliteit
Als u vindt dat één of beide van uw groep gegevens is niet ongeveer normaal verdeeld en maten groepen verschillen sterk, hebt u twee mogelijkheden: (1) het omzetten van uw gegevens, zodat de gegevens normaal verdeeld is (om dit te doen in SPSS Statistics zie onze gids over op het Transformeren van Gegevens), of (2) het uitvoeren van de Mann-Whitney U test, dat is een niet-parametrische test die niet vereist dat de aanname van normaliteit (voor het uitvoeren van deze test in SPSS Statistics zie onze gids over op de Mann-Whitney U Test).,
aanname van homogeniteit van variantie
De onafhankelijke t-test gaat ervan uit dat de varianties van de twee groepen die u meet in de populatie gelijk zijn. Als uw varianties ongelijk zijn, kan dit het type I foutenpercentage beïnvloeden. De aanname van homogeniteit van variantie kan worden getest met behulp van Levene ‘ s Test of Equality of Variances, die wordt geproduceerd in SPSS-statistieken bij het uitvoeren van de onafhankelijke t-testprocedure., Als u Levene ‘ s Test van gelijkheid van varianties in SPSS-statistieken hebt uitgevoerd, zult u een resultaat krijgen dat vergelijkbaar is met dat hieronder:

Deze test voor homogeniteit van variantie levert een F-statistiek en een significantie waarde (p-waarde). We houden ons voornamelijk bezig met de significantiewaarde – als deze groter is dan 0,05 (d.w.z., p > .05), kunnen onze groepsvarianties als gelijk worden behandeld. Echter, als p < 0,05, hebben we ongelijke varianties en we hebben de aanname van homogeniteit van varianties geschonden.,
het overwinnen van een schending van de aanname van homogeniteit van variantie
als de test van Levene voor de gelijkheid van varianties statistisch significant is, wat aangeeft dat de groepsvarianties ongelijk zijn in de populatie, kunt u deze schending corrigeren door niet de samengevoegde schatting voor de foutterm voor de t-statistiek te gebruiken, maar in plaats daarvan een aanpassing van de vrijheidsgraden te gebruiken met behulp van de Welch-Satterthwaite methode., In alle werkelijkheid, zult u waarschijnlijk nooit gehoord van deze aanpassingen, omdat SPSS statistieken verbergt deze informatie en gewoon labels de twee opties als “equal variances assumed” En “Equal variances not assumed” zonder expliciet vermelding van de onderliggende tests gebruikt., U kunt echter het bewijs van deze tests zien als volgt:
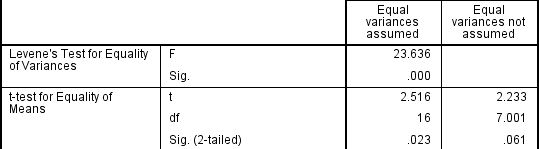
uit het resultaat van de Test van Levene voor de gelijkheid van varianties kunnen we de nulhypothese dat er geen verschil is in de varianties tussen de groepen verwerpen en de alternatieve hypothese accepteren dat er een statistisch significant verschil is in de varianties tussen groepen., Het effect van het niet kunnen aannemen van gelijke varianties is duidelijk in de laatste kolom van het bovenstaande cijfer waar we een vermindering van de waarde van de T-statistiek en een grote vermindering van de vrijheidsgraden (df) zien. Dit heeft als gevolg dat de p-waarde boven het kritische significantieniveau van 0,05 stijgt. In dit geval aanvaarden we daarom de alternatieve hypothese niet en accepteren we dat er geen statistisch significante verschillen tussen de middelen zijn. Dit zou niet onze conclusie zijn geweest als we niet hadden getest op homogeniteit van varianties.