Inleiding
lineaire regressie, ook bekend als eenvoudige lineaire regressie of bivariate lineaire regressie, wordt gebruikt wanneer we de waarde van een afhankelijke variabele willen voorspellen op basis van de waarde van een onafhankelijke variabele. U kunt bijvoorbeeld lineaire regressie gebruiken om te begrijpen of de examenprestaties kunnen worden voorspeld op basis van revisietijd (d.w.z.,, uw afhankelijke variabele zou zijn “exam performance”, gemeten van 0-100 mark, en uw onafhankelijke variabele zou zijn “revision time”, gemeten in uren). Afwisselend, kunt u lineaire regressie gebruiken om te begrijpen of sigarettenverbruik kan worden voorspeld op basis van de duur van het roken (dat wil zeggen, uw afhankelijke variabele zou zijn “sigarettenverbruik”, gemeten in termen van het aantal sigaretten dagelijks verbruikt, en uw onafhankelijke variabele zou zijn “roken duur”, gemeten in dagen). Als u twee of meer onafhankelijke variabelen hebt, in plaats van slechts één, moet u meerdere regressie gebruiken., Als alternatief, als je gewoon wilt vaststellen of er een lineaire relatie bestaat, kun je Pearson ‘ s correlatie gebruiken.
opmerking: de afhankelijke variabele wordt ook de outcome, target of criterion variabele genoemd, terwijl de onafhankelijke variabele ook de predictor, verklarende of regressor variabele wordt genoemd. Uiteindelijk, welke term je ook gebruikt, is het het beste om consistent te zijn. We zullen deze als afhankelijke en onafhankelijke variabelen in deze gids.,
in deze gids laten we u zien hoe u lineaire regressie kunt uitvoeren met behulp van Stata, en hoe u de resultaten van deze test kunt interpreteren en rapporteren. Echter, voordat we u kennis laten maken met deze procedure, moet u de verschillende veronderstellingen begrijpen waaraan uw gegevens moeten voldoen om lineaire regressie om u een geldig resultaat te geven. We bespreken deze veronderstellingen vervolgens.
Stata
aannames
Er zijn zeven “aannames” die ten grondslag liggen aan lineaire regressie. Als aan een van deze zeven veronderstellingen niet wordt voldaan, kunt u uw gegevens niet analyseren met behulp van lineair, omdat u geen geldig resultaat krijgt., Aangezien aannames # 1 en # 2 betrekking hebben op uw keuze van variabelen, kunnen ze niet worden getest voor het gebruik van Stata. Echter, moet u beslissen of uw studie voldoet aan deze aannames voordat u verder gaat.
- aanname # 1: uw afhankelijke variabele moet worden gemeten op het continue niveau., Voorbeelden van dergelijke continue variabelen zijn hoogte (gemeten in voet en inches), temperatuur (gemeten in oC), salaris (gemeten in US dollars), revisietijd (gemeten in uren), intelligentie (gemeten met behulp van IQ-score), reactietijd (gemeten in milliseconden), testprestaties (gemeten van 0 tot 100), omzet (gemeten in aantal transacties per maand), enzovoort. Als u niet zeker weet of uw afhankelijke variabele continu is (dat wil zeggen, gemeten op het interval of ratio niveau), zie onze types of Variable guide.,
- aanname # 2: uw onafhankelijke variabele moet worden gemeten op continu of categorisch niveau. Als u echter een categorisch onafhankelijke variabele hebt, is het meer gebruikelijk om een onafhankelijke t-test (voor 2 groepen) of eenrichtingsanova (voor 3 groepen of meer) te gebruiken. In het geval u niet zeker bent, voorbeelden van categorische variabelen zijn geslacht (bijv., 2 groepen: man en vrouw), etniciteit (bijv., 3 groepen: Kaukasisch, Afro-Amerikaans en Hispanic), fysieke activiteit niveau (bijv., 4 groepen: sedentair, laag, matig en hoog), en beroep (bijv.,, 5 groepen: chirurg, Arts, Verpleegkundige, tandarts, therapeut). In deze gids laten we u de lineaire regressieprocedure en Stata-uitvoer zien wanneer zowel uw afhankelijke als onafhankelijke variabelen op een continu niveau werden gemeten.
gelukkig kunt u aannames controleren #3, #4, #5, #6 en # 7 met Stata. Bij het overgaan tot veronderstellingen #3, #4, #5, #6 en # 7, We stellen voor om ze in deze volgorde te testen, omdat het een volgorde vertegenwoordigt waarin, als een schending van de aanname niet kan worden gecorrigeerd, je niet langer lineaire regressie kunt gebruiken., In feite, wees niet verbaasd als uw gegevens een of meer van deze veronderstellingen faalt, omdat dit vrij typisch is bij het werken met real-world data in plaats van leerboek voorbeelden, die vaak alleen laten zien hoe je lineaire regressie uit te voeren wanneer alles goed gaat. Maak je echter geen zorgen, want zelfs als je gegevens niet voldoen aan bepaalde veronderstellingen, is er vaak een oplossing om dit te overwinnen (bijvoorbeeld, het transformeren van uw gegevens of het gebruik van een andere statistische test in plaats daarvan)., Vergeet niet dat als je niet controleert of je gegevens aan deze aannames voldoen of je ze onjuist test, de resultaten die je krijgt bij het uitvoeren van lineaire regressie mogelijk niet geldig zijn.
- aanname #3: Er moet een lineair verband zijn tussen de afhankelijke en onafhankelijke variabelen. Hoewel er een aantal manieren zijn om te controleren of er een lineaire relatie bestaat tussen je twee variabelen, raden we aan om een scatterplot te maken met behulp van Stata, waar je de afhankelijke variabele kunt plotten tegen je onafhankelijke variabele., U kunt dan visueel inspecteren de scatterplot om te controleren op lineariteit. Uw scatterplot kan er ongeveer als volgt uitzien:
als de relatie in uw scatterplot niet lineair is, moet u ofwel een niet-lineaire regressieanalyse Uitvoeren of uw gegevens” transformeren”, wat u kunt doen met Stata.
- aanname # 4: Er mogen geen significante uitschieters zijn. Uitschieters zijn gewoon enkele gegevenspunten binnen uw gegevens die niet het gebruikelijke patroon volgen (bijv.,, in een studie van 100 studenten ‘ IQ scores, waar de gemiddelde score was 108 met slechts een kleine variatie tussen de studenten, een student had een score van 156, dat is zeer ongebruikelijk,en kan haar zelfs in de top 1% van IQ scores wereldwijd). De volgende scatterplots benadrukken het potentiële effect van uitschieters:
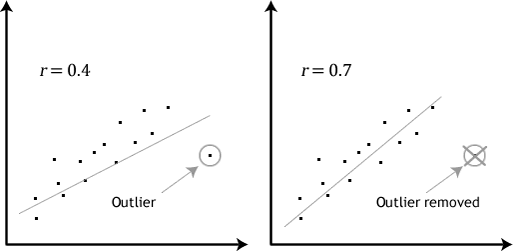
het probleem met uitschieters is dat ze een negatief effect kunnen hebben op de regressievergelijking die wordt gebruikt om de waarde van de afhankelijke variabele te voorspellen op basis van de onafhankelijke variabele., Dit verandert de output die Stata produceert en vermindert de voorspellende nauwkeurigheid van uw resultaten. Gelukkig kunt u Stata gebruiken om casewise diagnostics uit te voeren om u te helpen mogelijke uitschieters te detecteren.
- aanname # 5: U moet onafhankelijk zijn van waarnemingen, die u eenvoudig kunt controleren met behulp van de Durbin-Watson-statistiek, een eenvoudige test die u kunt uitvoeren met behulp van Stata.
- aanname # 6: Uw gegevens moeten homoscedasticiteit tonen, waarbij de varianties langs de lijn van best fit gelijk blijven als u langs de lijn beweegt., De twee scatterplots hieronder geven eenvoudige voorbeelden van gegevens die aan deze aanname voldoen en een die de aanname niet voldoet:
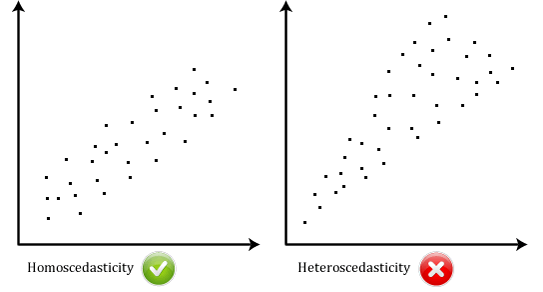
wanneer u uw eigen gegevens analyseert, hebt u geluk als uw scatterplot eruit ziet als een van de twee hierboven. Terwijl deze helpen om de verschillen in gegevens die voldoet aan of in strijd is met de veronderstelling van homoscedasticiteit te illustreren, real-world data is vaak een stuk rommeliger., U kunt controleren of uw gegevens homoscedasticiteit toonden door het plotten van de regressie gestandaardiseerde reststoffen tegen de regressie gestandaardiseerde voorspelde waarde.
- aanname # 7: ten slotte moet u controleren of de reststoffen (fouten) van de regressielijn ongeveer normaal verdeeld zijn. Twee gemeenschappelijke methoden om deze aanname te controleren omvatten het gebruik van een histogram (met een gesuperponeerde normale curve) of een normale P-P grafiek.
in de praktijk, controle op aannames #3, #4, #5, #6 en # 7 zal waarschijnlijk het grootste deel van uw tijd in beslag nemen bij het uitvoeren van lineaire regressie., Het is echter geen moeilijke taak, en Stata biedt alle tools die u nodig hebt om dit te doen.
in het hoofdstuk Procedure illustreren we de Stata-procedure die nodig is om lineaire regressie uit te voeren, ervan uitgaande dat er geen aannames zijn geschonden. Ten eerste geven we het voorbeeld dat we gebruiken om de lineaire regressieprocedure in Stata te verklaren.
Stata
voorbeeld
Studies tonen aan dat bewegen kan helpen hartziekte te voorkomen. Binnen redelijke grenzen, hoe meer je traint, hoe minder risico je hebt op het lijden aan hart-en vaatziekten., Een manier waarop lichaamsbeweging uw risico op hart-en vaatziekten vermindert, is door het verminderen van een vet in uw bloed, genaamd cholesterol. Hoe meer je traint, hoe lager je cholesterolconcentratie. Bovendien is onlangs aangetoond dat de hoeveelheid tijd die u besteedt aan het kijken naar TV – een indicator van een sedentaire levensstijl – een goede voorspeller van hart-en vaatziekten kan zijn (dat wil zeggen, dat hoe meer TV Je kijkt, hoe groter uw risico op hart-en vaatziekten).,
daarom besloot een onderzoeker om te bepalen of de cholesterolconcentratie gerelateerd was aan de tijd die werd besteed aan TV kijken bij normaal gezonde mannen van 45 tot 65 jaar (een risicocategorie van mensen). Bijvoorbeeld, als mensen meer tijd besteden aan TV kijken, is hun cholesterolconcentratie ook gestegen (een positieve relatie); of is het tegenovergestelde gebeurd? De onderzoeker wilde ook het aandeel van de cholesterolconcentratie weten dat de tijd besteed aan TV-kijken zou kunnen verklaren, evenals de mogelijkheid om de cholesterolconcentratie te voorspellen., De onderzoeker kon dan bepalen of bijvoorbeeld mensen die acht uur per dag TV keken gevaarlijk hoge cholesterolconcentraties hadden in vergelijking met mensen die slechts twee uur TV keken.
voor de uitvoering van de analyse nam de onderzoeker 100 gezonde mannelijke deelnemers in de leeftijd van 45 tot 65 jaar aan. De hoeveelheid tijd besteed aan het kijken naar TV (dat wil zeggen, de onafhankelijke variabele, time_tv) en cholesterol concentratie (dat wil zeggen, de afhankelijke variabele, cholesterol) werden geregistreerd voor alle 100 deelnemers., Uitgedrukt in variabele termen, de onderzoeker wilde cholesterol regresseren op time_tv.
opmerking: het voorbeeld en de gegevens die voor deze gids worden gebruikt zijn fictief. We hebben ze zojuist gemaakt voor de doeleinden van deze gids.
Stata
instellingen in Stata
Opmerking: Het maakt niet uit of u eerst de afhankelijke of onafhankelijke variabele maakt.
na het maken van deze twee variabelen – time_tv en cholesterol-hebben we de scores voor elk in de twee kolommen van de Data Editor (bewerken) spreadsheet (d.w.z., de tijd in uren dat de deelnemers TV keken in de linkerkolom (d.w.z. time_tv, de onafhankelijke variabele), en de cholesterolconcentratie van de deelnemers in mmol/L in de rechterkolom (d.w.z. cholesterol, de afhankelijke variabele), zoals hieronder weergegeven:
gepubliceerd met schriftelijke toestemming van StataCorp LP.,
Stata
testprocedure in Stata
In deze sectie laten we u zien hoe u uw gegevens kunt analyseren met behulp van lineaire regressie in Stata wanneer de zes aannames in de vorige sectie, aannames, niet zijn geschonden. U kunt lineaire regressie uitvoeren met behulp van code of Stata ‘ s grafische gebruikersinterface (GUI). Nadat u uw analyse hebt uitgevoerd, laten we u zien hoe u uw resultaten kunt interpreteren. Kies eerst of u code of Stata ‘ s grafische gebruikersinterface (GUI) wilt gebruiken.,
Code
de code voor het uitvoeren van lineaire regressie op uw gegevens neemt de vorm aan:
regress DependentVariable IndependentVariable
deze code wordt ingevoerd in het kader hieronder:
gepubliceerd met schriftelijke toestemming van statacorp lp.,
gebruikmakend van ons voorbeeld waar de afhankelijke variabele cholesterol is en de onafhankelijke variabele time_tv, zou de vereiste code zijn:
regress cholesterol time_tv
Opmerking 1: U moet precies zijn wanneer u de code invoert in het doos. De code is “hoofdlettergevoelig”. Bijvoorbeeld, als u “Cholesterol” waar de “C” is hoofdletters in plaats van kleine letters (d.w.z.,, een kleine “c”), wat het zou moeten zijn, krijgt u een foutmelding als het volgende:
Opmerking 2: Als u nog steeds de foutmelding krijgt in Opmerking 2: hierboven, is het de moeite waard om de naam te controleren die u uw twee variabelen in de Data Editor hebt gegeven wanneer u uw bestand instelt (zie het Data Editor scherm hierboven)., In de box aan de rechterkant van het Data Editor scherm, is het de manier waarop u uw variabelen spelde in de
sectie, niet de
sectie die u in de code moet invoeren (zie hieronder voor onze afhankelijke variabele). Dit lijkt misschien voor de hand liggend, maar het is een fout die soms wordt gemaakt, resulterend in de fout in Noot 2 hierboven.
voer daarom de code in, regresseer cholesterol time_tv en druk op de” Return/Enter ” knop op uw toetsenbord.,
gepubliceerd met schriftelijke toestemming van StataCorp LP.
u kunt hier de Stata-uitvoer zien die zal worden geproduceerd.,
Grafische User Interface (GUI)
De drie stappen die nodig zijn uit te voeren lineaire regressie in staten bestaan 12 en 13 worden hieronder getoond:
- Klik op Statistieken > Lineaire modellen en verwante > Lineaire regressie op de main menu, zoals hieronder weergegeven:
Gepubliceerd met schriftelijke toestemming van de StataCorp LP.,
u krijgt het dialoogvenster Regress-Linear regressie te zien:
gepubliceerd met schriftelijke toestemming van StataCorp LP.
- selecteer cholesterol vanuit het keuzevakje afhankelijke variabele: en time_tv vanuit het keuzevakje onafhankelijke variabelen:. U krijgt het volgende scherm:
gepubliceerd met schriftelijke toestemming van StataCorp LP.,
-
klik op de knop
. Dit zal de output genereren.
Stata
Output van lineaire regressieanalyse in Stata
als uw gegevens aanname #3 (d.w.z. Er was een lineair verband tussen uw twee variabelen), #4 (d.w.z. er waren geen significante uitschieters), aanname # 5 (d.w.z. u had onafhankelijkheid van waarnemingen), aanname # 6 (d.w.z. uw gegevens vertoonden homoscedasticiteit) en aanname #7 (d.w.z.,, de residuals (errors) waren ongeveer normaal verdeeld), die we eerder in de aannames sectie hebben uitgelegd, hoeft u alleen de volgende lineaire regressie output in Stata te interpreteren:
gepubliceerd met schriftelijke toestemming van StataCorp LP.,
De output bestaat uit vier belangrijke informatiestukken: (A) De R2-waarde (rij”R-kwadraat”) vertegenwoordigt de variantieverhouding in de afhankelijke variabele die kan worden verklaard door onze onafhankelijke variabele (technisch is het de variantieverhouding die wordt verklaard door het regressiemodel boven en boven het gemiddelde model). Echter, R2 is gebaseerd op de steekproef en is een positief bevooroordeelde schatting van het aandeel van de variantie van de afhankelijke variabele verantwoord door het regressiemodel (d.w.z.,, het is te groot); (b) een aangepaste R2-waarde (“adj R-kwadraat” rij), die positieve bias corrigeert om een waarde te leveren die verwacht zou worden in de populatie; (c) de F-waarde, vrijheidsgraden (“F( 1, 98)”) en statistische significantie van het regressiemodel (“Prob > F” rij); en (d) de coëfficiënten voor de constante en onafhankelijke variabele (“Coef.”kolom), dat is de informatie die je nodig hebt om de afhankelijke variabele, cholesterol, te voorspellen met behulp van de onafhankelijke variabele, time_tv.
in dit voorbeeld, R2 = 0.151. Aangepast R2 = 0,143 (tot 3 d.p.,), wat betekent dat de onafhankelijke variabele, time_tv, 14,3% van de variabiliteit van de afhankelijke variabele, cholesterol, in de populatie verklaart. Gecorrigeerde R2 is ook een schatting van de effectgrootte, die op 0,143 (14,3%) wijst op een gemiddelde effectgrootte, volgens Cohen ‘ s (1988) classificatie. Normaal gesproken is R2 echter niet de aangepaste R2 die in de resultaten wordt gerapporteerd. In dit voorbeeld is het regressiemodel statistisch significant, F (1, 98) = 17,47, p=.0001., Dit geeft aan dat, over het algemeen, het toegepaste model statistisch significant de afhankelijke variabele, cholesterol kan voorspellen.
opmerking: We presenteren de output van de lineaire regressieanalyse hierboven. Aangezien u uw gegevens echter had moeten testen op de veronderstellingen die we eerder in het gedeelte veronderstellingen hebben uitgelegd, moet u ook de Stata-uitvoer interpreteren die werd geproduceerd toen u op deze veronderstellingen testte. Dit omvat: (a) de scatterplots die u gebruikt om te controleren of er een lineaire relatie tussen uw twee variabelen (d.w.z.,, Aanname #3); (b) casewise diagnostics te controleren waren er geen significante uitschieters (i.e., Aanname #4); (c) de output van de Durbin-Watson-statistiek om te controleren voor de onafhankelijkheid van waarnemingen (i.e., Aanname #5); (d) een scatterplot van de regressie gestandaardiseerde residuen tegen de gestandaardiseerde regressie voorspelde waarde om te bepalen of uw gegevens bleek homoscedasticity (i.e., Aanname #6); en een histogram (met er bovenop de normale curve) en de Normal P-P Plot om te controleren of de residuen (fouten) waren ongeveer normaal verdeeld is (ofwel, Aanname #7)., Vergeet ook niet dat als uw gegevens niet voldoen aan een van deze veronderstellingen, de output die u krijgt van de lineaire regressieprocedure (dat wil zeggen, de output die we hierboven bespreken) niet langer relevant zal zijn, en u kan een andere statistische test uit te voeren om uw gegevens te analyseren.,
Stata
rapportage van de output van de lineaire regressieanalyse
wanneer u de output van uw lineaire regressie rapporteert, is het goed om: (A) Een inleiding op de door u uitgevoerde analyse op te nemen; (b) informatie over uw steekproef, inclusief ontbrekende waarden; (c) de waargenomen F-waarde, vrijheidsgraden en significantieniveau (d.w.z. de p-waarde); (d) het percentage van de variabiliteit in de afhankelijke variabele dat wordt verklaard door de onafhankelijke variabele (d.w.z. uw aangepaste R2).); en (e) de regressievergelijking voor uw model., Op basis van de resultaten hierboven konden we de resultaten van deze studie als volgt rapporteren:
- Algemeen
een lineaire regressie stelde vast dat de dagelijkse tijd die we aan het TV-kijken besteden statistisch significant de cholesterolconcentratie kon voorspellen, F(1, 98) = 17,47, p = .0001 en tijd besteed aan het kijken naar TV verantwoordelijk voor 14,3% van de verklaarde variabiliteit in cholesterolconcentratie. De regressievergelijking was: voorspelde cholesterolconcentratie = -2.135 + 0,044 x (tijd besteed aan tv kijken).,
naast het rapporteren van de resultaten zoals hierboven, kan een diagram worden gebruikt om uw resultaten visueel te presenteren. Bijvoorbeeld, je zou dit kunnen doen met behulp van een scatterplot met vertrouwen en voorspelling intervallen (hoewel het niet erg gebruikelijk is om de laatste toe te voegen). Dit kan het makkelijker maken voor anderen om uw resultaten te begrijpen. Bovendien kunt u uw lineaire regressievergelijking gebruiken om voorspellingen te doen over de waarde van de afhankelijke variabele op basis van verschillende waarden van de onafhankelijke variabele., Hoewel Stata deze waarden niet produceert als onderdeel van de lineaire regressieprocedure hierboven, is er een procedure in Stata die u kunt gebruiken om dit te doen.