we zien licht als altijd in rechte lijnen, maar als lichtgolven in de buurt van een barrière passeren, neigen ze om die barrière heen te buigen en zich uit te spreiden. Diffractie van licht treedt op wanneer een lichtgolf langs een hoek of door een opening of spleet gaat die fysiek ongeveer de grootte heeft van, of zelfs kleiner is dan de golflengte van dat licht.,

een zeer eenvoudige demonstratie van diffractie kan worden uitgevoerd door uw hand voor een lichtbron te houden en langzaam twee vingers te sluiten terwijl het licht tussen hen wordt waargenomen. Als de vingers elkaar benaderen en heel dicht bij elkaar komen, begin je een reeks donkere lijnen parallel aan de vingers te zien. De parallelle lijnen zijn eigenlijk diffractiepatronen. Dit fenomeen kan ook optreden wanneer licht wordt “gebogen” rond deeltjes die op dezelfde orde van grootte als de golflengte van het licht., Een goed voorbeeld hiervan is de diffractie van zonlicht door wolken die we vaak een zilveren randje noemen, geïllustreerd in Figuur 1 met een prachtige zonsondergang boven de oceaan.
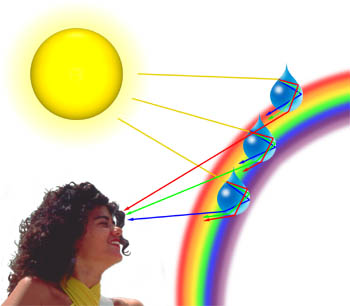
We kunnen vaak pasteltinten van blauw, roze, paars en groen waarnemen in wolken die worden gegenereerd wanneer licht wordt verspreid door waterdruppels in de wolken. De hoeveelheid diffractie hangt af van de golflengte van licht, met kortere golflengten die onder een grotere hoek dan langere (in feite, blauw en violet licht worden verspreid onder een hogere hoek dan rood licht)., Als een lichtgolf die door de atmosfeer reist een druppel water tegenkomt, zoals hieronder wordt geïllustreerd, wordt deze eerst gebroken bij het water:lucht-interface, dan wordt het gereflecteerd als het opnieuw de interface tegenkomt. De straal, die nog steeds in de waterdruppel reist, wordt opnieuw gebroken als hij de interface voor de derde keer raakt. Deze laatste interactie met de interface breekt het licht terug in de atmosfeer, maar het diffracteert ook een deel van het licht zoals hieronder afgebeeld., Dit diffractie-element leidt tot een fenomeen dat bekend staat als Cellini ‘ s halo (ook bekend als het Heiligenschein-effect) waar een heldere ring van licht de schaduw van het hoofd van de waarnemer omringt.
De termen diffractie en verstrooiing worden vaak door elkaar gebruikt en worden als bijna synoniem beschouwd. Diffractie beschrijft een gespecialiseerd geval van lichtverstrooiing waarbij een object met regelmatig herhalende kenmerken (zoals een diffractierooster) een ordelijke diffractie van licht in een diffractiepatroon produceert., In de echte wereld zijn de meeste objecten zeer complex van vorm en moeten worden beschouwd als samengesteld uit vele individuele diffractiekenmerken die collectief een willekeurige verstrooiing van licht kunnen produceren.
een van de klassieke en meest fundamentele concepten met betrekking tot diffractie is het optische diffractie-experiment met één gleuf, dat Voor het eerst werd uitgevoerd in het begin van de negentiende eeuw. Wanneer een lichtgolf zich voortplant door een spleet (of opening) hangt het resultaat af van de fysieke grootte van de opening ten opzichte van de golflengte van de invallende bundel., Dit wordt geïllustreerd in Figuur 3, uitgaande van een coherente, monochromatische golf, uitgezonden door de puntbron S, vergelijkbaar met het licht dat geproduceerd zouden worden door een laser, gaat door het diafragma d en is diffracted, met het primaire incident lichtbundel landing op het punt P en de eerste secundaire maxima die op het punt Q.
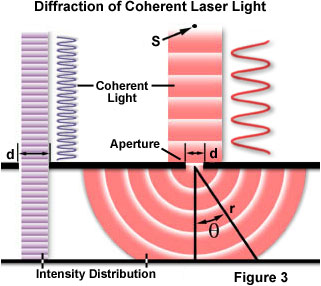
Zoals getoond in de linker kant van de figuur, als de golflengte (λ) is veel kleiner dan het diafragma breedte (d), de golf gewoon reist verder in een rechte lijn, zoals het zou als het ware een deeltje of geen diafragma aanwezig waren., Wanneer de golflengte echter de grootte van de diafragma overschrijdt, ervaren we diffractie van het licht volgens de vergelijking:
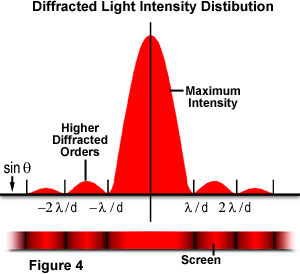
waarbij θ de hoek is tussen de invallende centrale voortplantingsrichting en het eerste minimum van het diffractiepatroon. Het experiment produceert een helder centraal maximum dat aan beide zijden wordt geflankeerd door secundaire maxima, waarbij de intensiteit van elk volgend secundair maximum afneemt naarmate de afstand tot het centrum toeneemt. Figuur 4 illustreert dit punt met een grafiek van stralingsintensiteit versus diffractiestraal., Merk op dat de minima die zich tussen secundaire maxima bevinden zich in veelvouden van π.
Dit experiment werd voor het eerst verklaard door Augustin Fresnel die, samen met Thomas Young, belangrijke bewijzen leverde die bevestigen dat licht in golven reist. Uit de bovenstaande figuren zien we hoe een coherent, monochromatisch licht (in dit voorbeeld, laserverlichting) dat van punt L wordt uitgezonden, wordt gediffecteerd door diafragma d., Fresnel ging ervan uit dat de amplitude van de eerste orde maxima op punt Q (gedefinieerd als eQ) zou worden gegeven door de vergelijking:
waar A de amplitude van de invallende Golf is, r de afstand tussen d en Q is, en f(χ) een functie is van χ, een inclinatiefactor die door Fresnel wordt geïntroduceerd.
diffractie van licht
onderzoek hoe een lichtbundel diffracteert wanneer deze door een smalle spleet of opening gaat. Pas de golflengte en de diafragmagrootte aan en observeer hoe dit het patroon van de diffractieintensiteit beïnvloedt.,
diffractie van licht speelt een cruciale rol bij het beperken van het oplossend vermogen van elk optisch instrument (bijvoorbeeld: camera ‘ s, verrekijkers, telescopen, microscopen en het oog). Het oplossend vermogen is het vermogen van het optische instrument om afzonderlijke beelden van twee aangrenzende punten te produceren. Dit wordt vaak bepaald door de kwaliteit van de lenzen en spiegels in het instrument en de eigenschappen van het omringende medium (meestal lucht). De golfachtige aard van licht dwingt een ultieme grens aan het oplossend vermogen van alle optische instrumenten.,
onze discussies over diffractie hebben een spleet gebruikt als de opening waardoor licht wordt diffracteerd. Alle optische instrumenten hebben echter cirkelvormige openingen, bijvoorbeeld de pupil van een oog of het cirkelvormige membraan en lenzen van een microscoop. Cirkelvormige openingen produceren diffractiepatronen vergelijkbaar met die hierboven beschreven, behalve dat het patroon van nature een cirkelvormige symmetrie vertoont. De wiskundige analyse van de diffractiepatronen die door een cirkelvormige opening worden geproduceerd, wordt beschreven met de vergelijking:
waarbij θ (1) de hoekpositie is van de eerste orde diffractieminima (de eerste donkere ring), λ de golflengte van het invallende licht, d de diameter van de opening en 1.22 een constante is. Onder de meeste omstandigheden is de hoek θ(1) zeer klein, zodat de benadering dat de sin en tan van de hoek bijna gelijke opbrengsten zijn:
uit deze vergelijkingen blijkt dat het centrale maximum recht evenredig is met λ/d waardoor dit maximum meer gespreid is voor langere golflengten en voor kleinere openingen., De secundaire mimina van diffractie stelde een grens aan de nuttige vergroting van objectieve lenzen in optische microscopie, toe te schrijven aan inherente diffractie van licht door deze lenzen. Hoe perfect de lens ook is, het beeld van een door de lens geproduceerde puntbron gaat gepaard met secundaire en hogere orde maxima. Dit kon alleen worden geëlimineerd als de lens een oneindige diameter had. Twee objecten gescheiden door een afstand kleiner dan θ (1) kan niet worden opgelost, ongeacht hoe hoog het vermogen van vergroting., Terwijl deze vergelijkingen werden afgeleid voor het beeld van een puntbron van licht een oneindige afstand van de opening, is het een redelijke benadering van het oplossend vermogen van een microscoop wanneer d wordt vervangen door de diameter van de objectieve lens.
als twee objecten zich op een afstand D van elkaar bevinden en zich op een afstand L van een waarnemer bevinden, is de hoek (uitgedrukt in radialen) tussen hen:
waardoor we in staat zijn om de laatste twee vergelijkingen te condenseren tot:
waarbij D (0) de minimale afstand tussen de objecten is die het mogelijk maakt ze op te lossen. Met behulp van deze vergelijking, kan het menselijk oog objecten oplossen gescheiden door een afstand van 0,056 millimeter, maar de fotoreceptoren in het netvlies zijn niet heel dicht genoeg bij elkaar om deze mate van resolutie toe te staan, en 0,1 millimeter is een realistischer aantal onder normale omstandigheden.
het oplossend vermogen van optische microscopen wordt bepaald door een aantal factoren, waaronder de besproken factoren, maar in de meest ideale omstandigheden is dit aantal ongeveer 0,2 micrometer., Dit aantal moet rekening houden met optische uitlijning van de microscoop, kwaliteit van de lenzen, evenals de overheersende golflengten van licht gebruikt om het beeld van het monster. Hoewel het vaak niet nodig is om de exacte oplossende kracht van elke doelstelling te berekenen (en in de meeste gevallen een verspilling van tijd zou zijn), is het belangrijk om de mogelijkheden van de microscooplenzen te begrijpen als ze van toepassing zijn op de echte wereld.
bijdragende auteurs
Mortimer Abramowitz – Olympus America, Inc. Twee Corporate Center Drive. Melville, New York, 11747.
Michael W., Davidson-National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., DE Florida State University, Tallahassee, Florida, 32310.