Dit is de eerste in een drie postseries. Het tweede artikel gaat over het berekenen van Big-O. Het derde artikel gaat over het begrijpen van de formele definitie van Big-O.
Big-O notatie was vroeger een heel eng concept voor mij. Ik dacht dat dit is hoe “echte” programmeurs praatten over hun code. Het was allemaal meer eng omdat de academische beschrijvingen (zoals Wikipedia) maakte me weinig zin. Dit is frustrerend omdat de onderliggende concepten zijn eigenlijk niet zo moeilijk.,
simpel gezegd, Big-O notatie is hoe programmeurs praten overalgorithmen. Algoritmen zijn een ander eng onderwerp dat Ik zal behandelen in een ander bericht, maar voor onze doeleinden, laten we zeggen dat “algoritme” betekent een functie in uw programma (dat is niet te ver weg). De Big-Onotatie van een functie wordt bepaald door hoe deze reageert op verschillende ingangen. Hoe langzamer is het als we het een lijst geven van 1000 dingen om aan te werken in plaats van een lijst van 1 ding?
overweeg deze code:
def item_in_list(to_check, the_list): for item in the_list: if to_check == item: return True return False
dus als we deze functie als item_in_list(2, ) noemen, zou het vrij snel moeten zijn., We lus over elk ding in de lijst en als we het eerste argument voor onze functie vinden, retourneer True. Als we aan het einde komen en we het niet vinden, geef dan vals terug.
de “complexiteit” van deze functie is O(n). Ik zal zo uitleggen wat dit betekent, maar laten we deze wiskundesyntax opsplitsen. O(n) wordt gelezen” Order of N”omdat de O functie ook bekend staat als de Order functie. Ik denk dat dit komt omdat we een approximatie doen, die handelt in “ordes van grootte”.,
“orden van grootte” is een andere wiskundige term die het verschil tussen klassen van getallen vertelt. Denk aan het verschil tussen 10 en 100. Als je je 10 van je dichtste vrienden en 100 mensen voorstelt, is dat een heel groot verschil. Op dezelfde manier is het verschil tussen 1.000 en 10.000 vrij groot (in feite is het het verschil tussen een junker auto en een licht gebruikte). Het blijkt dat in benadering, zolang je binnen een orde van grootte bent,je vrij dichtbij bent., Als je het aantal kauwgomballen in een machine zou raden, zou je binnen een orde van grootte zijn als je 200 ballen zou zeggen. 10.000 kauwgomballen zou ver weg zijn.

figuur 1: een kauwgomballenmachine waarvan het aantal kauwgomballen waarschijnlijk in de Orde van grootte van 200 ligt.
terug naar ontleden O(n), dit zegt dat als we een grafiek zouden maken van de tijd die nodig is om deze functie uit te voeren met verschillende ingangen (bijvoorbeeld een array van 1 item, 2 items, 3 items, enz.), We zouden zien dat het ongeveer overeenkomt met het aantal items in de array., Dit wordt een lineaire grafiek genoemd. Dit betekent dat de lijn in principe recht is als je hem zou grafieken.
sommigen van u hebben misschien begrepen dat als in het bovenstaande codevoorbeeld ons item altijd het eerste item in de lijst was, onze code echt snel zou zijn! Dit is waar, maar Big-O is alles over de geschatte slechtste-caseprestaties van iets doen. Het slechtste geval voor de bovenstaande code isdat het ding dat we zoeken niet in de lijst staat. (Opmerking: de wiskundige term hiervoor is “bovengrens”, wat betekent dat het gaat over de mathematische limiet van awfulness).,
Als u een grafiek voor deze functies wilt zien, negeert u de functie O()en wijzigt u de variabele n voor x. Je kunt dat dan intypen in Wolfram Alpha als “plot x” die je een diagonaal zal laten zien. De reden dat je n omruilt voor x is dat hun grafische programma x als variabelnaam gebruikt omdat het overeenkomt met de xaxis. De x-as wordt groter van links naar rechts komt overeen met het geven van grotere en grotere arrays aan uw functie., De y-as vertegenwoordigt de tijd, dus hoe hoger de lijn, hoe langzamer deze is.
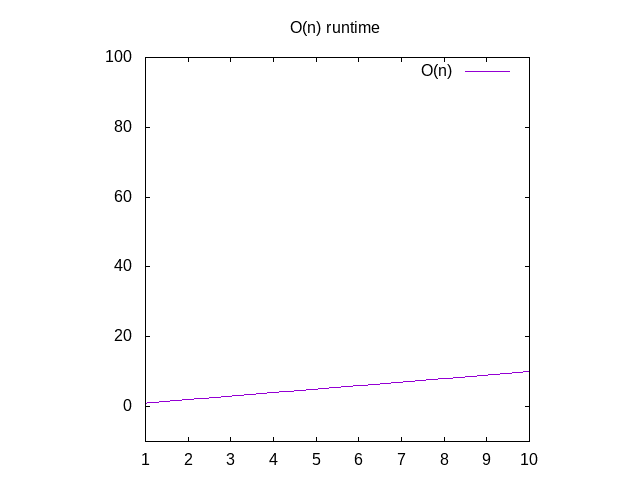
Figuur 2: Runtime karakteristieken van een o(n) functie
dus wat zijn enkele andere voorbeelden hiervan?
overweeg deze functie:
def is_none(item): return item is None
Dit is een beetje een dom voorbeeld, maar heb even geduld. Deze functie heet O(1) wat “constante tijd”wordt genoemd. Wat dit betekent is hoe groot onze input is, het duurt altijd even veel tijd om dingen te berekenen., Als je teruggaat naar Wolfram en plot 1, zul je zien dat het altijd hetzelfde blijft, ongeacht hoe ver we rechts gaan. Als je in een lijst van 1 miljoen gehele getallen passeert, duurt het ongeveer dezelfde tijd als als je in een lijst van 1 geheel getal passeert. Constante tijd wordt beschouwd als het beste scenario voor een functie.
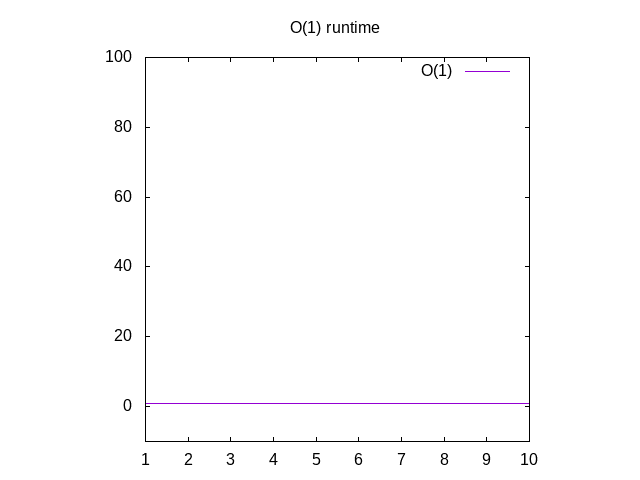
Figuur 3: Runtime kenmerken van een O(1) functie
beschouw deze functie:
Hieronder is een vergelijking van elk van deze grafieken, ter referentie., U kunt zien dat een O(n^2) functie zeer snel langzaam zal worden, terwijl iets dat in constante tijd werkt veel beter zal zijn. Dit is vooral handig als het gaat om datastructuren, die Ik zal posten over binnenkort.
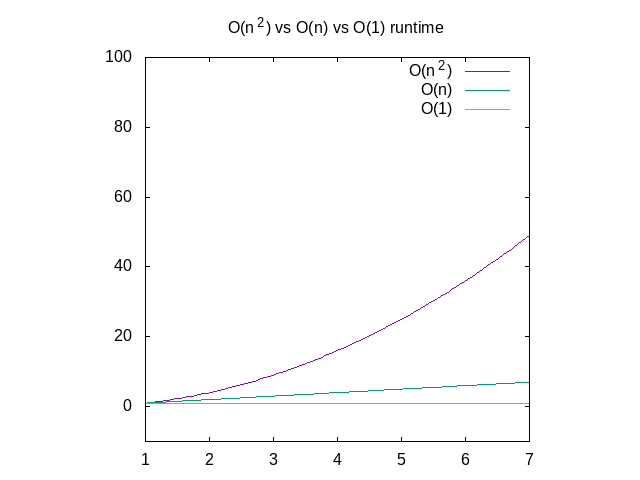
Figuur 4: vergelijking van o(n2) vs o(n) vs o(1) functies
Dit is een vrij hoog niveau overzicht van Big-O notatie, maar hopelijk maakt u kennis met het onderwerp., Er is een coursera cursus die je een dieper inzicht in dit onderwerp kan geven, maar wees gewaarschuwd dat het snel in wiskundige notatie zal springen. Als hier iets niet klopt, stuur me dan een e-mail.
Update: ik heb ook geschreven over het berekenen van Big-O.
Ik denk erover om een boek over dit onderwerp te schrijven. Als dit iets is wat je wilt zien, geef dan hier je interesse in.