weerstanden vs. inductoren
inductoren gedragen zich niet op dezelfde manier als weerstanden. Terwijl weerstanden zich eenvoudig tegen de stroomstroom door hen verzetten( door een spanning recht evenredig met de stroom te laten vallen), verzetten inductoren zich tegen veranderingen in stroom door hen, door een spanning recht evenredig met de snelheid van verandering van stroom te laten vallen.
in overeenstemming met de wet van Lenz is deze geïnduceerde spanning altijd van een zodanige polariteit dat wordt geprobeerd de stroom op zijn huidige waarde te houden., Dat wil zeggen, als de stroom toeneemt in omvang, zal de geïnduceerde spanning “duwen tegen” de stroomstroom; als de stroom afneemt, zal de polariteit omkeren en “duwen met” de stroom tegen de daling.
deze oppositie tegen de huidige verandering wordt reactantie genoemd, in plaats van weerstand., Wiskundig uitgedrukt is de relatie tussen de over de inductor dalende spanning en de snelheid van de stroomverandering door de inductor als volgt:

wisselstroom in een eenvoudig inductief Circuit
de uitdrukking di/dt is een van de calculus, wat betekent dat de snelheid van verandering van momentane stroom (i) in de tijd, in ampère per seconde.
de inductantie (L) is in Henrys, en de momentane spanning (e) is natuurlijk in volt., Soms vindt u de snelheid van de momentane spanning uitgedrukt als “v” in plaats van “e” (v = L di/dt), maar het betekent precies hetzelfde.
om te laten zien wat er gebeurt met wisselstroom, laten we een eenvoudig inductorcircuit analyseren:
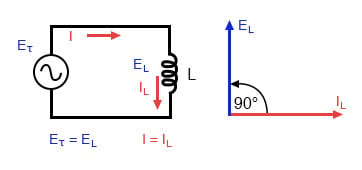
Pure inductieve circuit: inductorstroom verlaagt inductorspanning met 90°.
als we de stroom en spanning voor dit zeer eenvoudige circuit zouden plotten, zou het er ongeveer zo uitzien:

zuiver inductief circuit, golfvormen.,
onthoud dat de spanning die over een inductor is gedaald, een reactie is tegen de verandering in de stroom die erin zit.
daarom is de momentane spanning nul wanneer de momentane stroom op een piek is (nulverandering, of niveauhelling, op de huidige sinusgolf), en de momentane spanning is op een piek waar de momentane stroom op maximale verandering is (de punten van de steilste helling op de huidige golf, waar deze de nullijn overschrijdt).
Dit resulteert in een spanningsgolf die 90° uit fase is met de huidige golf., Kijkend naar de grafiek, lijkt de spanningsgolf een “voorsprong” op de huidige golf te hebben; de spanning “leidt” de stroom en de stroom “blijft” achter de spanning.

stroom vertraagt spanning met 90° in een zuiver inductief circuit.
Het wordt nog interessanter als we het vermogen voor dit circuit plotten:

in een zuiver inductief circuit kan het momentane vermogen positief of negatief zijn.,
omdat het momentane vermogen het product is van de momentane spanning en de momentane stroom (p=ie), is het vermogen gelijk aan nul wanneer de momentane stroom of spanning nul is. Wanneer de momentane stroom en spanning beide positief zijn (boven de lijn), is het vermogen positief.
net als bij het weerstandvoorbeeld is het vermogen ook positief wanneer de momentane stroom en spanning beide negatief zijn (onder de lijn).,
echter, omdat de stroom-en spanningsgolven 90° uit fase zijn, zijn er momenten waarop de ene positief is en de andere negatief, wat resulteert in even vaak voorkomende negatieve momentane vermogens.
Wat is negatief vermogen?
maar wat betekent negatief vermogen? Het betekent dat de inductor energie terug naar het circuit vrijmaakt, terwijl een positief vermogen betekent dat het vermogen van het circuit absorbeert.,
aangezien de positieve en negatieve vermogenscycli in de loop van de tijd gelijk zijn in grootte en DUUR, Geeft de inductor net zoveel vermogen terug naar het circuit af als het absorbeert over het hele traject van een volledige cyclus.
in de praktijk betekent dit dat de reactantie van een inductor netto-energie van nul afvoert, in tegenstelling tot de weerstand van een weerstand, die energie in de vorm van warmte afvoert. Let wel, Dit is alleen voor perfecte inductoren, die geen draadweerstand hebben.
reactantie vs., Weerstand
de oppositie van een inductor tegen stroomverandering vertaalt zich in een oppositie tegen wisselstroom in het algemeen, die per definitie altijd verandert in momentane magnitude en richting.
Deze weerstand tegen wisselstroom is vergelijkbaar met weerstand, maar verschilt in die zin dat het altijd resulteert in een faseverschuiving tussen stroom en spanning, en het verdrijft nulvermogen. Vanwege de verschillen heeft het een andere naam: reactantie. Reactantie op AC wordt uitgedrukt in ohm, net als weerstand, behalve dat het wiskundige symbool X is in plaats van R.,
om specifiek te zijn, wordt de reactantie geassocieerd met een inductor gewoonlijk gesymboliseerd door de hoofdletter X met een letter L als subscript, als volgt: XL.
aangezien inductoren de spanning laten dalen in verhouding tot de snelheid van stroomverandering, zullen ze meer spanning laten dalen voor sneller veranderende stromen, en minder spanning voor langzamer veranderende stromen. Dit betekent dat de reactantie in ohm voor elke inductor recht evenredig is met de frequentie van de wisselstroom., De exacte formule voor het bepalen van de reactantie is als volgt:

als we een 10 mH-inductor blootstellen aan frequenties van 60, 120 en 2500 Hz, zal deze de reactanties in onderstaande tabel manifesteren.
Reactantie van een 10 mH inductor:
| Frequentie (Hertz) | Reactantie (Ohm) |
| 60 | 3.7699 |
| 120 | 7.5398 |
| 2500 | 157.,0796 |
In de reactantievergelijking heeft de term” 2nf ” (alles aan de rechterkant behalve de L) een speciale betekenis op zich. Het is het aantal radialen per seconde dat de wisselstroom “roteert” bij, als je je een cyclus van AC voorstelt om de rotatie van een volledige cirkel weer te geven.
een radiaal is een eenheid van hoekmeting: er zijn 2π radialen in een volledige cirkel, net zoals er 360° zijn in een volledige cirkel., Als de alternator die AC produceren een dubbelpolige eenheid is, zal het één cyclus voor elke volledige omwenteling van schachtrotatie produceren, die elke 2π radialen, of 360°is.
als deze constante van 2π wordt vermenigvuldigd met de frequentie in Hertz (cycli per seconde), zal het resultaat een cijfer in radialen per seconde zijn, bekend als de hoeksnelheid van het wisselstroomsysteem.
hoeksnelheid in wisselstroomsystemen
hoeksnelheid kan worden weergegeven door de uitdrukking 2nf, of het kan worden weergegeven door zijn eigen symbool, de kleine Griekse letter omega, die lijkt op onze Romeinse kleine letter “W”: ω., De reactantieformule XL = 2nfL kan dus ook worden geschreven als XL = wL.
men moet begrijpen dat deze “hoeksnelheid” een uitdrukking is van hoe snel de WISSELSTROOMGOLFVORMEN cirkelen, waarbij een volledige cyclus gelijk is aan 2π radialen. Het is niet noodzakelijk representatief voor de werkelijke assnelheid van de alternator die de wisselstroom produceert.
indien de alternator meer dan twee polen heeft, is de hoeksnelheid een veelvoud van de assnelheid., Om deze reden wordt ω soms uitgedrukt in eenheden van elektrische radialen per seconde in plaats van (gewone) radialen per seconde, om het te onderscheiden van mechanische beweging.
hoe we ook de hoeksnelheid van het systeem uitdrukken, het is duidelijk dat deze recht evenredig is met de reactantie in een inductor. Als de frequentie (of alternator as snelheid) wordt verhoogd in een AC-systeem, zal een inductor bieden meer weerstand tegen de passage van de stroom, en vice versa.,
wisselstroom in een enkel inductief circuit is gelijk aan de spanning (in volt) gedeeld door de inductieve reactantie (in ohm), net zoals wisselstroom of gelijkstroom in een enkel resistief circuit gelijk is aan de spanning (in volt) gedeeld door de weerstand (in ohm). Een voorbeeldcircuit wordt hier getoond:

inductieve reactantie

Fasehoeken
We moeten echter in gedachten houden dat spanning en stroom niet in fase zijn hier., Zoals eerder werd aangetoond, heeft de spanning een faseverschuiving van + 90° ten opzichte van de stroom. Als we deze fasehoeken van spanning en stroom wiskundig weergeven in de vorm van complexe getallen, dan vinden we dat de oppositie van een inductor tegen stroom ook een fasehoek heeft:


stroom vertraagt spanning met 90° in een inductor.
wiskundig zeggen we dat de fasehoek van de oppositie van een inductor tegen stroom 90° is, wat betekent dat de oppositie van een inductor tegen stroom een positieve imaginaire grootheid is., Deze fasehoek van reactieve oppositie tegen stroom wordt van cruciaal belang in kringsanalyse, vooral voor complexe AC-circuits waar reactantie en weerstand op elkaar inwerken.
het zal nuttig zijn om de oppositie van een component tegen stroom te vertegenwoordigen in termen van complexe getallen in plaats van scalaire hoeveelheden van weerstand en reactantie.
overzicht:
- inductieve reactantie is de weerstand die een inductor biedt tegen wisselstroom vanwege de fase-verschoven opslag en afgifte van energie in zijn magnetisch veld., Reactantie wordt gesymboliseerd door de hoofdletter “X” en wordt gemeten in ohm net als weerstand (R).
- inductieve reactantie kan worden berekend met behulp van deze formule: XL = 2nfL
- de hoeksnelheid van een WISSELSTROOMKRING is een andere manier om zijn frequentie uit te drukken, in eenheden van elektrische radialen per seconde in plaats van cycli per seconde. Het wordt gesymboliseerd door de kleine Griekse letter “Omega,” Of ω.
- inductieve reactantie neemt toe met toenemende frequentie. Met andere woorden, hoe hoger de frequentie, hoe meer het tegen de AC stroom van elektronen.,
gerelateerde werkbladen:
- werkblad voor inductoren
- werkblad voor inductieve reactantie