Varians er et mål for hvor langt et sett av data er spredt ut. Et avvik på null indikerer at alle dataene er identiske. Alle ikke-null avvik er positive.

En liten varians indikerer at data poeng tendens til å være svært nær gjennomsnittet, og til hverandre., En høy varians indikerer at data poeng er svært spredt seg ut fra gjennomsnittet, og fra hverandre. Avvik er gjennomsnittet av de kvadrerte avstander fra hvert punkt til mener.

prosessen med å finne variansen er svært lik for å finne den GALE, gjennomsnittlig absolutt avvik.
Den eneste forskjellen er kvadrering av avstander.
Prosess: (1) Finn det betyr (i gjennomsnitt) på settet. (2) Trekke hver data verdien fra den betyr å finne sin avstand fra gjennomsnittet. (3) Square alle avstander. (4) Legg til alle kvadratene av avstander., (4) Divideres med antall biter av data (for befolkningen varians).

Ett problem med avvik er at den ikke har den samme måleenhet som de opprinnelige dataene. For eksempel, originale data som inneholder lengder målt i fot har en varians målt i kvadratmeter.,

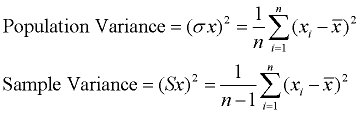Don’t ROUND too soon! When working with the formulas for variance and standard deviation, be careful to avoid rounding too soon., Hvis beregne for hånd, må du alltid ta med deg flere desimaler i beregningene enn det som er forventet for det endelige resultatet. Hvis du arbeider med en kalkulator, bærer den fulle verdien av kalkulator bidrag til du kommer til det endelige resultatet.

standardavvik viser hvor mye variasjon (spredning, spredning, scatter) fra bety eksisterer., Det representerer en «typisk» avvik fra gjennomsnittet. Det er et populært mål på variasjon fordi det går tilbake til den opprinnelige måleenhet av datasettet.

Et lavt standardavvik betyr at data poeng tendens til å være svært nær gjennomsnittet. Et høyt standardavvik tilsier at data punktene er spredt ut over et stort spekter av verdier.
standard avvik kan være tenkt som en «standard» måte å vite hva som er normal (vanlig), det er svært store, og det er svært liten i datasettet.,

standardavvik er et populært mål på variasjon fordi det går tilbake til den opprinnelige måleenhet av datasettet. For eksempel, originale data som inneholder lengder målt i fot har et standardavvik også målt i fot.,

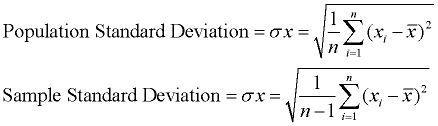for Å beregne standardavvik for hånd:
standard avvik er rett og slett kvadratroten av variansen.
Denne beskrivelsen er for å beregne standardavviket. Hvis utvalgets standardavvik er nødvendig, kan du dele med n – 1 i stedet for n., Siden standardavviket er kvadratroten av variansen, må vi først beregne variansen.
1. Finn de mener.
2. Trekk betyr fra hver dataverdi og torget hver av disse forskjellene (de kvadrerte forskjeller).
3. Finn gjennomsnittet av de kvadrerte forskjeller (legg til dem og dividere med summen av data-verdier). Dette vil være avvik.,

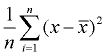varians
4. Ta kvadratroten. Dette vil være standardavviket. Runde svaret i henhold til instruksjonene i problemet.

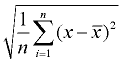standardavvik

Normal Kurve

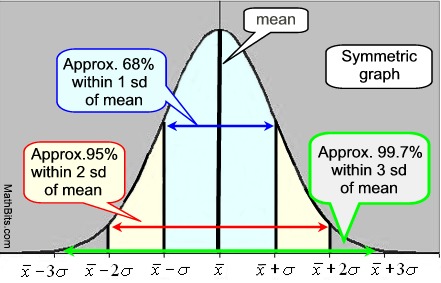
En normal kurve er en symmetrisk, bell-formet kurve., Sentrum av grafen er gjennomsnittlig, og høyden og bredden av grafen er bestemt av standardavvik. Når standardavviket er små, kurven vil være høy og smal i spredning. Når standardavviket er stort, kurven skal være kort og bredt i spredning. Gjennomsnittlig og median har samme verdi i en normal kurve.

Normal Kurve Empiriske Regel:
Ca …

• 68% av de data som ligger innenfor ett standardavvik fra gjennomsnittet.,

• 95% av data ligger innenfor to standardavvik over gjennomsnittet.

• 99.7% av data ligger innenfor tre standardavvik fra gjennomsnittet.

IQR for en normal kurve er 1.34896 x standardavvik.