en Antakelse om normalitet på den avhengige variabelen
The independent t-test krever at den avhengige variabelen er tilnærmet normalfordelt innen hver gruppe.
Merk: Teknisk, det er restene som trenger å være normalfordelt, men for en uavhengig t-test, som begge vil gi deg samme resultat.,
Du kan teste dette ved hjelp av en rekke forskjellige tester, men Shapiro-Wilks test av normalitet eller en grafisk metode, for eksempel et Q-Q-Plott, er svært vanlig. Du kan kjøre disse testene ved hjelp av SPSS Statistikk, prosedyre for, som kan bli funnet i vår Testing for Normalitet guide. Imidlertid, t-testen er beskrevet som en robust test med hensyn til overtakelse av normalitet. Dette betyr at noen avvik bort fra normalitet ikke har en stor innflytelse på Type i feil priser. Unntaket fra dette er hvis forholdet mellom den minste til største gruppen blir større enn 1.,5 (største i forhold til minste).
Hva du skal gjøre når du bryter normalitet forutsetning
Hvis du finner ut at enten en eller begge av dine konsernets data er ikke tilnærmet normalfordelt og grupper størrelser varierer sterkt, har du to alternativer: (1) transform dine data, slik at data blir normalfordelt (for å gjøre dette i SPSS Statistikk se vår guide på å Transformere Data), eller (2) kjører Mann-Whitney U-test, som er en ikke-parametrisk test som ikke krever forutsetning av normalitet (for å kjøre denne testen i SPSS Statistikk se vår guide på Mann-Whitney U-Test).,
Forutsetning av homogenitet i variansen
The independent t-test forutsetter variansen i de to gruppene du måler er like i befolkningen. Hvis avvik er ulik, dette kan påvirke Type i feil. Forutsetningen av homogenitet i variansen kan bli testet ved hjelp av Levene ‘ s Test av Likestilling av Avvik, som er produsert i SPSS Statistikk når du kjører uavhengig t-test prosedyren., Hvis du har kjørt Levene ‘ s Test av Likestilling av Avvik i SPSS Statistikk, vil du få et resultat omtrent som følger:

Denne test for homogenitet i variansen gir en F-statistikk og en betydning verdi (p-verdi). Vi er primært opptatt av den betydning verdi – hvis det er større enn 0.05 (dvs., p > .05), vår gruppe avvik kan bli behandlet som likeverdige. Imidlertid, hvis p < 0.05, vi har ulik avvik og vi har brutt forutsetningen om homogenitet i variansen.,
Overvinne et brudd på forutsetningen om homogenitet i variansen
Hvis Levene ‘ s Test for Likestilling av Avvik er statistisk signifikant, noe som indikerer at gruppen avvik er ulik i befolkningen, kan du rette for dette brudd ved ikke å bruke samlet estimat for feil uttrykket for t-statistikk, men i stedet å bruke en tilpasning til de grader av frihet ved hjelp av Welch-Satterthwaite metode., I alle virkeligheten, vil du sannsynligvis aldri har hørt om disse justeringene fordi SPSS Statistikk skjuler denne informasjonen og bare etiketter som er de to alternativene som «Lik avvik antatt» og «Lik avvik ikke antatt» uten eksplisitt om den underliggende tester som brukes., Men, du kan se bevis på disse testene som nedenfor:
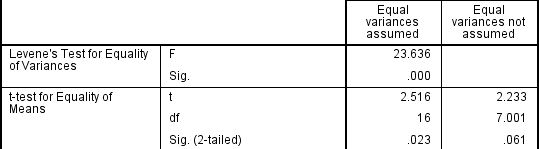
Fra resultatet av Levene ‘ s Test for Likestilling av Avvik, kan vi forkaste nullhypotesen at det ikke er noen forskjell i avvikene mellom grupper og godta den alternative hypotesen at det er en statistisk signifikant forskjell i avvikene mellom grupper., Effekten av å ikke være i stand til å anta lik avvik er tydelig i den siste kolonnen i figuren over, der vi ser en reduksjon i verdien av t-statistikk og en stor reduksjon i frihetsgrader (df). Dette har effekten av å øke p-verdi over kritisk betydning nivå på 0,05. I dette tilfellet, derfor kan vi ikke godta den alternative hypotesen, og akseptere at det er ingen statistisk signifikante forskjeller mellom midler. Dette ville ikke ha vært vår konklusjon hadde vi ikke testet for homogenitet i variansen.