Support Vector Machine eller SVM er en av de mest populære Overvåket Læring algoritmer, som er brukt for Klassifisering, samt Regresjon problemer. Men, først og fremst, det er brukt for Klassifisering problemer i maskinlæring.
målet av SVM-algoritmen er å skape den beste linjen eller beslutning grense som kan skille n-dimensjonale rommet inn i klasser slik at vi kan enkelt sette nye data peker i riktig kategori i fremtiden., Dette best beslutning grensen kalles en hyperplane.
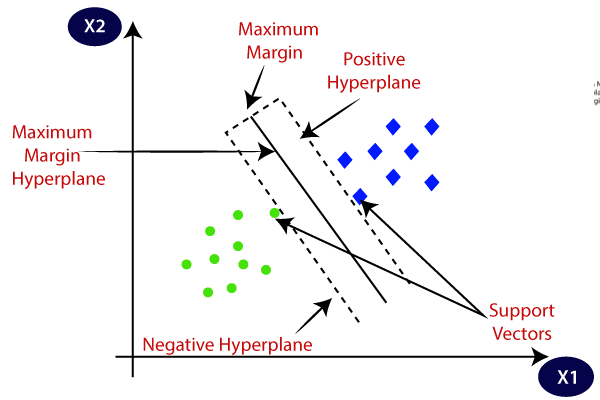
SVM velger ekstreme punkter/vektorer som hjelper til med å skape hyperplane. Disse ekstreme tilfeller er kalt til støtte vektorer, og dermed algoritmen er betegnet som Support Vector Machine. Vurdere nedenfor diagram hvor det er to ulike kategorier som er klassifisert ved hjelp av en beslutning grense eller hyperplane:
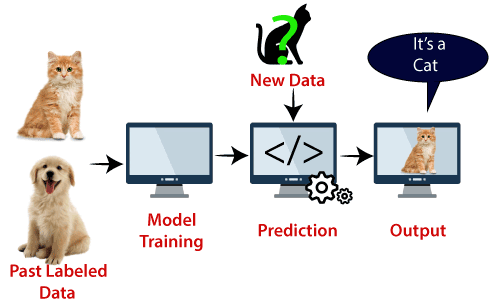
Eksempel: SVM kan forstås med eksempel på at vi har brukt i KNN classifier., Anta at vi ser en merkelig katt som også har noen funksjoner av hunder, så hvis vi ønsker en modell som kan nøyaktig identifisere om det er katt eller hund, så en slik modell kan være opprettet ved hjelp av SVM-algoritmen. Vi vil først tog vår modell med masse bilder av katter og hunder, slik at det kan lære om de ulike funksjoner av katter og hunder, og deretter tester vi det med denne merkelige skapningen. Slik som support vector skaper en beslutning om grensen mellom disse to data (katt og hund) og velge ekstreme tilfeller (støtte vektorer), vil det se den ekstreme tilfelle av katt og hund., På grunnlag av støtte vektorer, det vil klassifisere det som en katt. Vurdere diagrammet nedenfor:
SVM algoritmen kan brukes for ansiktsgjenkjenning, bildestabilisator klassifisering, tekst kategorisering, etc.
Typer SVM
SVM kan være av to typer:
- Lineær SVM: Lineær SVM er brukt for lineært separable data, som betyr at hvis et dataset kan deles inn i to klasser ved hjelp av en enkelt rett linje, så slike data er betegnet som lineært separable data, og classifier brukes som kalles Lineær SVM classifier.,
- Ikke-lineær SVM: Ikke-Lineær SVM er brukt for ikke-lineært atskilt data, som betyr at hvis et dataset som ikke kan klassifiseres ved hjelp av en rett linje, så slike data er betegnet som ikke-lineær data og classifier brukes kalles som Ikke-lineær SVM classifier.
Hyperplane og Støtte Vektorer i SVM algoritme:
Hyperplane: Det kan være flere linjer/vedtak grenser for å skille klassene i n-dimensjonale rommet, men vi må finne ut den beste beslutningen grense som bidrar til å klassifisere data poeng. Dette best grensen er kjent som hyperplane av SVM.,
dimensjonene av hyperplane avhenger av funksjoner som finnes i datasettet, noe som betyr at hvis det er 2 funksjoner (som vist på bildet), deretter hyperplane vil være en rett linje. Og hvis det er 3 funksjoner, så hyperplane vil være en 2-dimensjon flyet.
Vi alltid lage en hyperplane, som har en maksimal margin, noe som betyr at maksimal avstand mellom datapunkter.
Støtte Vektorer:
data-poeng eller vektorer som er nærmest hyperplane og som påvirker plasseringen av hyperplane er betegnet som Støtter Vektor., Siden disse vektorene støtte hyperplane, derfor kalles en Støtte vektor.
Hvordan gjør SVM fungerer?
Lineær SVM:
De som arbeider i SVM algoritmen kan forstås ved hjelp av et eksempel. Anta at vi har et dataset som har to kodene (grønn og blå), og datasettet har to funksjoner x1 og x2. Vi ønsker en classifier som kan klassifisere par(x1, x2) av koordinater i enten grønt eller blått. Vurdere bildet under:
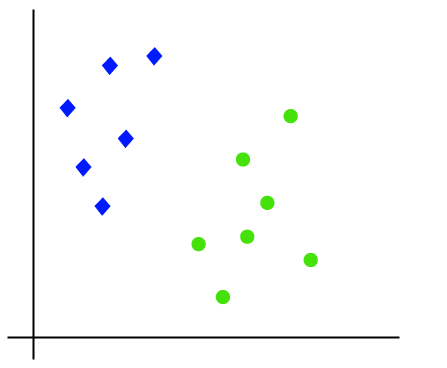
Slik som det er 2-d plass så bare ved hjelp av en rett linje, kan vi lett kan skille disse to klassene., Men det kan være flere linjer som kan skille disse klassene. Vurdere bildet under:
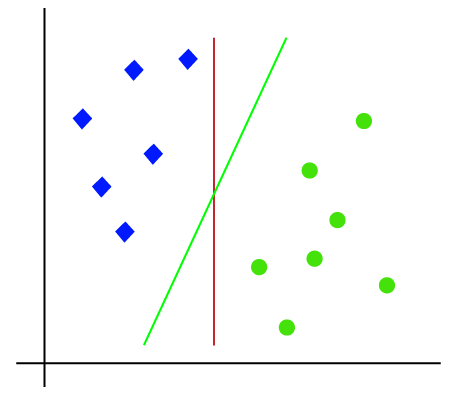
Derfor, SVM algoritme som bidrar til å finne den beste linjen eller beslutning grense; dette best grensen eller område kalles en hyperplane. SVM-algoritmen finner det nærmeste punktet på linjene fra begge klassene. Disse punktene kalles støtte vektorer. Avstanden mellom vektorene og hyperplane er kalt margin. Og målet med SVM er å maksimere dette margin. Den hyperplane med maksimal margin kalles optimal hyperplane.,
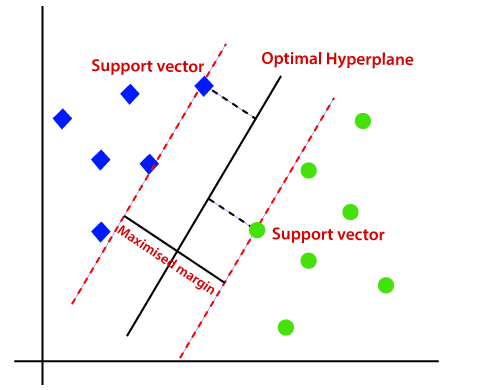
Ikke-Lineær SVM:
Hvis data er lineært ordnet, så vi kan skille det ved hjelp av en rett linje, men for ikke-lineær informasjon, kan vi ikke trekke en eneste rett linje. Vurdere bildet under:
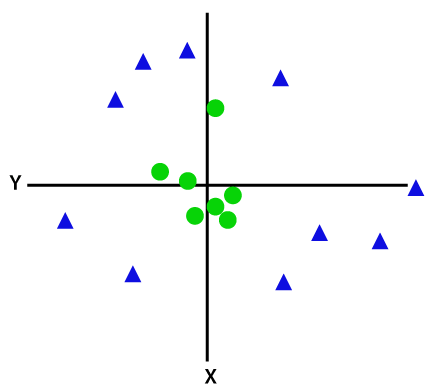
Så for å skille disse data poeng trenger vi for å legge til enda en dimensjon. For lineære data, har vi brukt to dimensjoner x og y, så for ikke-lineære data, vil vi legge til en tredje dimensjon z., Det kan beregnes som:
z=x2 +y2
Ved å legge til en tredje dimensjon, prøven plass vil bli som under bildet:
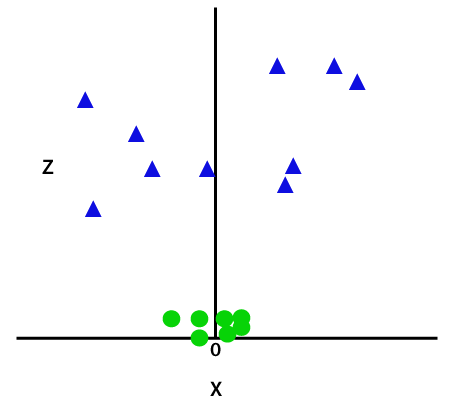
Så nå, SVM vil dele datasett i klasser på følgende måte. Vurdere bildet under:
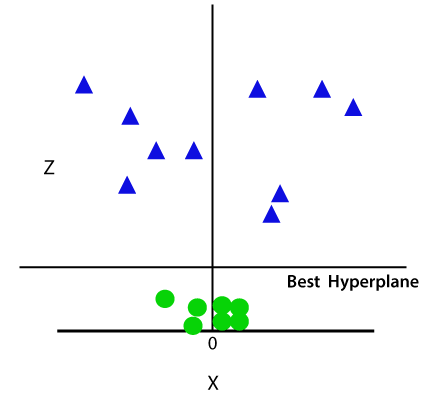
Siden vi er i 3-d Plass, derfor er det så ut som en plan som er parallelt med x-aksen. Hvis vi gjør den i 2d plass med z=1, så vil det bli slik:
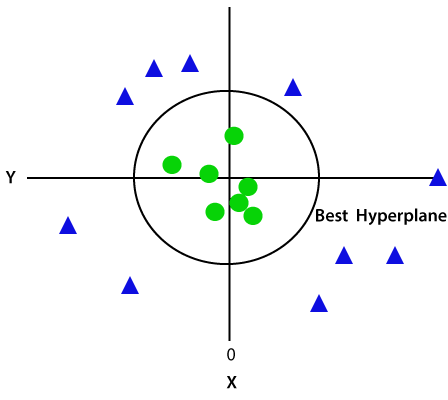
Derfor får vi en omkrets med radius 1 i tilfelle av ikke-lineære data.,
Python Gjennomføring av Support Vector Machine
Nå vil vi gjennomføre SVM-algoritmen ved hjelp av Python. Her vil vi bruke det samme datasettet user_data, som vi har brukt i Logistisk regresjon og KNN klassifisering.
- Data Pre-prosessering trinn
Till Data pre-prosessering trinn, koden vil forbli den samme. Nedenfor er koden:
Etter å ha kjørt koden ovenfor, vil vi pre-behandle data., Koden vil gi datasettet som:
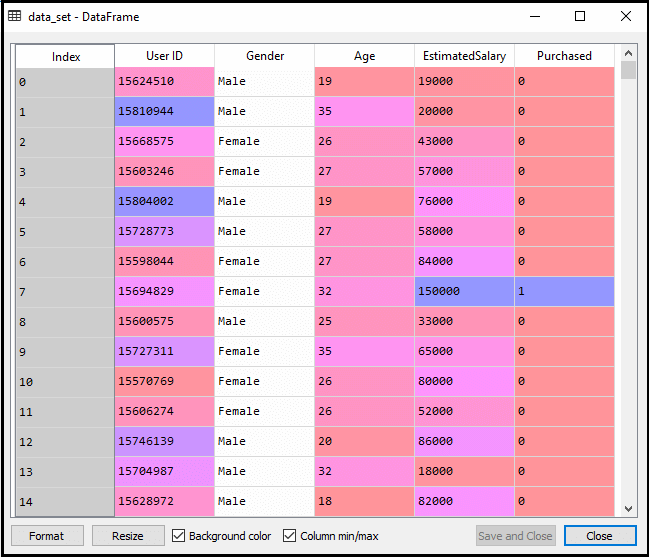
Den graderte utgang for test sett vil være:
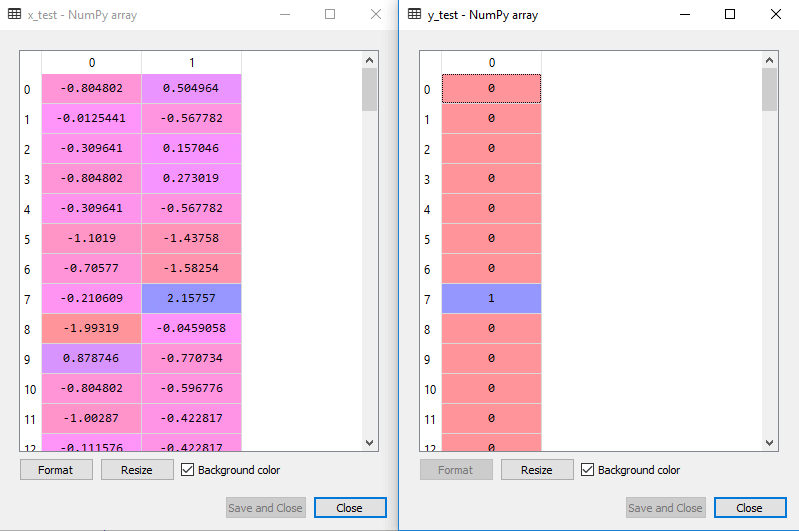
Montering av SVM classifier til trening sett:
Nå er det trening sett vil være tilpasset til SVM classifier. For å opprette SVM classifier, vil vi importere SVC-klasse fra Sklearn.svm bibliotek. Nedenfor er koden for det:
I koden ovenfor, har vi brukt kernel=’lineær’, som her skaper vi SVM for lineært separable data. Men, vi kan endre det for ikke-lineær data., Og da er vi utstyrt den classifier til opplæring dataset(x_train, y_train)
Output:
modellen ytelse kan forandres ved å endre verdien av C(Regularization faktor), gamma, og kjernen.
- Forutsi test satt resultat:
Nå, vi vil forutsi utgang for test sett. For dette, vil vi opprette en ny vektor y_pred. Nedenfor er koden for det:
Etter å ha fått y_pred vektor, kan vi sammenligne resultatet av y_pred og y_test å sjekke forskjellen mellom virkelig verdi og forventet verdi.,
Output: Nedenfor er det utgang for prediksjon av testsettet:

- å Skape forvirring matrise:
Nå vil vi se resultatene av SVM classifier at hvor mange feil spådommer er det i forhold til Logistisk regresjon classifier. For å skape forvirring matrix, trenger vi å importere confusion_matrix funksjon av sklearn bibliotek. Etter import funksjonen, vil vi kalle inn det ved hjelp av en ny variabel cm. Funksjonen tar to parametre, hovedsakelig y_true( faktiske verdier) og y_pred (målrettet verdi retur av classifier)., Nedenfor er koden for det:
Output:
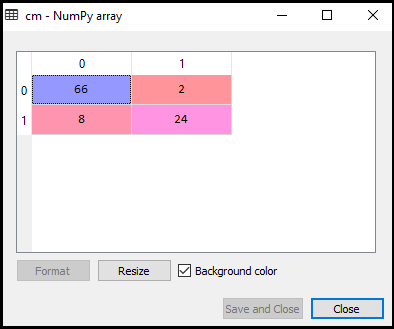
Som vi kan se i over utgang bilde, det er 66+24= 90 riktige spådommer og 8+2= 10 riktige spådommer. Derfor kan vi si at våre SVM modell forbedret i forhold til den Logistiske regresjonsmodellen.,
- Visualisere trening satt resultat:
Nå vil vi visualisere trening satt resultat, nedenfor er koden for det:
Output:
Ved å utføre koden ovenfor, vil vi få den ut som:
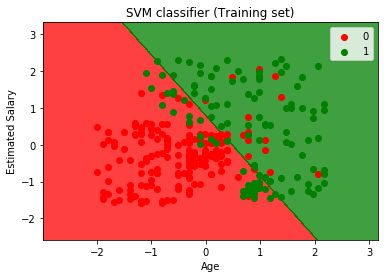
Som vi kan se, ovenfor utgang vises tilsvarende til Logistisk regresjon utgang. I produksjonen, vi fikk rett linje som hyperplane fordi vi har brukt en lineær kjernen i classifier. Og vi har også diskutert ovenfor, som for 2d plass, hyperplane i SVM er en rett linje.,
- Visualisere testsettet resultat:
Output:
Ved å utføre koden ovenfor, vil vi få den ut som:
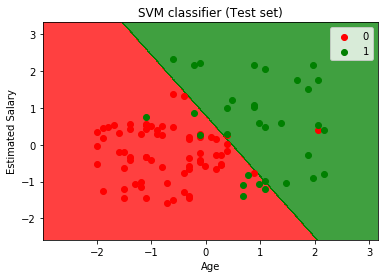
Som vi kan se i over utgang bilde, den SVM classifier har delt inn brukerne i to regioner (som er Kjøpt eller Ikke kjøpt). Brukere som har kjøpt SUV-er i rødt område med røde scatter-poeng. Og brukere som ikke kjøpe SUV-er i det grønne område med grønne scatter-poeng. Den hyperplane har delt opp i to klasser Kjøpt inn og ikke har kjøpt variabel.