Innledning
Lineær regresjon, også kjent som enkel lineær regresjon eller bivariate lineær regresjon brukes når vi ønsker å forutsi verdien på en avhengig variabel basert på verdien av en uavhengig variabel. Du kan For eksempel bruke lineær regresjon for å forstå om eksamen kan ytelsen bli spådd basert på revisjon tid (dvs., din avhengige variabel ville være «eksamen ytelse», målt fra 0-100 merker, og din uavhengige variabelen ville være «revisjon tid», målt i timer). Alternativt, kan du bruke lineær regresjon for å forstå om sigarett forbruk kan forutsies basert på røyking varighet (dvs., din avhengige variabel ville være «sigarett forbruk», målt i form av antall sigaretter konsumert daglig, og din uavhengige variabelen ville være «røyking varighet», målt i dager). Hvis du har to eller flere uavhengige variabler, i stedet for bare en, må du bruke multippel regresjon., Alternativt, hvis du bare ønsker å fastslå om det er en lineær sammenheng finnes, kan du bruke pearsons korrelasjon.
Note: avhengig variabel er også referert til som resultat, mål eller kriteriet variabel, mens den uavhengige variabelen er også referert til som prediktor, forklarende eller regressor variabel. Til syvende og sist, uansett hvilket begrep du bruker, er det best å være konsekvent. Vi vil referere til disse som avhengige og uavhengige variabler i denne håndboken.,
I denne guiden viser vi deg hvordan du utfører lineær regresjon ved hjelp av Stata, samt tolke og rapportere resultatene fra denne testen. Men før vi introdusere deg til denne prosedyren, må du forstå ulike forutsetninger for at dataene må møte for lineær regresjon for å gi deg et gyldig resultat. Vi drøfte disse forutsetningene neste.
Stata
Forutsetninger
Det er syv «forutsetninger» som understøtter lineær regresjon. Hvis noen av disse syv forutsetninger ikke er oppfylt, kan du analysere dine data ved hjelp av lineær fordi du ikke vil få et gyldig resultat., Siden forutsetningene #1 og #2 er knyttet til valg av variabler, de kan ikke bli testet for bruk av Stata. Imidlertid, bør du bestemme deg for om ditt studium oppfyller disse forutsetningene før du går videre.
- Forutsetning #1: Den avhengige variabelen bør være målt på kontinuerlig nivå., Eksempler på slike kontinuerlige variabler inkluderer høyde (målt i fot og tommer), temperatur (målt i oC), lønn (målt i AMERIKANSKE dollar), revisjon tid (målt i timer), intelligensen (målt ved hjelp av IQ-score), reaksjonstid (målt i millisekunder), teste ytelse (målt fra 0 til 100), salg (målt i antall transaksjoner per måned), og så videre. Hvis du er usikker på om din avhengige variabelen er kontinuerlig (dvs., målt på intervall eller forholdet nivå), se våre Typer Variable guide.,
- Forutsetning #2: Den uavhengige variabelen bør være målt på kontinuerlig eller kategoriske nivå. Imidlertid, hvis du har en kategorisk uavhengige variabelen, er det mer vanlig å bruke en uavhengig t-test (for 2 grupper) eller en-veis ANOVA (for 3 grupper eller mer). I tilfelle du er usikker på, eksempler på kategoriske variabler inkluderer kjønn (f.eks., 2 grupper: mannlige og kvinnelige), etnisitet (f.eks, 3 grupper: Europerer, Afrikansk Amerikansk og Spansk), fysisk aktivitet (f.eks., 4 grupper: stillesittende, lav, moderat og høy), og profesjon (f.eks.,, 5 grupper: kirurg, lege, sykepleier, tannlege, terapeut). I denne guiden viser vi deg lineær regresjon prosedyre og Stata-utdata når både avhengige og uavhengige variablene ble målt på en kontinuerlig nivå.
Heldigvis, kan du sjekke forutsetninger #3, #4, #5, #6 og #7 ved hjelp av Stata. Når du flytter på å forutsetninger #3, #4, #5, #6 og #7, vi foreslår at du tester dem i denne rekkefølgen, fordi det representerer en ordre der, hvis et brudd på forutsetningen er ikke rettes opp, vil du ikke lenger være i stand til å bruke lineær regresjon., Faktisk, ikke bli overrasket hvis din data mislykkes ett eller flere av disse forutsetningene siden dette er ganske typisk når du arbeider med reelle data snarere enn lærebok eksempler, som ofte bare vise deg hvordan du utfører lineær regresjon når alt går bra. Likevel, ikke bekymre deg, fordi selv når data mislykkes visse forutsetninger, er det ofte en løsning for å løse dette (f.eks., transformere dataene eller bruke en annen statistisk test i stedet)., Bare husk at hvis du ikke merker at du har data som oppfyller disse forutsetningene eller du teste for dem feil, resultatene du får når du kjører lineær regresjon kan ikke være gyldig.
- Forutsetningen #3: Det må være en lineær sammenheng mellom den avhengige og uavhengige variabler. Mens det er en rekke måter å sjekke om en lineær relasjon eksisterer mellom to variabler, anbefaler vi at du oppretter et scatterplot ved hjelp av Stata, der du kan plotte den avhengige variabelen mot den uavhengige variabelen., Deretter kan du visuelt inspisere scatterplot for å sjekke om linearitet. Din scatterplot kan se ut som noe du ett av følgende:
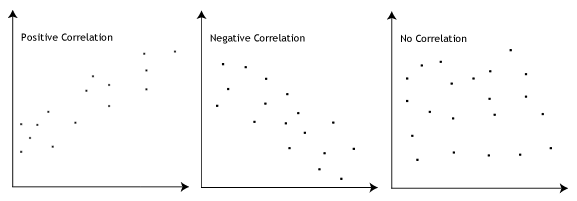
Hvis forholdet vises i din scatterplot er ikke lineær, må du enten kjøre en ikke-lineær regresjonsanalyse eller «transformere» dine data, som du kan gjøre ved hjelp av Stata.
- Forutsetningen #4: Det skal ikke være noen betydelige uteliggere. Uteliggere er rett og slett enkelt data-poeng innenfor data som ikke følger de vanlige mønster (f.eks., i en studie av 100 studenter’ IQ skårer, der gjennomsnittlig score var 108 med bare en liten variasjon mellom studenter, den ene studenten hadde en score på 156, noe som er svært uvanlig, og kan selv sette henne i topp 1% av IQ-score globalt). Følgende scatterplots markere den potensielle effekten av ekstreme verdier:
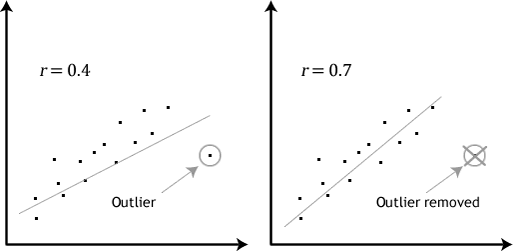
problemet med uteliggere er at de kan ha en negativ effekt på den regresjonsligningen som brukes til å forutsi verdien på den avhengige variabelen basert på den uavhengige variabelen., Dette vil endre utgang som Stata produserer og redusere logisk nøyaktigheten av resultatene. Heldigvis, kan du bruke Stata til å gjennomføre casewise diagnostikk for å hjelpe deg med å oppdage mulige uteliggere.
- Forutsetningen #5: Du bør ha uavhengighet av observasjoner, som du kan enkelt sjekke ved hjelp av Durbin-Watson-statistikken, som er en enkel test for å kjøre ved hjelp av Stata.
- Forutsetningen #6: dataene Dine behov for å vise homoscedasticity, som er der avvik langs den linjen som passer best forbli lignende som du beveger deg langs linjen., De to scatterplots nedenfor gir enkle eksempler på data som oppfyller denne forutsetningen, og en som ikke klarer forutsetning:
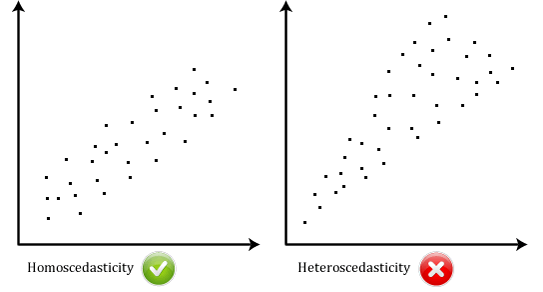
Når du analysere dine egne data, vil du være heldig hvis scatterplot ser ut som en av de to ovenfor. Mens disse bidrar til å illustrere forskjeller i data som oppfyller eller bryter med forutsetningen om homoscedasticity, real-world data er ofte mye mer rotete., Du kan kontrollere om dataene viste homoscedasticity ved å plotte regresjon standardisert restene mot regresjon standardisert forventet verdi.
- Forutsetningen #7: Endelig, må du kontrollere at restene (feil) av regresjons-linje er tilnærmet normalfordelt. To vanlige metoder for å kontrollere denne antakelsen inkluderer bruk av enten et histogram (med en lagt normal kurve) eller en Vanlig P-P-Plott.
I praksis, for å sjekke forutsetninger #3, #4, #5, #6 og #7 vil sannsynligvis ta opp mest mulig ut av din tid ved å gjennomføre lineær regresjon., Imidlertid, det er ikke en vanskelig oppgave, og Stata gir alle verktøyene du trenger for å gjøre dette.
I den delen, Prosedyre, vi illustrere Stata prosedyre som kreves for å utføre lineær regresjon, forutsatt at ingen forutsetninger har blitt brutt. Først setter vi ut eksempelet vi bruker for å forklare lineær regresjon prosedyre i Stata.
Stata
Eksempel
Studier viser at trening kan bidra til å forebygge hjertesykdom. Innenfor rimelighetens grenser, jo mer du trener, jo mindre risiko har du for å lide av hjertesykdom., En måte som trening reduserer risikoen for lider av hjertesykdom ved å redusere fett i blodet ditt, kalt kolesterol. Jo mer du trener, jo lavere kolesterol konsentrasjon. Videre, det har nylig blitt vist at mengden tid du bruker på å se på TV – en indikator på en stillesittende livsstil – kan være en god prediktor for hjerte-og karsykdommer (dvs., som er, jo mer TV du ser, jo større er risikoen for hjertesykdommer).,
Derfor, en forsker bestemte seg for å finne ut om kolesterol konsentrasjon var knyttet til tid brukt på å se på TV i ellers friske 45 til 65 år gamle menn (en på risiko kategori av mennesker). For eksempel, som folk brukte mer tid på å se på TV, gjorde sitt kolesterol konsentrasjon også øke (positivt forhold), eller gjorde det motsatte skje? Forskeren ønsket også å vite andelen av kolesterol konsentrasjon at tid brukt på å se på TV, kunne forklare, så vel som å være i stand til å forutsi kolesterol konsentrasjon., Forskeren kan deretter bestemme om, for eksempel, folk som tilbrakte åtte timer tilbrakt ser på TV per dag hadde faretruende høye nivåer av kolesterol konsentrasjon i forhold til folk ser på bare to timer med TV.
for Å gjennomføre analysen, forsker rekruttert 100 friske mannlige deltakere mellom 45 og 65 år gammel. Mengden av tid brukt på å se på TV (dvs., den uavhengige variabelen, time_tv) og kolesterol konsentrasjon (dvs., avhengig variabel, kolesterol) ble registrert for alle de 100 deltakerne., Uttrykt i variabel form, forsker ønsket å regress kolesterol på time_tv.
Merk: eksempel og data brukt i denne håndboken, er fiktive. Vi har nettopp opprettet dem, for det formål av denne håndboken.
Stata
Oppsett i Stata
Merk: Det spiller ingen rolle om du opprette avhengig eller uavhengig variabel først.
Etter at du har laget disse to variablene – time_tv og kolesterol – vi kom inn i score for hvert inn i to kolonner med Data Editor (Rediger) regneark (dvs., tid i timer som deltakerne så på TV i venstre kolonne (dvs., time_tv, den uavhengige variabelen), og deltakernes kolesterol konsentrasjon i mmol/L i høyre kolonne (dvs., kolesterol, den avhengige variabelen), som vist nedenfor:
Publisert med tillatelse fra StataCorp LP.,
Stata
Test Prosedyre i Stata
I denne seksjonen vil vi vise deg hvordan å analysere dine data ved hjelp av lineær regresjon i Stata når seks forutsetninger i forrige avsnitt, Forutsetninger, har ikke blitt krenket. Du kan utføre lineær regresjon ved hjelp av kode eller Stata er graphical user interface (GUI). Etter at du har utført analysen, kan vi vise deg hvordan du skal tolke resultatene. Først velger du om du ønsker å bruke koden eller Stata er graphical user interface (GUI).,
– Koden
– koden for å utføre lineær regresjon på data tar form:
regress DependentVariable IndependentVariable
Denne koden er tastet inn boksen under:
Publisert med tillatelse fra StataCorp LP.,
ved Hjelp av vårt eksempel der den avhengige variabelen er kolesterol og den uavhengige variabelen er time_tv, den nødvendige koden vil være:
regress kolesterol time_tv
Merk 1: Du trenger for å være presis når du skriver inn koden i safe. Koden er «case sensitive». Hvis du For eksempel inn «Kolesterol» der «C» er store snarere enn små bokstaver (dvs., en liten «c»), som det bør være, vil du få en feilmelding lik følgende:
Merk 2: Hvis du fortsatt får en feilmelding i Note 2: ovenfor, er det verdt å sjekke navnet du ga din to variabler i Data Editor når du setter opp din fil (dvs., se Data Editor-skjermen ovenfor)., I – boksen på høyre side av Data Editor-skjermen, det er slik at du spelt variabler i
– delen, ikke den
– delen for at du må taste inn koden (se nedenfor for vår avhengige variabel). Dette kan virke opplagt, men det er en feil som er noen ganger laget, noe som resulterer i feil i Note 2 ovenfor.
Derfor, taster du inn koden, regress kolesterol time_tv, og trykk på «Return/Enter» – knappen på tastaturet.,
Publisert med tillatelse fra StataCorp LP.
Du kan se Stata-utgang som vil bli produsert her.,
Graphical User Interface (GUI)
De tre trinnene som er nødvendige for å gjennomføre lineær regresjon i Stata 12 og 13 er vist nedenfor:
- Klikk Statistikk > Lineære modeller og relaterte > Lineær regresjon på hovedmenyen, som vist nedenfor:
Publisert med tillatelse fra StataCorp LP.,
Du vil bli presentert med Regress – Lineær regresjon dialog boks:
Publisert med tillatelse fra StataCorp LP.
- Velg kolesterol fra i den Avhengige variabelen: drop-down boks, og time_tv fra den Uavhengige variabler: drop-down boksen. Du vil ende opp med følgende skjermbilde:
Publisert med tillatelse fra StataCorp LP.,
-
Klikk på
– knappen. Dette vil generere utdata.
Stata
Output av lineære regresjonsanalyser i Stata
Hvis dataene gått forutsetning #3 (dvs, det var en lineær sammenheng mellom to variabler), #4 (dvs., det var ingen vesentlige uteliggere), antagelse #5 (dvs., du hadde uavhengighet av observasjonene), antagelse #6 (dvs., data viste homoscedasticity) og forutsetningen #7 (dvs., det rester (feil) var tilnærmet normalfordelt), som vi forklarte tidligere i Forutsetninger delen, vil du bare trenger å tolke følgende lineær regresjon utgang i Stata:
Publisert med tillatelse fra StataCorp LP.,
output består av fire viktige biter av informasjon som: (a) R2-verdien («R-squared» rad) representerer den andelen av variansen i den avhengige variabelen som kan forklares med vår uavhengige variabel (teknisk er den andelen av variasjonen kan forklares med den regresjonsmodell utover de mener modellen). Imidlertid, R2 er basert på prøven og er et positivt skjevt estimat på hvor stor andel av variansen i den avhengige variabelen forklares med den regresjonsmodell (dvs., det er for stor); (b) en justert R2-verdien («Adj R-squared» rad), som korrigerer positiv bias for å gi en verdi som ville være forventet i befolkningen; (c) F-verdi grader av frihet («F( 1, 98)») og statistisk signifikans av regresjonsmodell («Prob > F» rad); og (d) koeffisientene for konstant og uavhengig variabel («Coef.»- kolonnen), som er den informasjonen du trenger for å forutsi den avhengige variabelen, kolesterol, ved hjelp av den uavhengige variabelen, time_tv.
I dette eksempelet, R2 = 0.151. Justert R2 = 0.143 (3 d.s.,), noe som betyr at den uavhengige variabelen, time_tv, forklarer 14.3% av variasjonen i den avhengige variabelen, kolesterol i befolkningen. Justert R2 er også et estimat av effekten størrelse, som på 0.143 (14.3%), er en indikasjon på en middels effektstørrelse, ifølge Cohen ‘ s (1988) klassifisering. Men normalt er det R2 ikke justert R2 som er rapportert i resultatene. I dette eksemplet regresjonsmodell er statistisk signifikante, F(1, 98) = 17.47, p = .0001., Dette viser at totalt sett er den modellen som anvendes, kan statistisk signifikant forutsi den avhengige variabelen, kolesterol.
Merk: Vi presenterer resultatet fra den lineære regresjonsanalyser ovenfor. Men, siden du skulle ha testet dine data for de forutsetninger som vi forklarte tidligere i Forutsetninger delen, vil du også trenger å tolke Stata-utgang som ble produsert når du testet for disse forutsetningene. Dette inkluderer å: (a) scatterplots du brukte for å sjekke om det var en lineær sammenheng mellom to variabler (dvs.,, Forutsetningen #3), (b) casewise diagnostikk for å sjekke det var ingen vesentlige uteliggere (altså, Antakelsen #4); (c) ut fra Durbin-Watson statistikk for å sjekke om uavhengighet av observasjoner (dvs., Forutsetningen #5), (d) et scatterplot av regresjon standardisert restene mot regresjon standardisert forventet verdi for å avgjøre om dataene viste homoscedasticity (altså, Antakelsen #6), og et histogram (sammenliknet med normal kurve) og Normal P-P-Plott for å sjekke om rester (feil) var tilnærmet normalfordelt (altså, Antakelsen #7)., Husk også at hvis dataene ikke klarte noen av disse forutsetninger, utgang som du får fra lineær regresjon prosedyre (dvs., output vi diskutere ovenfor) vil ikke lenger være relevant, og det kan hende du har til å utføre en annen statistisk test for å analysere data.,
Stata
Rapportering utgangen av lineære regresjonsanalyser
Når du rapporterer resultatet av din lineær regresjon, det er god praksis å inkludere: (a) en innledning til analysen du utført; (b) informasjon om prøven, inkludert eventuelle manglende verdier; (c) den observerte F-verdi grader av frihet og betydning nivå (dvs., p-verdi); (d) andelen av variasjonen i den avhengige variabelen forklares av de uavhengige variable (dvs., ditt Justert R2 ); og (e) regresjonsligningen for din modell., Basert på resultatene ovenfor, kan vi rapportere resultatene av denne studien er som følger:
- Generelt
En lineær regresjon etablert som daglig tid brukt på å se på TV kan statistisk signifikant forutsi kolesterol konsentrasjon, F(1, 98) = 17.47, p = .0001 og tid brukt på å se på TV sto for 14.3% av forklart variasjon i kolesterol konsentrasjon. Regresjonsligningen var: spådd kolesterol konsentrasjon = -2.135 + 0.044 x (tid brukt på å se på tv).,
I tillegg til rapportering av resultatene som ovenfor, et diagram kan brukes til visuelt å presentere resultatene. Du kan For eksempel gjøre dette ved hjelp av et scatterplot med tillit og prediksjon intervaller (selv om det ikke er veldig vanlig å legge til den siste). Dette kan gjøre det lettere for andre å forstå resultatene. Videre, du kan bruke den lineære regresjonsligningen til å gjøre forutsigelser om verdien av den avhengige variabelen basert på ulike verdier på den uavhengige variabelen., Mens Stata ikke produsere disse verdiene som en del av lineær regresjon prosedyren over, det er en prosedyre i Stata som du kan bruke til å gjøre det.