Vi klassisk tenke på lys som alltid reiser i rette linjer, men når lys bølger passerer i nærheten av en barriere-de har en tendens til å bøye rundt som barriere og blir spredt ut. Diffraksjon av lys som oppstår når et lys bølge passerer et hjørne eller gjennom en åpning eller slit som er fysisk omtrentlig størrelse, eller enda mindre enn det lyset er på bølgelengde.,

En veldig enkel demonstrasjon av diffraksjon kan bli gjennomført ved å holde hånden foran en lyskilde og sakte lukker to fingre mens du observerer lys overføres mellom dem. Som fingrene nærme hverandre og kommer veldig tett sammen, du begynner å se en serie av mørke linjer parallelt med fingrene. De parallelle linjene er faktisk diffraksjon mønstre. Dette fenomenet kan også oppstå når lyset er «bøyd» rundt partiklene som er i samme størrelsesorden som bølgelengden på lyset., Et godt eksempel på dette er diffraksjon av sollys ved skyer som vi ofte refererer til som en silver lining, som er illustrert i Figur 1 med en vakker solnedgang over havet.
Vi kan ofte observere pastellnyanser i blått, rosa, lilla og grønt i skyer som er generert når lyset er diffracted fra vann dråper i skyer. Mengden av diffraksjon, avhenger av bølgelengden til lys, med kortere bølgelengder blir diffracted på en større vinkel enn lenger de (i kraft, blått og fiolett lys er diffracted på en høyere vinkel enn det som er rødt lys)., Som et lys bølge som reiser gjennom atmosfæren møter en dråpe vann, som vist nedenfor er det først brytes i vann:luft-grensesnitt, så det er ført som det igjen møter grensesnittet. Strålen, fremdeles reiser innenfor vann dråpe, er igjen brytes som det slår grensesnittet for tredje gang. Dette siste interaksjon med grensesnittet, refracts lys tilbake ut i atmosfæren, men det er også diffracts en del av lyset som illustrert nedenfor., Dette diffraksjon element fører til et fenomen som er kjent som Cellini er halo (også kjent som Heiligenschein effekt) hvor en lys ring av lys som omgir shadow of the observer ‘ s head.
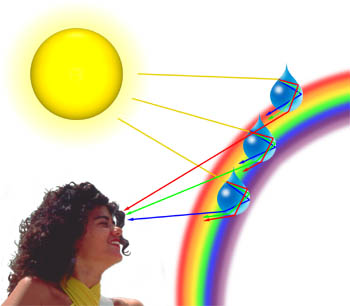
vilkår diffraksjon og spredning brukes ofte om hverandre og er ansett for å være nærmest synonymt. Diffraksjon beskriver en spesialisert tilfelle av lys spredning som et objekt med regelmessig gjenta funksjoner (for eksempel et diffraksjonsgitter) gir en ryddig diffraksjon av lys i en diffraksjon mønster., I den virkelige verden er de fleste objekter er svært kompleks i form og bør anses for å være sammensatt av mange individuelle diffraksjon funksjoner som kan samlet produsere en tilfeldig spredning av lys.
En av de klassiske og mest grunnleggende konsepter som involverer diffraksjon er ett slit optisk diffraksjon eksperiment, først gjennomført i begynnelsen av forrige århundre. Når et lys bølge som forplanter seg gjennom en spalte (eller blenderåpning) resultatet er avhengig av den fysiske størrelsen på blenderåpningen med hensyn til bølgelengden til hendelsen strålen., Dette er illustrert i Figur 3 er forutsatt å ha en helhetlig, monokromatisk bølge som avgis fra kilde S, lik lyset som ville bli produsert ved hjelp av en laser, passerer gjennom blenderåpning d og er diffracted, med den største hendelsen lysstrålen landing på punktet P og den første videregående maxima som oppstår på punktet Q.
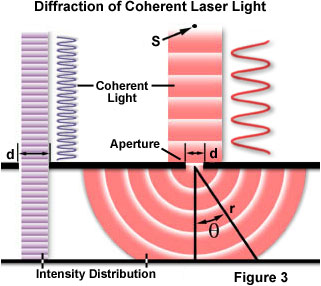
Som vises i venstre side av figuren, når bølgelengden (λ) er mye mindre enn blenderåpning bredde (d), bølgen bare reiser videre i en rett linje, akkurat som den ville gjort hvis det var en partikkel eller ingen aperture var til stede., Imidlertid, når bølgelengden overstiger størrelsen på blenderåpningen, opplever vi diffraksjon av lys i henhold til ligning:
Hvor θ er vinkelen mellom hendelsen sentrale forplantning retning og den første minimum av diffraksjon mønster. Eksperimentet gir en lys og sentral maksimale som er flankert på begge sider av sekundær maxima, med intensiteten av hver påfølgende videregående maksimal synkende etter hvert som avstanden fra sentrum øker. Figur 4 illustrerer dette poenget med en tomt på strålen intensitet versus diffraksjon radius., Vær oppmerksom på at minima som oppstår mellom videregående maxima ligger i multipler av π.
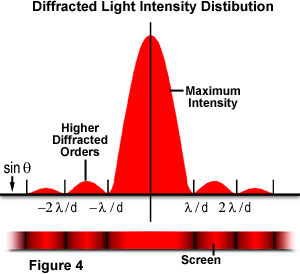
Dette eksperimentet ble først forklart av Augustin Fresnel som sammen med Thomas Young, produsert viktige bevis som bekrefter at lyset går i bølger. Fra tallene ovenfor, ser vi hvordan en helhetlig, monokromatisk lys (i dette eksempel, laser belysning) som slippes ut fra punkt L er diffracted av aperture d., Fresnel antatt at amplituden av den første bestillingen maxima i punktet Q (definert som eQ) vil være gitt ved ligningen:
hvor A er amplituden av hendelsen bølge, r er avstanden mellom d-og Q, og f(χ) er en funksjon av χ, en tilbøyelighet faktor introdusert av Fresnel.
Diffraksjon av Lys
Utforske hvordan en stråle av lys er diffracted når den passerer gjennom en trang åpning eller blenderåpning. Justere bølgelengde og blenderåpning størrelse og observere hvordan dette påvirker diffraksjon intensitet mønster.,
Diffraksjon av lys spiller en viktig rolle i å begrense oppløsningsevne av en optisk instrument (for eksempel: – kameraer, kikkerter, teleskop, mikroskop, og øyet). Oppløsningsevne er den optiske instrument evne til å produsere separate bilder av to tilstøtende poeng. Dette er ofte bestemt av kvaliteten av linser og speil i instrumentet samt egenskapene til det omkringliggende mediet (vanligvis luft). Den bølge-lignende arten av lyset styrker en endelig grense for oppløsningsevne av alle optiske instrumenter.,
Våre diskusjoner av diffraksjon har brukt en spalte som blenderåpning gjennom hvor lyset er diffracted. Imidlertid, alle optiske instrumenter har sirkulær blenderåpning, for eksempel eleven i et øye, eller sirkulær blenderåpning og linser av et mikroskop. Sirkulær blenderåpning produsere diffraksjon mønstre som ligner på de som er beskrevet ovenfor, bortsett fra mønsteret naturlig utstillinger en sirkulær symmetri. Matematisk analyse av diffraksjon mønstre produsert av en sirkulær blenderåpning er beskrevet ved likningen:
hvor θ(1) er vinklet posisjonen til den første bestillingen diffraksjon minima (den første mørke ringen), λ er bølgelengden til hendelsen lys, d er diameteren på blenderåpningen, og 1.22 er en konstant. Under de fleste omstendigheter, vinkelen θ(1) er svært liten, slik tilnærming at synd og tan av vinkelen er nesten lik avkastning:
Fra disse ligningene det blir tydelig at den sentrale maksimum er direkte proporsjonal til λ/d gjør dette til maksimalt mer spredt ut for lengre bølgelengder og for mindre blenderåpninger., Den sekundære mimina av diffraksjon satt en grense for hvor nyttig forstørrelse av objektiv objektiver i optisk mikroskopi, på grunn av iboende diffraksjon i lys av disse objektivene. Uansett hvor perfekt linsen kan være, er det bildet av en kilde av lys produsert av linsen er ledsaget av videregående og høyere for maxima. Dette kan fjernes bare hvis objektivet hadde en uendelig diameter. To objekter atskilt med en avstand mindre enn θ(1) kan ikke løses, uansett hvor høy den makt for forstørrelse., Mens disse ligningene ble hentet for bildet av en kilde av lys i en uendelig avstand fra aperture, det er en rimelig tilnærming av oppløsningsevne av et mikroskop når d er erstatning for de diameter av objektiv.
Derfor, hvis to objekter bor i en avstand D fra hverandre og er i en avstand L fra en observatør, vinkelen (uttrykt i radianer) mellom dem er:
som fører oss til å være i stand til å kombinere de to siste ligningene å gi:
Hvor D(0) er den minste avstanden mellom objekter som vil tillate dem å være løst. Ved hjelp av denne ligningen, det menneskelige øyet kan løse objekter atskilt med en avstand på 0.056 millimeter, men fotoreseptorer i netthinnen er ikke ganske nær nok sammen til at denne graden av oppløsning, og 0,1 millimeter er et mer realistisk tall under normale omstendigheter.
oppløsningsevne av optiske mikroskoper er bestemt av en rekke faktorer, inkludert de som ble diskutert, men i den mest ideelle forhold, dette tallet er ca 0,2 micrometers., Dette nummeret må ta hensyn til optisk justering av mikroskop, kvaliteten på linsene, så vel som den dominerende bølgelengder av lyset som brukes til bilde prøven. Mens det er ofte ikke nødvendig å beregne eksakt oppløsningsevne av hvert mål (og ville være en sløsing med tid i de fleste tilfeller), det er viktig å forstå egenskapene til mikroskopet linser som de gjelder for den virkelige verden.
bidragsytere
Mortimer Abramowitz – Olympus America, Inc. To Corporate Center-Stasjon. Melville, New York, 11747.
Michael W., Davidson – Nasjonale Høyt Magnetisk Felt, Laboratorium, 1800 Øst Paul Dirac Dr., Florida State University, Tallahassee, Florida, 32310.