læringsutbytte
- Identifisere foci, hjørner, økser, og i sentrum av en ellipse.
- Skriv ligninger av ellipser sentrert i origo.
- Skriv ligninger av ellipser ikke er sentrert i origo.
En ikpsoniske delen, eller ikpsoniske, er en form som følge av kryssende en rett sirkulær kjegle med et plan. Den vinkelen som flyet krysser membranen bestemmer formen.,
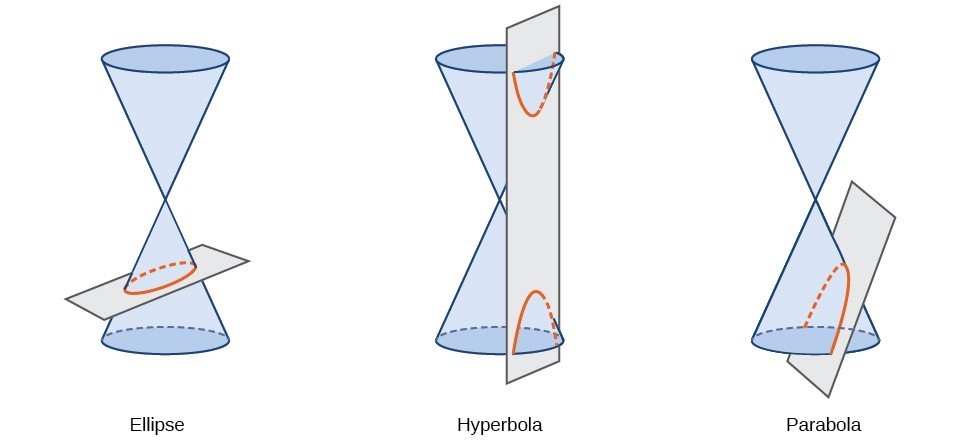
kjeglesnitt kan også beskrives ved et sett av punkter i koordinering-flyet. Senere i dette kapitlet vil vi se at grafen for alle kvadratiske likningen i to variabler er en ikpsoniske delen. Tegn av ligninger og koeffisientene til variablene vilkårene bestemmer formen. Denne delen fokuserer på de fire varianter av standard form av formelen for en ellipse. En ellipse er sett av alle poeng \left(x,y\høyre) i en plan slik at summen av deres avstander i forhold til to faste punkter er en konstant., Hver fast punkt kalles et fokus (flertall: foci) av ellipsen.
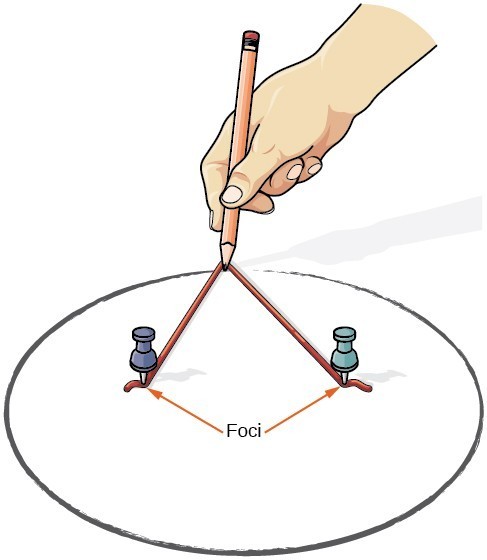
Vi kan tegne en ellipse med et stykke papp, to tegnestifter, en blyant, og string. Plasser tegnestifter i papp for å danne foci av ellipsen. Klipp et stykke streng lenger enn avstanden mellom de to tegnestifter (lengden av strengen representerer den konstante i definisjonen). Tack hver ende av tråden til papp, og spore en kurve med en blyant holdt stram mot strengen. Resultatet er en ellipse.
Hver ellipse har to akser av symmetri., Jo lenger aksen kalles den store aksen, og den kortere aksen kalles mindre aksen. Hvert endepunkt av den store aksen er toppunktet av ellipsen (flertall: hjørner), og hvert endepunkt i mindre aksen er en co-vertex av ellipsen. Sentrum av en ellipse er midtpunktet av både store og små akser. Aksene er vinkelrett på senteret. Foci alltid ligge på den store aksen, og summen av avstandene fra foci til et punkt på ellipsen (konstant sum) er større enn avstanden mellom foci.,
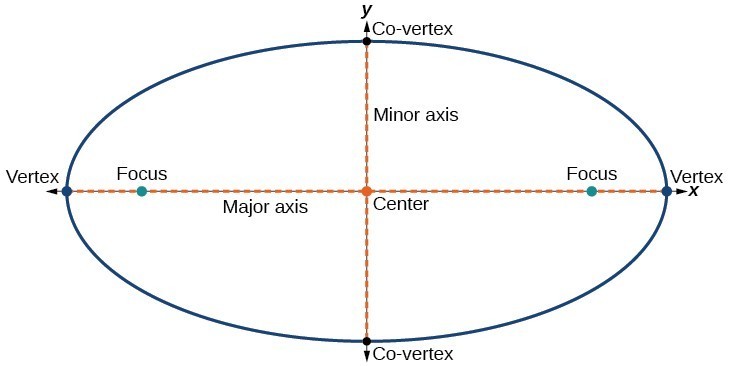
I dette kapitlet skal vi begrense ellipser til de som er plassert vertikalt eller horisontalt i koordinering-flyet. Det er, aksene vil enten ligge på eller være parallell med x– og y-aksene. Senere i kapitlet vil vi se ellipse som er rotert i koordinering-flyet.
for Å arbeide med horisontal og vertikal prikker i koordinering-fly, anser vi to tilfeller: de som er sentrert i origo, og de som er sentrert på et punkt annet enn opprinnelsen., Først vil vi lære å utlede ligninger av ellipser, og da vil vi lære hvordan å skrive den ligninger av prikker i standard form. Senere vil vi bruke det vi lærer å tegne grafer.,v>Hvis (x,y) er et punkt på ellipse, så vi kan definere følgende variabler:
\begin{align}d_1&=\text{avstanden fra } (-c,0) \text{ for } (x,y) \\ d_2&= \text{avstanden fra } (c,0) \text{ for } (x,y) \end{align}
\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1
for en ellipse sentrert i origo med sin store aksen på X-aksen og
\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1
for en ellipse sentrert i origo med sin store aksen på Y-aksen.,
Skrive Ligninger av Ellipser Ikke er Sentrert i origo
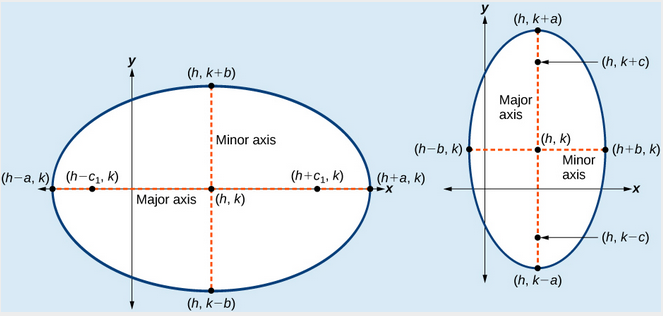
(a) Horisontal ellipse med sentrum \left(h,k\right) (b) Vertikal ellipse med sentrum \left(h,k\right)
Løse Anvendte Problemer som Involverer Ellipser
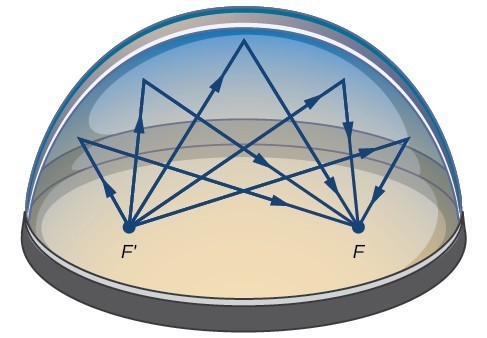
Mange virkelige situasjoner kan være representert ved ellipser, inkludert banene til planetene, satellitter, måner og kometer, og former av båt kjøl, ror, og noen flyvinger. En medisinsk enhet som kalles en lithotripter bruker elliptiske reflektorer for å bryte opp nyre steiner ved genererer lydbølger., Noen bygninger, kalt hvisker chambers, er utformet med elliptisk kupler, slik at en person som hvisker i ett fokus kan lett bli hørt av noen som står på den andre fokus. Dette skjer på grunn av de akustiske egenskapene til en ellipse. Når en lydbølge utspring på ett fokus for en hviskende kammer, lydbølge vil bli reflektert av den elliptiske dome og tilbake til den andre fokus. I den stille kammer på Museum of Science and Industry i Chicago, to personer som står ved foci—ca 43 meter fra hverandre—kan høre hverandre hviske.