Dette er den første i en tre-post-serien. Andre innlegget snakker abouthow å beregne Stor-O. Den tredje artikkelen handler om understandingthe formell definisjon av Stor-O.
Big-O notasjon som brukes til å være en veldig skremmende konsept for meg. Jeg thoughtthis er hvordan «ekte» programmerere snakket om sin kode. Det var alle themore skremmende fordi den akademiske beskrivelser (som Wikipedia) madevery lite mening for meg. Dette er frustrerende fordi underlyingconcepts er faktisk ikke så vanskelig.,
Enkelt sagt, Big-O notasjon er hvordan programmerere snakke aboutalgorithms. Algoritmer er en annen skremmende tema som jeg vil dekke inanother innlegg, men for vårt formål, la oss si at «algoritme» betyr afunction i programmet (som ikke er for langt unna). En funksjon er Stor-Onotation bestemmes av hvordan den reagerer på ulike innganger. Howmuch tregere er det hvis vi gir det en liste over 1000 ting til å fungere oninstead av en liste med 1 ting?
bør du Vurdere denne koden:
def item_in_list(to_check, the_list): for item in the_list: if to_check == item: return True return False
Så hvis vi kaller denne funksjonen som item_in_list(2, ), det shouldbe ganske raskt., Vi loop over hver ting i listen, og hvis vi findthe første argumentet til vår funksjon, returnere True. Hvis vi får til endand vi fant du ikke det, returnere False.
«kompleksitet» av denne funksjonen er O(n). Jeg vil forklare hva thismeans i bare et sekund, men la oss bryte ned denne mathematicalsyntax. O(n) leses «For N» fordi O funksjon er alsoknown som For funksjonen. Jeg tror dette er fordi vi er doingapproximation, som hotelltilbud i «størrelsesordener».,
«størrelsesordener» er ENDA et matematisk uttrykk whichbasically forteller forskjellen mellom klasser av tall. Tror thedifference mellom 10 og 100. Hvis du bilde 10 av dine closestfriends og 100 personer, og det er en veldig stor forskjell. På samme måte, thedifference mellom 1 000 og 10 000 er ganske stor (faktisk, sin thedifference mellom en junker bil og en lett brukt en). Det viser outthat i tilnærming, så lenge du er innenfor en størrelsesorden,er du ganske nær., Hvis du skulle gjette antall gumballs i amachine, vil du være i en størrelsesorden hvis du sa 200gumballs. 10,000 gumballs ville være MÅTE på.

Figur 1: En gumball maskin som antall gumballs er sannsynligvis i en størrelsesorden på 200.
Tilbake til å dissekere O(n), denne sier at hvis vi skulle tegne en graf av den timeit tar å kjøre denne funksjonen med ulik størrelse innganger (f.eks. anarray av 1 element 2 elementer 3 elementer, etc), vil vi se at itapproximately tilsvarer antall elementer i tabellen., Dette kalt en lineær graf. Dette betyr at linjen er i utgangspunktet straightif du var å tegne den.
Noen av dere har kanskje fanget at hvis i kode-eksempel ovenfor, ouritem var alltid det første elementet i listen, for vår-kode vil bli reallyfast! Dette er sant, men Big-O er alt om den omtrentlige verste-caseperformance å gjøre noe. Verste fall hvis du ikke har koden ovenfor isthat det ting vi leter etter, ikke er på listen i det hele tatt. (Merk:Det matematiske uttrykket for dette er «øvre grense», noe som betyr at du snakker aboutthe matematiske grense på awfulness).,
Hvis du ønsker å se en graf for disse funksjonene, kan du ignorere O()funksjon og endre variabelen n for x. Du kan deretter skriver du inn thatinto Wolfram Alpha som «tomt x» som vil vise deg en diagonalline. Grunnen til at du bytt ut n for x er som sine grafiske programwants x som variabel navn fordi det svarer til xaxis. X-aksen blir større fra venstre til høyre tilsvarer togiving større og større matriser til funksjonen din., Y-axisrepresents tid, så jo høyere linjen, jo tregere den er.
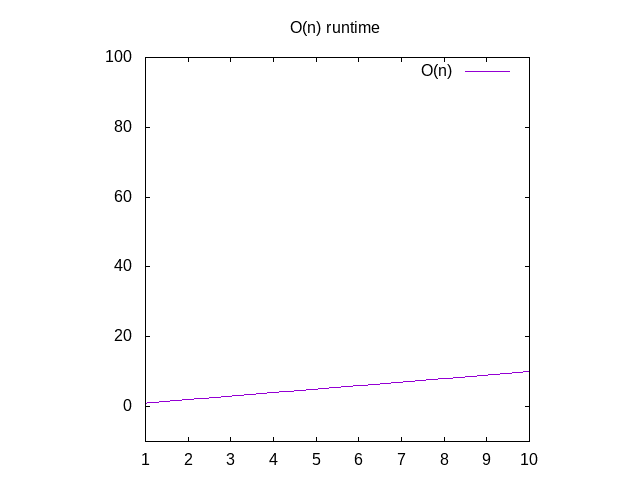
Figur 2: Runtime egenskaper av en O(n) funksjon
Så hva er noen andre eksempler på dette?
bør du Vurdere denne funksjonen:
def is_none(item): return item is None
Dette er en bit av et idiotisk eksempel, men bær over med meg. Denne funksjonen kalt O(1) som er kalt «konstant tid». Hva dette betyr er nomatter hvor stor vår inngang er, det tar alltid samme mengde timeto beregne ting., Hvis du vil gå tilbake til Wolfram og plot 1, vil du seethat det alltid forblir den samme, uansett hvor langt til høyre vi går. Hvis youpass i en liste over 1 million heltall, det vil ta omtrent samme timeas hvis du skulle passere i en liste over 1 heltall. Konstant tid isconsidered den best case scenario for en funksjon.
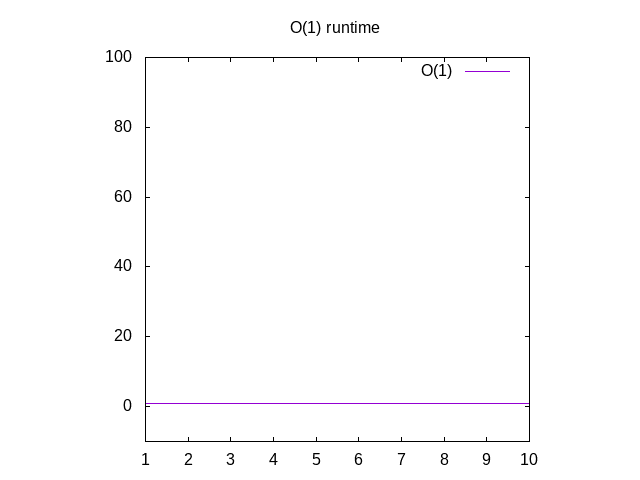
Figur 3: Runtime egenskaper av en O(1) funksjon
bør du Vurdere denne funksjonen:
Nedenfor er en sammenligning av hver av disse grafene, for referanse., Du kan se at en O(n^2) funksjon vil få treg veldig raskt hvor som noe som opererer i konstant tid vil være mye bedre. Dette er spesielt nyttig når det kommer til data strukturer, som jeg skal legge om snart.
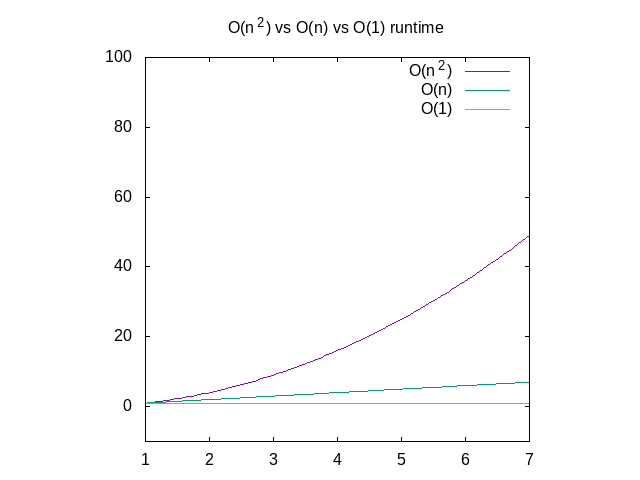
Figur 4: Sammenligning av O(n2) vs O(n) vs O(1) funksjoner
Dette er et ganske høyt nivå oversikt over Big-O notasjon, men hopefullygets du kjent med emnet., Det er en coursera kurs whichcan gi deg en dypere innsikt i dette emnet, men vær advart thatit vil hoppe inn i matematisk notasjon svært raskt. Hvis det er noe som her ikke gir mening, send meg en e-post.
Oppdatering: jeg har også skrevet om hvordan beregne med Stor O.
jeg tenker på å skrive en bok om dette emnet. Hvis dette er somethingyou ønsker å se, vennligst uttrykke din interesse i det her.