Einführung
Lineare Regression, auch als einfache lineare Regression oder bivariate lineare Regression bekannt, wird verwendet, wenn wir den Wert einer abhängigen Variablen basierend auf dem Wert einer unabhängigen Variablen vorhersagen möchten. Sie können beispielsweise die lineare Regression verwenden, um zu verstehen, ob die Prüfungsleistung basierend auf der Revisionszeit vorhergesagt werden kann (dh,, ihre abhängige Variable wäre „Prüfungsleistung“, gemessen von 0-100 Mark, und Ihre unabhängige Variable wäre“ Revisionszeit“, gemessen in Stunden). Alternativ können Sie eine lineare Regression verwenden, um zu verstehen, ob der Zigarettenkonsum basierend auf der Rauchdauer vorhergesagt werden kann (dh Ihre abhängige Variable wäre „Zigarettenkonsum“, gemessen anhand der Anzahl der täglich konsumierten Zigaretten, und Ihre unabhängige Variable wäre „Rauchdauer“, gemessen in Tagen). Wenn Sie zwei oder mehr unabhängige Variablen anstelle von nur einer haben, müssen Sie mehrere Regressionen verwenden., Wenn Sie nur feststellen möchten, ob eine lineare Beziehung besteht, können Sie alternativ die Pearson-Korrelation verwenden.
Hinweis: Die abhängige Variable wird auch als Ergebnis -, Ziel-oder Kriteriumsvariable bezeichnet, während die unabhängige Variable auch als Prädiktor -, Erklärungs-oder Regressorvariable bezeichnet wird. Letztendlich ist es am besten, konsistent zu sein, unabhängig davon, welchen Begriff Sie verwenden. Wir werden diese in diesem Handbuch als abhängige und unabhängige Variablen bezeichnen.,
In diesem Handbuch zeigen wir Ihnen, wie Sie eine lineare Regression mit Stata durchführen und die Ergebnisse dieses Tests interpretieren und melden. Bevor wir Ihnen dieses Verfahren vorstellen, müssen Sie jedoch die verschiedenen Annahmen verstehen, die Ihre Daten erfüllen müssen, damit die lineare Regression ein gültiges Ergebnis liefert. Wir diskutieren diese Annahmen als nächstes.
Stata
Annahmen
Es gibt sieben „Annahmen“, die die lineare Regression untermauern. Wenn eine dieser sieben Annahmen nicht erfüllt ist, können Sie Ihre Daten nicht mit linear analysieren, da Sie kein gültiges Ergebnis erhalten., Da sich die Annahmen #1 und #2 auf Ihre Variablenauswahl beziehen, können sie nicht auf die Verwendung von Stata getestet werden. Sie sollten jedoch entscheiden, ob Ihre Studie diese Annahmen erfüllt, bevor Sie fortfahren.
- Annahme #1: Ihre abhängige Variable sollte auf der kontinuierlichen Ebene gemessen werden., Beispiele für solche kontinuierlichen Variablen sind Höhe (gemessen in Fuß und Zoll), Temperatur (gemessen in oC), Gehalt (gemessen in US-Dollar), Revisionszeit (gemessen in Stunden), Intelligenz (gemessen mit IQ-Score), Reaktionszeit (gemessen in Millisekunden), Testleistung (gemessen von 0 bis 100), Umsatz (gemessen in Anzahl der Transaktionen pro Monat) und so weiter. Wenn Sie sich nicht sicher sind, ob Ihre abhängige Variable kontinuierlich ist (dh auf Intervall-oder Verhältnisebene gemessen wird), lesen Sie unseren Variablentyp-Leitfaden.,
- Annahme #2: Ihre unabhängige Variable sollte auf kontinuierlicher oder kategorialer Ebene gemessen werden. Wenn Sie jedoch eine kategoriale unabhängige Variable haben, ist es üblicher, einen unabhängigen t-Test (für 2 Gruppen) oder eine Einweg-ANOVA (für 3 Gruppen oder mehr) zu verwenden. Falls Sie sich nicht sicher sind, umfassen Beispiele für kategoriale Variablen Geschlecht (z. B. 2 Gruppen: männlich und weiblich), ethnische Zugehörigkeit (z. B. 3 Gruppen: Kaukasisch, afroamerikanisch und hispanisch), körperliche Aktivität (z. B. 4 Gruppen: sesshaft, niedrig, mittel und hoch) und Beruf (z.,, 5 Gruppen: Chirurg, Arzt, Krankenschwester, Zahnarzt, Therapeut). In diesem Handbuch zeigen wir Ihnen das lineare Regressionsverfahren und die Stata-Ausgabe, wenn sowohl Ihre abhängigen als auch unabhängige Variablen auf einer kontinuierlichen Ebene gemessen wurden.
Glücklicherweise können Sie Annahmen überprüfen #3, #4, #5, #6 und #7 mit Stata. Beim Übergang zu Annahmen #3, #4, #5, #6 und # 7 empfehlen wir, sie in dieser Reihenfolge zu testen, da sie eine Reihenfolge darstellt, in der Sie keine lineare Regression mehr verwenden können, wenn eine Verletzung der Annahme nicht korrigierbar ist., Seien Sie in der Tat nicht überrascht, wenn Ihre Daten eine oder mehrere dieser Annahmen nicht erfüllen, da dies eher typisch für die Arbeit mit realen Daten als für Lehrbuchbeispiele ist, die Ihnen oft nur zeigen, wie Sie eine lineare Regression durchführen, wenn alles gut läuft. Machen Sie sich jedoch keine Sorgen, denn selbst wenn Ihre Daten bestimmte Annahmen nicht erfüllen, gibt es häufig eine Lösung, um dies zu überwinden (z. B. Transformieren Sie Ihre Daten oder verwenden Sie stattdessen einen anderen statistischen Test)., Denken Sie daran, dass die Ergebnisse, die Sie beim Ausführen der linearen Regression erhalten, möglicherweise nicht gültig sind, wenn Sie nicht überprüfen, ob Ihre Daten diesen Annahmen entsprechen oder falsch darauf testen.
- Annahme #3: Es muss eine lineare Beziehung zwischen abhängigen und unabhängigen Variablen. Es gibt zwar eine Reihe von Möglichkeiten zu überprüfen, ob eine lineare Beziehung zwischen Ihren beiden Variablen besteht, Wir empfehlen jedoch, ein Scatterplot mit Stata zu erstellen, in dem Sie die abhängige Variable anhand Ihrer unabhängigen Variablen darstellen können., Sie können dann das Scatterplot visuell untersuchen, um die Linearität zu überprüfen. Ihr Scatterplot sieht möglicherweise wie folgt aus:
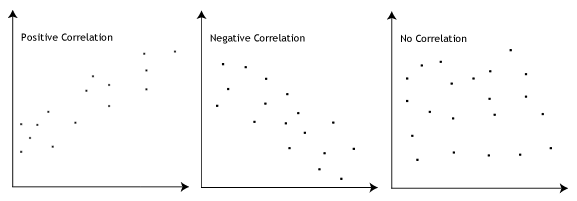
Wenn die in Ihrem Scatterplot angezeigte Beziehung nicht linear ist, müssen Sie entweder eine nichtlineare Regressionsanalyse durchführen oder Ihre Daten“ transformieren“, was Sie mit Stata tun können.
- Annahme #4: Es sollte keine signifikanten Ausreißer. Ausreißer sind einfach einzelne Datenpunkte innerhalb Ihrer Daten, die nicht dem üblichen Muster folgen (z., in einer Studie von 100 Studierenden der IQ-Werte, wobei der Mittelwert war 108 nur mit einer kleinen variation zwischen die Schüler, ein student hatte eine Punktzahl von 156, was sehr ungewöhnlich ist, und können sogar legte Sie in den top 1% der IQ-Werte weltweit). Die folgenden Scatterplots heben die möglichen Auswirkungen von Ausreißern hervor:
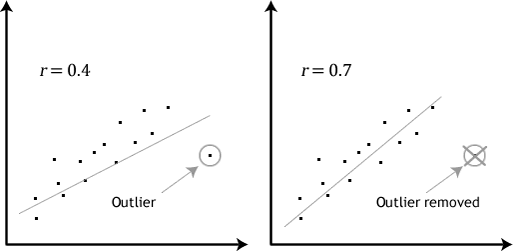
Das Problem mit Ausreißern besteht darin, dass sie sich negativ auf die Regressionsgleichung auswirken können, die verwendet wird, um den Wert der abhängigen Variablen basierend auf der unabhängigen Variablen vorherzusagen., Dadurch wird die von Stata erzeugte Ausgabe geändert und die Vorhersagegenauigkeit Ihrer Ergebnisse verringert. Glücklicherweise können Sie Stata verwenden, um eine Casewise-Diagnose durchzuführen, um mögliche Ausreißer zu erkennen.
- Annahme #5: Sie sollten Unabhängigkeit von Beobachtungen haben, die Sie leicht mit der Durbin-Watson-Statistik überprüfen können, die ein einfacher Test ist, der mit Stata ausgeführt wird.
- Annahme #6: Ihre Daten müssen Homoskedastizität zeigen, wobei die Varianzen entlang der Linie der besten Anpassung ähnlich bleiben, wenn Sie sich entlang der Linie bewegen., Die beiden folgenden Scatterplots bieten einfache Beispiele für Daten, die dieser Annahme entsprechen, und eine, die die Annahme nicht erfüllt:
Wenn Sie Ihre eigenen Daten analysieren, haben Sie Glück, wenn Ihr Scatterplot wie einer der beiden oben genannten aussieht. Während diese helfen, die Unterschiede in den Daten zu veranschaulichen, die die Annahme der Homosexualität erfüllen oder verletzen, sind reale Daten oft viel chaotischer., Sie können überprüfen, ob Ihre Daten Homoskedastizität zeigten, indem Sie die Regressions-standardisierten Residuen gegen den Regressions-standardisierten vorhergesagten Wert plotten.
- Annahme # 7: Schließlich müssen Sie überprüfen, ob die Residuen (Fehler) der Regressionslinie ungefähr normal verteilt sind. Zwei gängige Methoden zur Überprüfung dieser Annahme umfassen entweder die Verwendung eines Histogramms (mit einer überlagerten Normalkurve) oder eines normalen P-P-Diagramms.
In der Praxis auf Annahmen prüfen#3, #4, #5, #6 und #7 wird wahrscheinlich die meiste Zeit in Anspruch nehmen, wenn Sie eine lineare Regression durchführen., Es ist jedoch keine schwierige Aufgabe, und Stata bietet alle Tools, die Sie dazu benötigen.
Im Abschnitt Prozedur veranschaulichen wir die Stata-Prozedur, die für die lineare Regression erforderlich ist, sofern keine Annahmen verletzt wurden. Zunächst legen wir das Beispiel dar, mit dem wir das lineare Regressionsverfahren in Stata erklären.
Stata
Beispiel
Studien zeigen, dass Sport dazu beitragen kann, Herzerkrankungen vorzubeugen. Je mehr Sie in vernünftigen Grenzen trainieren, desto geringer ist das Risiko, an Herzerkrankungen zu leiden., Eine Möglichkeit, das Risiko für Herzerkrankungen durch Bewegung zu senken, besteht darin, ein Fett im Blut, das Cholesterin genannt wird, zu reduzieren. Je mehr Sie trainieren, desto niedriger ist Ihre Cholesterinkonzentration. Darüber hinaus wurde kürzlich gezeigt, dass die Zeit, die Sie mit dem Fernsehen verbringen – ein Indikator für eine sitzende Lebensweise – ein guter Prädiktor für Herzerkrankungen sein kann (dh je mehr fernsehen Sie sehen, desto größer ist Ihr Risiko für Herzerkrankungen).,
Daher beschloss ein Forscher zu bestimmen, ob die Cholesterinkonzentration mit der Fernsehzeit bei ansonsten gesunden 45-bis 65-jährigen Männern (einer Risikokategorie von Personen) zusammenhängt. Zum Beispiel, als die Leute mehr Zeit damit verbrachten, fernzusehen, nahm auch ihre Cholesterinkonzentration zu (eine positive Beziehung); oder ist das Gegenteil passiert? Der Forscher wollte auch den Anteil der Cholesterinkonzentration wissen, den die Fernsehzeit erklären und die Cholesterinkonzentration vorhersagen kann., Der Forscher konnte dann feststellen, ob beispielsweise Menschen, die acht Stunden lang pro Tag ferngesehen haben, im Vergleich zu Menschen, die nur zwei Stunden ferngesehen haben, eine gefährlich hohe Cholesterinkonzentration aufwiesen.
Zur Durchführung der Analyse rekrutierte der Forscher 100 gesunde männliche Teilnehmer im Alter zwischen 45 und 65 Jahren. Die Zeitdauer, die für Fernsehen (D. H., die unabhängige variable, time_tv) und Cholesterin-Konzentration (D. H., die abhängige variable, Cholesterin) wurden für alle 100 Teilnehmer., In variablen Begriffen ausgedrückt, wollte der Forscher Cholesterin auf time_tv zurückbilden.
Hinweis: Das für dieses Handbuch verwendete Beispiel und die Daten sind fiktiv. Wir haben sie gerade für die Zwecke dieses Handbuchs erstellt.
Stata
Setup in Stata
Hinweis: Es spielt keine Rolle, egal, ob Sie abhängige oder unabhängige variable zuerst.
Nach dem Erstellen dieser beiden Variablen-time_tv und Cholesterin-haben wir die Ergebnisse für jede in die beiden Spalten der Dateneditor-Tabelle (Edit) eingegeben (dh,, die Zeit in Stunden, die die Teilnehmer in der linken Spalte fernsahen (dh time_tv, die unabhängige Variable), und die Cholesterinkonzentration der Teilnehmer in mmol/L in der rechten Spalte (dh Cholesterin, die abhängige Variable), wie unten gezeigt:
Veröffentlicht mit schriftlicher Genehmigung von StataCorp LP.,
Stata
Testverfahren in Stata
In diesem Abschnitt zeigen wir Ihnen, wie Sie Ihre Daten mithilfe der linearen Regression in Stata analysieren, wenn die sechs Annahmen im vorherigen Abschnitt, Annahmen, nicht verletzt wurden. Sie können eine lineare Regression mit Code oder der grafischen Benutzeroberfläche (GUI) von Stata durchführen. Nachdem Sie Ihre Analyse durchgeführt haben, zeigen wir Ihnen, wie Sie Ihre Ergebnisse interpretieren. Wählen Sie zunächst aus, ob Sie Code oder die grafische Benutzeroberfläche (GUI) von Stata verwenden möchten.,
Code
Der Code zur Durchführung einer linearen Regression Ihrer Daten hat folgende Form:
regress DependentVariable IndependentVariable
Dieser Code wird in das Feld eingegeben:
Veröffentlicht mit schriftlicher Genehmigung von StataCorp LP.,
In unserem Beispiel, in dem die abhängige Variable Cholesterin und die unabhängige Variable time_tv ist, lautet der erforderliche Code:
Regress Cholesterin time_tv
Hinweis 1: Sie müssen genau sein, wenn Sie den Code in das Feld eingeben. Der Code ist „Groß-und Kleinschreibung“. Zum Beispiel, wenn Sie „C“ eingegeben haben, wobei das “ C “ eher Groß als klein ist (dh, ein kleines „c“), was es sein sollte, erhalten Sie eine Fehlermeldung wie die folgende:
Hinweis 2: Wenn Sie immer noch die Fehlermeldung in Anmerkung 2 erhalten: Oben lohnt es sich, den Namen zu überprüfen, den Sie Ihren beiden Variablen im Dateneditor beim Einrichten Ihrer Datei gegeben haben (dh siehe den Dateneditorbildschirm oben)., Im Feld auf der rechten Seite des Dateneditorbildschirms schreiben Sie Ihre Variablen im Abschnitt
, nicht im Abschnitt
, den Sie in den Code eingeben müssen (siehe unten für unsere abhängige Variable). Dies mag offensichtlich erscheinen, aber es ist ein Fehler, der manchmal gemacht wird, was zu dem Fehler in Anmerkung 2 oben führt.
Daher geben sie den code, regress die time_tv, und drücken sie die“ Return/Enter “ taste auf ihre tastatur.,
Veröffentlicht mit schriftlicher Genehmigung von StataCorp LP.
Sie können die Stata-Ausgabe sehen, die hier erzeugt wird.,
Grafische Benutzeroberfläche (GUI)
Die drei Schritte zur Durchführung der linearen Regression in Stata 12 und 13 sind unten dargestellt:
- Klicken Sie auf Statistik > Lineare Modelle und verwandte > Lineare Regression im Hauptmenü, wie unten gezeigt:
Veröffentlicht mit schriftlicher Genehmigung von StataCorp LP.,
Das Dialogfenster Regresslineare Regression wird angezeigt:
Veröffentlicht mit schriftlicher Genehmigung von StataCorp LP.
- Wählen Sie aus dem Dropdown-Feld Abhängige Variable: und aus dem Dropdown-Feld Unabhängige Variablen: time_tv aus. Sie erhalten den folgenden Bildschirm:
Veröffentlicht mit schriftlicher Genehmigung von StataCorp LP.,
-
Klicken Sie auf die Schaltfläche
. Dadurch wird die Ausgabe generiert.
Stata
Ausgabe der linearen Regressionsanalyse in Stata
Wenn Ihre Daten assumption #3 (dh es gab eine lineare Beziehung zwischen Ihren beiden Variablen), #4 (dh es gab keine signifikanten Ausreißer), assumption #5 (dh Sie hatten Unabhängigkeit von Beobachtungen), assumption #6 (dh Ihre Daten zeigten Homoskedastizität) und assumption #7 (dh Sie hatten,(Fehler) ungefähr normal verteilt waren), die wir zuvor im Abschnitt Annahmen erläutert haben, müssen Sie nur die folgende lineare Regressionsausgabe in Stata interpretieren:
Veröffentlicht mit schriftlicher Genehmigung von StataCorp LP.,
Die Ausgabe besteht aus vier wichtigen Informationen: (a) Der R2-Wert (Zeile“R-Quadrat“) stellt den Anteil der Varianz in der abhängigen Variablen dar, der durch unsere unabhängige Variable erklärt werden kann (technisch ist dies der Anteil der Variation, der vom Regressionsmodell über das mittlere Modell hinaus berücksichtigt wird). R2 basiert jedoch auf der Stichprobe und ist eine positiv voreingenommene Schätzung des Anteils der Varianz der abhängigen Variablen, die durch das Regressionsmodell (dh, ist); (b) ein angepasster R2-Wert (Zeile“Adj R-squared“), der positive Verzerrungen korrigiert, um einen Wert bereitzustellen, der in der Population erwartet würde; (c) der F-Wert, Freiheitsgrade („F( 1, 98)“) und die statistische Signifikanz des Regressionsmodells („Prob > F“ row); und (d) die Koeffizienten für die konstante und unabhängige Variable („Coef. spalte), die die Informationen enthält, die Sie benötigen, um die abhängige Variable time_tv mithilfe der unabhängigen Variablen time_tv vorherzusagen.
In diesem Beispiel, R2 = 0.151. Angepasst R2 = 0,143 (bis 3 d. p.,), was bedeutet, dass die unabhängige Variable time_tv 14,3% der Variabilität der abhängigen Variablen Cholesterin in der Population erklärt. Das bereinigte R2 ist auch eine Schätzung der Effektgröße, die mit 0,143 (14,3%) nach Cohens (1988) Klassifikation auf eine mittlere Effektgröße hinweist. Normalerweise wird jedoch R2 nicht das angepasste R2 in den Ergebnissen gemeldet. In diesem Beispiel ist das Regressionsmodell statistisch signifikant, F (1, 98) = 17,47, p = .0001., Dies zeigt, dass das angewandte Modell insgesamt die abhängige Variable Cholesterin statistisch signifikant vorhersagen kann.
Hinweis: Wir präsentieren die Ausgabe aus der obigen linearen Regressionsanalyse. Da Sie Ihre Daten jedoch auf die zuvor im Abschnitt Annahmen erläuterten Annahmen getestet haben sollten, müssen Sie auch die Stata-Ausgabe interpretieren, die beim Testen auf diese Annahmen erstellt wurde. Dies beinhaltet: (a) die Scatterplots, mit denen Sie überprüft haben, ob eine lineare Beziehung zwischen Ihren beiden Variablen besteht (dh,, Annahme #3); (b) casewise Diagnose zu überprüfen es gab keine signifikanten Ausreißer (d.h., Annahme #4); (c) die Ausgabe von der Durbin-Watson-Statistik zu überprüfen, für die Unabhängigkeit der Beobachtungen (d.h., Annahme #5); (d) ein Streudiagramm der Residuen standardisierte Residuen gegen die regression der standardisierten vorhergesagten Wert, um zu bestimmen, ob Ihre Daten zeigten, homoskedastizität (d.h., Annahme #6); und ein Histogramm (mit überlagerter normalverteilungskurve) und Normal P-P Plot um zu überprüfen, ob die Residuen (Fehler) waren annähernd normal verteilt (D. H., Annahme #7)., Denken Sie auch daran, dass, wenn Ihre Daten eine dieser Annahmen nicht erfüllt haben, die Ausgabe, die Sie aus der linearen Regressionsverfahren (dh die Ausgabe, die wir oben diskutieren) erhalten, nicht mehr relevant ist und Sie möglicherweise einen anderen statistischen Test durchführen müssen, um Ihre Daten zu analysieren.,
Stata
Meldung der Ausgabe der linearen Regressionsanalyse
Wenn Sie die Ausgabe Ihrer linearen Regression melden, empfiehlt es sich, Folgendes einzuschließen: (a) eine Einführung in die von Ihnen durchgeführte Analyse; (b) Informationen über Ihre Stichprobe, einschließlich fehlender Werte; (c) den beobachteten F-Wert, Freiheitsgrade und Signifikanzniveau (dh den p-Wert); (d) den Prozentsatz der Variabilität in der abhängigen Variablen, der durch die unabhängige Variable erklärt wird (dh Ihr angepasstes R2 ); und (e) die Regressionsgleichung für Ihr Modell., Basierend auf den obigen Ergebnissen könnten wir die Ergebnisse dieser Studie wie folgt melden:
- Allgemein
Eine lineare Regression ergab, dass die tägliche Fernsehzeit die Cholesterinkonzentration statistisch signifikant vorhersagen konnte, F (1, 98) = 17.47, p = .Und die Zeit, die fürs Fernsehen aufgewendet wurde, machte 14,3% der erklärten Variabilität der Cholesterinkonzentration aus. Die Regressionsgleichung lautete: vorhergesagte Cholesterinkonzentration = -2.135 + 0.044 x (Fernsehzeit).,
Zusätzlich zur Meldung der Ergebnisse wie oben kann ein Diagramm verwendet werden, um Ihre Ergebnisse visuell darzustellen. Sie können dies beispielsweise mit einem Scatterplot mit Konfidenz-und Vorhersageintervallen tun (obwohl es nicht sehr üblich ist, das letzte hinzuzufügen). Dies kann es anderen erleichtern, Ihre Ergebnisse zu verstehen. Darüber hinaus können Sie Ihre lineare Regressionsgleichung verwenden, um Vorhersagen über den Wert der abhängigen Variablen basierend auf verschiedenen Werten der unabhängigen Variablen zu treffen., Während Stata diese Werte nicht als Teil des obigen linearen Regressionsverfahrens erzeugt, gibt es in Stata eine Prozedur, mit der Sie dies tun können.