Uno dei più grandi aspetti del Sudoku è che il gioco offre sfide coinvolgenti sia per il principiante, così come il giocatore di puzzle stagionato. Ogni volta che giocano un puzzle su misura per il loro livello di competenza, sia il principiante che il risolutore esperto di Sudoku dovranno mettere una buona quantità di pensiero e tecnica nel completare l’attività. Il loro approccio, però, potrebbe non essere lo stesso. Risolvere un difficile puzzle di Sudoku richiederà un insieme piuttosto diverso di tecniche rispetto a uno facile., Questo articolo presenta nove tali tecniche; in difficoltà crescente.
Quando si utilizzano queste tecniche, il modo in cui i professionisti preferiscono farlo, è quello di iniziare con quelli di base. Utilizzare le prime tecniche per inserire il maggior numero possibile di numeri. Poi, quando è possibile aggiungere non più numeri alla scheda utilizzando le tecniche di base, provare quelli più avanzati. Fai uno alla volta finché non puoi tracciare un altro numero in una cella. Quindi, iniziare nuovamente con le tecniche di base e ripetere il processo. Si dovrebbe essere in grado di risolvere quasi tutti i puzzle di Sudoku utilizzando queste tecniche.,
Tecniche per rimuovere i numeri:
Candidato unico
Quando una cella specifica può contenere solo un singolo numero, quel numero è un “candidato unico”. Ciò accade ogni volta che tutti gli altri numeri ma il numero candidato esiste nel blocco, nella colonna o nella riga corrente. In questo esempio, la cella rossa può contenere solo il numero 5, poiché gli altri otto numeri sono stati tutti utilizzati nel blocco, nella colonna e nella riga correlati.,
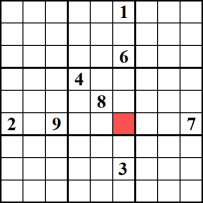
Candidato unico
Sai che ogni blocco, riga e colonna su una scheda Sudoku deve contenere ogni numero compreso tra 1 e 9. Pertanto, se un numero, ad esempio 4, può essere inserito in una singola cella all’interno di un blocco/colonna/riga, allora quel numero è garantito per adattarsi lì. Questo esempio illustra il numero 4 come candidato univoco per la cella contrassegnata in rosso.,
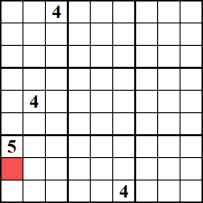
Tecniche per la rimozione dei candidati:
Blocco e colonna / Riga Interazione
Questo metodo, non vi aiuterà a matita in tutti i nuovi numeri ma si inchioda un numero in basso all’interno di una specifica riga o colonna. L’esempio mostra che il numero 7 può essere inserito solo nei globuli rossi della riga centrale. Quindi puoi rimuovere 7 come possibile candidato dal resto della riga.,
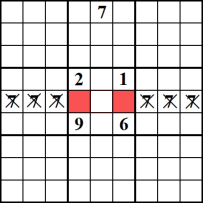
Interazione blocco / blocco
Questa tecnica è meglio compresa guardando l’esempio. Nel mezzo e nei blocchi medio-sinistra, il numero 8 deve essere posizionato in uno dei globuli rossi. Ciò significa che possiamo eliminare 8 dalle righe superiore e inferiore nella colonna centrale di destra.,
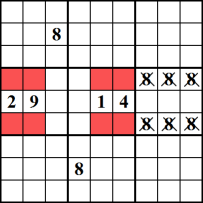
Sottoinsieme nudo
L’esempio mostra che la riga numero 1 e la riga numero 5 hanno entrambe una cella nella stessa colonna contenente solo i numeri candidati 4 e 7. Questi due numeri appaiono come candidati in tutte le altre celle aperte in quella colonna, ma poiché sono gli unici due candidati nelle righe 1 e 5, questi due numeri non possono apparire in nessun’altra parte della riga, quindi è possibile rimuoverli. Nell’esempio, le due coppie di candidati cerchiate in rosso, sono gli unici candidati., Poiché 4 e 7 devono essere collocati in una di queste due celle, tutte le coppie cerchiate in blu, possono rimuovere quei numeri come candidati. In questo puzzle, questo significa che 1 diventa unico candidato nella seconda riga; 2 diventa unico candidato nella riga 6; e quindi, 6 è unico candidato per la riga numero 4.
È inoltre possibile utilizzare questa tecnica se si dispone di più di due candidati. Ad esempio, diciamo che le coppie cerchiate in rosso erano invece candidati tripli dei numeri 1, 4, 7. Ciò significherebbe che quei tre numeri dovrebbero essere collocati nelle righe 1, 2 o 5., Potremmo rimuovere questi tre numeri come candidati in una qualsiasi delle celle rimanenti nella colonna. Questa tecnica funziona anche con quattro numeri candidati, supponendo che tu abbia 4 possibili candidati in quattro celle diverse in una riga / colonna.
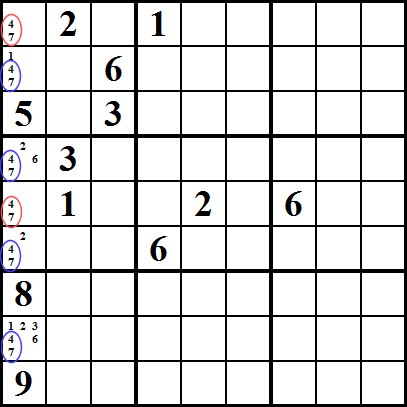
Sottoinsieme nascosto
Questo è simile al sottoinsieme Nudo, ma influisce sulle celle che contengono i candidati., In questo esempio, vediamo che i numeri 5, 6, 7 possono essere inseriti solo nelle celle 5 o 6 nella prima colonna (contrassegnato in un cerchio rosso) e che il numero 5 può essere inserito solo nella cella numero 8 (contrassegnato in un cerchio blu). Poiché 6 e 7 devono essere collocati in una delle celle con un cerchio rosso, ne consegue che il numero 5 deve essere posizionato nella cella numero 8, e quindi possiamo rimuovere eventuali altri candidati dall’ottava cella; in questo caso, 2 e 3.,
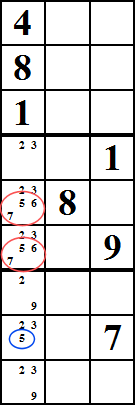
X-Wing
Questo metodo può funzionare quando si guardano le celle che comprendono un rettangolo, ad esempio le celle contrassegnate in rosso. In questo esempio, diciamo che le celle rosse e blu hanno tutte il numero 5 come numeri candidati. Ora, immagina se i globuli rossi sono le uniche celle nella colonna 2 e 8 in cui puoi inserire 5.
In questo caso devi ovviamente mettere un 5 in due dei globuli rossi, e sai anche che non possono essere entrambi nella stessa riga., Bene, ora, questo significa che puoi eliminare 5 come candidato per tutte le celle blu. Questo perché nella riga superiore, la prima o la seconda cella rossa devono avere un 5, e lo stesso si può dire della riga inferiore.
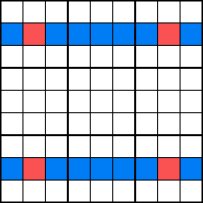
Swordfish
Swordfish è una versione più complicata di X-Wing. Nella maggior parte dei casi, la tecnica potrebbe sembrare molto lavoro per molto poco paga, ma alcuni enigmi possono essere risolti solo con esso. Quindi, se si vuole essere un maestro sudoku-solving, continuate a leggere!,
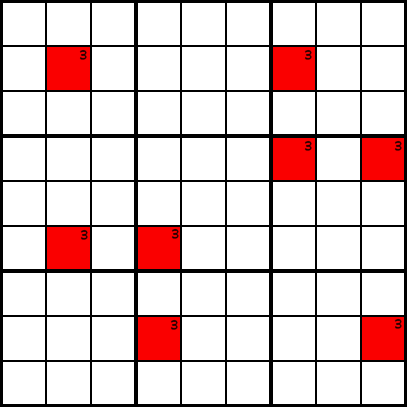Esempio ANell’esempio A, abbiamo tracciato alcune celle candidate per il numero 3. Ora, supponiamo che nelle colonne 2, 4, 7 e 9, le uniche celle che possono contenere il numero 3 siano quelle contrassegnate in rosso. Sai che ogni colonna deve contenere un 3.
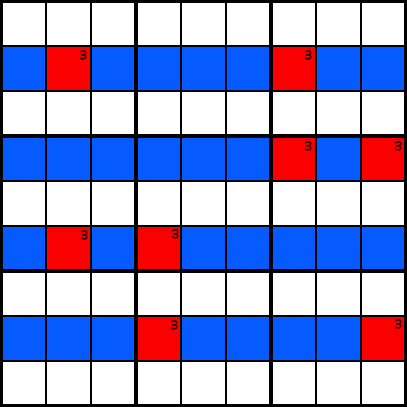Esempio B Guarda l’esempio B. Possiamo eliminare 3 come candidato in ogni cella contrassegnata in blu., La ragione di ciò è che se consideriamo i possibili posizionamenti del numero 3 nei globuli rossi, otteniamo due alternative: o devi mettere 3s nelle celle verdi, o nelle celle viola, come mostra l’esempio C. In ogni caso, ciascuna delle colonne 2, 4, 7 e 9, deve contenere un 3 in una delle celle colorate, quindi nessuna altra cella in quelle righe può contenere un 3.
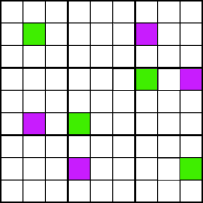Esempio CCome si riconosce un modello di pesce spada? Si cercano celle con numeri candidati comuni che possono essere concatenati insieme come nell’esempio D., Se inizi, ad esempio, la cella rossa in alto a sinistra. Quindi si disegna una linea verticalmente o orizzontalmente fino a raggiungere un’altra cella contenente lo stesso numero candidato. Quindi ripeti questo modello fino a quando non ritorni alla cella originale. Se si raggiunge la cella originale, si dispone di un modello di pesce spada!
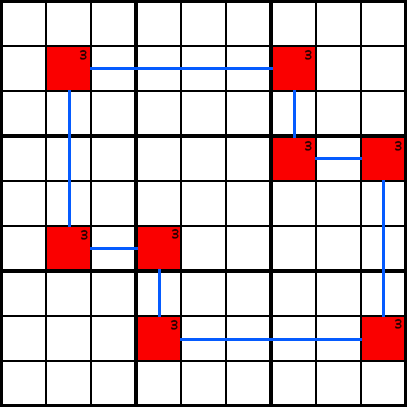Esempio D Forzare la catena
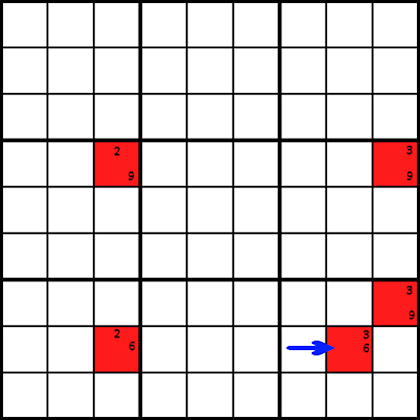
Forzare la catena può effettivamente aiutare a determinare esattamente quale numero deve contenere una determinata cella. Sfortunatamente, la tecnica non è la più facile da utilizzare., Guarda l’esempio qui sotto. Supponiamo che i candidati nei globuli rossi siano gli unici candidati per quelle cellule.
Forzare le catene funziona nel modo seguente: Inizia sulla cella rossa con la freccia rivolta verso di essa e compila uno dei due candidati, 3 o 6, per quella cella. Poi seguire e riempire il resto dei globuli rossi. Ora prendi nota dei valori immessi lungo la strada. Torna alla cella con cui hai iniziato e prova l’altro numero candidato per quella cella, e compila anche gli altri globuli rossi. Confronta i numeri che hai ora con il primo risultato., Potresti scoprire che in entrambi i casi, una determinata cella deve contenere un numero specifico.
In questo esempio, se metti il numero 3 nella cella iniziale, vedrai che la cella vicina in alto a destra deve contenere un 9. Ora, prova a inserire un 6 nella cella iniziale e muovi il contrario, inserendo i valori candidati. Quando raggiungi di nuovo la cella vicina in alto a destra, troverai che deve contenere anche un 9 questa volta. Quindi questa cella deve contenere un 9.
Questo è tutto., Spero che questo vi aiuterà a rompere anche i più difficili puzzle di sudoku là fuori. In bocca al lupo!
Questo articolo è una parte della nostra sezione di aiuto Sudoku.
Gioca Sudoku Epic
Sudoku Epic è un gioco di Sudoku gratuito di qualità premium ed è disponibile sulla maggior parte delle piattaforme: PC, Mac, iPhone, iPad, Android, Google Play Store e Amazon Appstore.
Sudoku Epic su Google Play
Sudoku Epic su iPhone/iPad