Assunzione di normalità della variabile dipendente
Il t-test indipendente richiede che la variabile dipendente sia approssimativamente distribuita normalmente all’interno di ciascun gruppo.
Nota: Tecnicamente, sono i residui che devono essere distribuiti normalmente, ma per un t-test indipendente, entrambi ti daranno lo stesso risultato.,
Puoi testarlo usando una serie di test diversi, ma il test di normalità Shapiro-Wilks o un metodo grafico, come un grafico Q-Q, sono molto comuni. È possibile eseguire questi test utilizzando le statistiche SPSS, la cui procedura può essere trovata nella nostra guida ai test per la normalità. Tuttavia, il t-test è descritto come un test robusto rispetto all’assunzione di normalità. Ciò significa che alcune deviazioni dalla normalità non hanno una grande influenza sui tassi di errore di tipo I. L’eccezione a questo è se il rapporto tra la dimensione del gruppo più piccola e più grande è maggiore di 1.,5 (più grande rispetto al più piccolo).
che Cosa fare quando si violano le ipotesi di normalità
Se si scopre che uno o entrambi del gruppo di dati non è circa distribuiti normalmente e dimensioni dei gruppi differiscono notevolmente, si hanno due opzioni: (1) trasformare i dati in modo che i dati vengono distribuiti normalmente (per fare questo in SPSS Statistics leggete la nostra guida su come Trasformare i Dati), o (2) eseguire il Mann-Whitney U test, è un test non parametrico che non richiede l’assunzione di normalità (per eseguire questo test in SPSS Statistics leggete la nostra guida sulla U di Mann-Whitney Test).,
Assunzione di omogeneità della varianza
Il test t indipendente presuppone che le varianze dei due gruppi che si stanno misurando siano uguali nella popolazione. Se le tue varianze sono disuguali, questo può influenzare il tasso di errore di tipo I. L’ipotesi di omogeneità della varianza può essere testata utilizzando il test di uguaglianza delle varianze di Levene, che viene prodotto nelle statistiche SPSS quando si esegue la procedura t-test indipendente., Se hai eseguito il test di Levene sull’uguaglianza delle varianze nelle statistiche SPSS, otterrai un risultato simile a quello riportato di seguito:

Questo test per l’omogeneità della varianza fornisce una statistica F e un valore di significatività (p-value). Ci occupiamo principalmente del valore di significatività-se è maggiore di 0,05 (cioè, p > .05), le nostre varianze di gruppo possono essere trattate come uguali. Tuttavia, se p < 0.05, abbiamo varianze disuguali e abbiamo violato l’assunzione di omogeneità delle varianze.,
il Superamento di una violazione dell’ipotesi di omogeneità della varianza
Se il Test di Levene di Uguaglianza delle Varianze è statisticamente significativo, che indica che il gruppo di varianze diverse della popolazione, è possibile correggere questa violazione non utilizzando il pool di stima per il termine di errore per la statistica t, ma utilizzando invece un adeguamento per i gradi di libertà con la Welch-Satterthwaite metodo., In tutta la realtà, probabilmente non avrai mai sentito parlare di queste regolazioni perché le statistiche SPSS nascondono queste informazioni e semplicemente etichettano le due opzioni come “Uguali varianze assunte” e “Uguali varianze non assunte” senza indicare esplicitamente i test sottostanti utilizzati., Tuttavia, si può vedere la prova di queste prove, come di seguito:
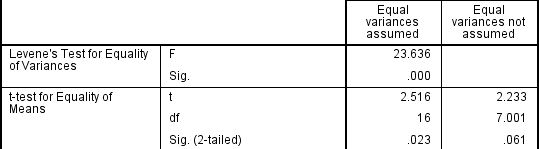
Dal risultato del Test di Levene di Uguaglianza delle Varianze, possiamo rifiutare l’ipotesi nulla che non vi è alcuna differenza in la varianza tra i gruppi e di accettare l’ipotesi alternativa che c’è una differenza statisticamente significativa della varianza tra i gruppi., L’effetto di non poter assumere uguali varianze è evidente nella colonna finale della figura precedente dove vediamo una riduzione del valore della statistica t e una grande riduzione dei gradi di libertà (df). Ciò ha l’effetto di aumentare il valore p al di sopra del livello di significatività critica di 0,05. In questo caso, non accettiamo quindi l’ipotesi alternativa e accettiamo che non ci siano differenze statisticamente significative tra i mezzi. Questa non sarebbe stata la nostra conclusione se non avessimo testato l’omogeneità delle varianze.